ML Aggarwal Mensuration Exe-18.1 Class 8 ICSE Ch-18 Maths Solutions. We Provide Step by Step Answer of Exe-18.1 Questions for Mensuration as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-8.
ML Aggarwal Mensuration Exe-18.1 Class 8 ICSE Maths Solutions
| Board | ICSE |
| Publications | Avichal Publishig Company (APC) |
| Subject | Maths |
| Class | 8th |
| Chapter-18 | Mensuration |
| Writer | ML Aggarwal |
| Book Name | Understanding |
| Topics | Solution of Exe-18.1 Questions |
| Edition | 2023-2024 |
Mensuration Exe-18.1
ML Aggarwal Class 8 ICSE Maths Solutions
Page-293
Question 1. The length and breadth of a rectangular field are in the ratio 9 : 5. If the area of the field is 14580 square metres, find the cost of surrounding the field with a fence at the rate of ₹3·25 per metre.
Answer:
Let the length = 9x and the breadth = 5x
Area = l × b ⇒ 14580 = 9x × 5x
⇒ 45x2 = 14580
∴ x2 = 14580/45 = 324 ⇒ x = √324
⇒ x = √18 x 18
or x = 18
Length = 9 × 18 = 162 m
Breadth = 5 × 18 = 90 m
Perimeter = 2(l + b)
= 2 (162 + 90) = 2(252)
= 504 m.
∴ Cost for 504 m fencing the surrounding
at the rate of ₹3·25 per metre = ₹(504 × 3·25) = ₹1638
Question 2. A rectangle is 16 m by 9 m. Find a side of the square whose area equals the area of the rectangle. By how much does the perimeter of the rectangle exceed the perimeter of the square?
Answer:
Area of rectangle = (16 × 9) m2 = 144 m2
Area of square = Area of rectangle (given)
∴ (side)2 = 144
Side =√144 = √12 x 12 = 12 m
Perimeter of square = 4 × 12 = 48 m
Perimeter of rectangle = 2(l + b) = 2 (16 + 9) = 50 m
Difference in their perimeters = 50 – 48 = 2 m
Question 3. Two adjacent sides of a parallelogram are 24 cm and 18 cm. If the distance between longer sides is 12 cm, find the distance between shorter sides.
Answer:
Taking 24 cm as a base of parallelogram, its height is 12 cm.
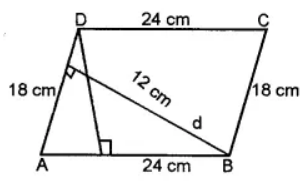
∴ Area of parallelogram = b × h = 24 × 12 = 288 cm2
Let d cm be the distance between the shortest sides.
∴ Area of parallelogram = (18 × d) cm2
⇒ 18 × d = 288
⇒ d = 288/18 = 16 cm
Question 4. Rajesh has a square plot with the measurement as shown in the given figure. He wants to construct a house in the middle of the plot. A garden is developed around the house. Find the total cost of developing a garden around the house at the rate of ₹50 per m2.
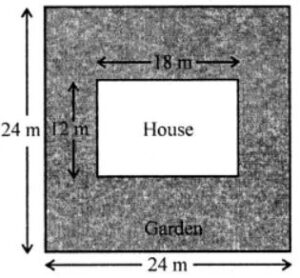
Answer:
Side of square plot = 24 m
Length of house (l) = 18 m
and breadth (b) = 12m

Now area of square plot = (24)2 m2 = 24 × 24 = 576 m2
and area of hosue = 18 × 12 = 216 m2
Remaining area of the garden = 576 – 216 = 360 m2
Cost of developing the garden = ₹50 per m2
Total cost = ₹50 × 360 = ₹18000
Question 5. A flooring tile has a shape of a parallelogram whose base is 18 cm and the corresponding height is 6 cm. How many such tiles are required to cover a floor of area 540 m2? (If required you can split the tiles in whatever way you want to fill up the comers).
Answer:
Base of the parallelogram-shaped flooring tile = 18 cm
and height = 6 cm
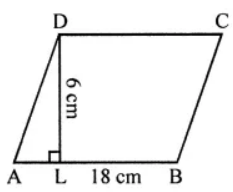
∴ Area of one tile = Base × Height = 18 × 6 = 108 cm2
Area of floor = 540 m2
∴ Number of tiles = Total area/Area of one title
= (540x100x100)/108 = 50000
Question 6. An ant is moving around a few food pieces of different shapes scattered on the floor. For which food piece would the ant have to take a longer round?
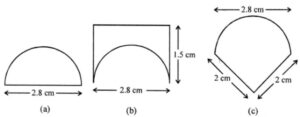
Answer:
(a) Diameter of semicircle = 2.8 cm
∴ Perimeter = πr + 2r
= 22/7 × 2.8 + 2 × 2.8
= 8.8 + 5.6 cm
= 14.4 cm
(b) Total perimeter = 1.5 + 1.5 + 2.8 + semi circumference (πr, where r = 2.8/2 = 1.4 cm)
= 1.5 + 1.5 + 2.8 + (22/7 x 1.4)
= 5.8 + 8.8
= 14.6 cm
(c) Total perimeter = 2 + 2 + Semi circumference (πr, where r = 2.8/2 = 1.4 cm)
= 4 + 8.8
= 12.8 cm
Therefore, it is clearly seen that distance of (b) i.e. 14.6 is the longest.
Mensuration Exe-18.1
ML Aggarwal Class 8 ICSE Maths Solutions
Page-294
Question 7. In the adjoining figure, the area enclosed between the concentric circles is 770 cm2. If the radius of the outer circle is 21 cm, calculate the radius of the inner circle.
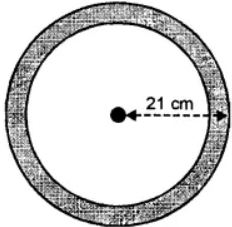
Answer:
Radius of outer circle (R) = 21 cm.
radius of inner circle (r) = r cm.
Area of shaded portion = 770 cm2
⇒ π (R2 – r2) = 770
⇒ 22/7 (212 – r2) = 770
⇒ 441 – r2 = 770 × 7/22 = 35 × 7 = 245
⇒ r2 = 441 – 245
⇒ r2 = 196
⇒ r2 = 196
⇒ r = √196 = √14 x 14
⇒ r = 14 cm
Question 8. A copper wire when bent in the form of a square encloses an area of 121 cm2. If the same wire is bent into the form of a circle, find the area of the circle.
Answer:
Area of the square = 121 cm2
∴ Side =√121 = √11 x 11 = 11 cm
Perimeter = 4 a = 4 × 11= 44 cm
Now, circumference of the circle = 44 cm
∴ Radius =(44 x 7)/(2 x 22) = 7cm
and area of the circle = πr2 = 22/7(7)2
= 22/7 × 7 × 7 = 154 cm2
Question 9. From the given figure, find
(i) the area of ∆ ABC
(ii) length of BC
(iii) the length of altitude from A to BC
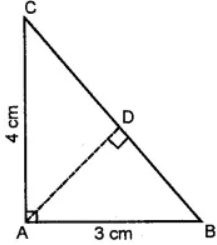
Answer:
(i) Base = 3 cm, height = 4 cm.
Area = 1/2 × base × height
= 1/2 × 3 × 4 = 6 cm2
(ii) By pythagoras theorem,
BC2 = AB2 + AC2
∴ BC2 = (3)2 + (4)2
= 9 + 16 = 25
⇒ BC =√25 cm = 5 cm
(iii) Now, Base = BC = 5 cm., h = AD = ?
Area = 1/2 × b × h
⇒ 6 = 1/2 × 5 × h
[∵ Area = 6 cm2 as in part (i)]
⇒ h = 12/5 = 2·4 cm.
(ML Aggarwal Mensuration Exe-18.1 Class 8 ICSE Maths )
Question 10. A rectangular garden 80 m by 40 m is divided into four equal parts by two cross-paths 2.5 m wide. Find
(i) the area of the cross-paths.
(ii) the area of the unshaded portion.

Answer:
Length of rectangular garden = 80 m
and breadth = 40 m
Width of crossing path 2.5 m

Area of length wise path
= 80 × 2.5 = 200 m2
Area of breadth wise path
= 40 × 2.5 = 100 m2
(i) Total area of both paths
= 200 + 100 – 2.5 × 2.5 m2
= 300 – 6.25 = 293.75 m2
(ii) Area of unshaded portion
= Area of garden – Area of paths
= 80 × 40 – 293.75 m2
= 3200 – 293.75 m2
= 2906.25 m2
Question 11. In the given figure, ABCD is a rectangle. Find the area of the shaded region.
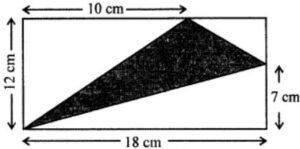
Answer:
In the given figure.
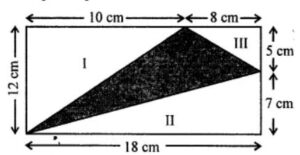
Length of rectangle = 18 cm
and breadth = 12 cm
∴ Area = l × b = 18 × 12 cm2 = 216 cm2
Area of triangle I = 1/2 × 12 × 10 = 60 cm2
Area of triangle III = 1/2 × 18 × 7 = 63 cm2
∴ Area of shaded portion
= Area of rectangle – Area of 3 triangles
= 216 – (60 + 63 + 20)
= 216 – 143 cm2
= 73 cm2
Question 12. In the adjoining figure, ABCD is a square grassy lawn of area 729 m2. A path of uniform width runs all around it. If the area of the path is 295 m2, find
(i) the length of the boundary of the square field enclosing the lawn and the path.
(ii) the width of the path.

Answer:
Area of square ABCD = 729 m2
Side =√729 = √27 x 27 = 27 m
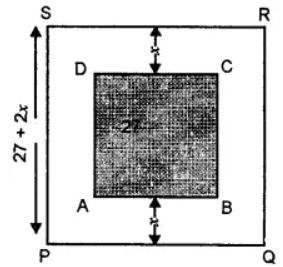
Let the width of path = x m
Then side of outer field = 27 + x + x = (27 + 2x) m
Area of square PQRS = (27 + 2x)2 m2
Area of PQRS – Area of ABCD = Area of path
∴ (27 + 2x)2 m2 – 729 m2 = 295 m2
⇒ 729 + 4x2 + 108x – 729 = 295
⇒ 4x2 + 108x – 295 = 0
![]()

∴ Width of the path is 2.5 m
Now, side of square field PQRS
= 27 + 2x = (27 + 2 × 2·5) m = 32 m
Length of boundary = 4 × side = 32 × 4 = 128
— End of Mensuration Exe-18.1 Class 8 ICSE Maths Solutions :–
Return to : – ML Aggarwal Maths Solutions for ICSE Class -8
Thanks



It’s a very nice website. I love it. Thank u ICSE HELP.COM
thanks you and keep in touch