ML Aggarwal Mid Point Theorem Exe-11 Class 9 ICSE Maths APC Understanding Solutions. Solutions of Exercise-11. This post is the Solutions of ML Aggarwal Chapter 11- Mid Point Theorem for ICSE Maths Class-9. APC Understanding ML Aggarwal Solutions (APC) Avichal Publication Solutions of Chapter-11 Mid Point Theorem for ICSE Board Class-9. Visit official website CISCE for detail information about ICSE Board Class-9.
ML Aggarwal Mid Point Theorem Exe-11 Class 9 ICSE Maths Solutions
| Board | ICSE |
| Publications | Avichal Publishig Company (APC) |
| Subject | Maths |
| Class | 9th |
| Chapter-11 | Mid Point Theorem |
| Writer | ML Aggarwal |
| Book Name | Understanding |
| Topics | Solution of Exe-11 Questions |
| Edition | 2021-2022 |
Exe-11 Solutions of ML Aggarwal for ICSE Class-9 Ch-11, Mid Point Theorem
Note:- Before viewing Solutions of Chapter -11 Mid Point Theorem Class-9 of ML Aggarwal Solutions . Read the Chapter Carefully. Then solve all example given in Exercise-11, MCQs, Chapter Test.
Mid Point Theorem Exe-11
ML Aggarwal Class 9 ICSE Maths Solutions
Page 237
Question 1.
(a) In the figure (1) given below, D, E and F are mid-points of the sides BC, CA and AB respectively of ∆ ABC. If AB = 6 cm, BC = 4.8 cm and CA= 5.6 cm, find the perimeter of
(i) the trapezium FBCE
(ii) the triangle DEF.
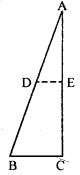
(b) In the figure (2) given below, D and E are mid-points of the sides AB and AC respectively. If BC =
5.6 cm and ∠B = 72°, compute
(i) DE
(ii)∠ADE.
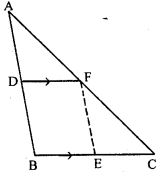
(c) In the figure (3) given below, D and E are mid-points of AB, BC respectively and DF || BC. Prove that DBEF is a parallelogram. Calculate AC if AF = 2.6 cm.
Answer :
(a)
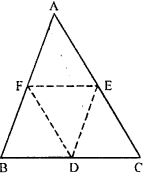
(i) Given : AB = 6 cm, BC = 4.8 cm, and CA = 5.6 cm
Required : The perimeter of trapezium FBCA.
F is the mid-point of AB
We know that, BF = ½ AB = ½ × 6 = 3 cm …(1)
It is given that
E is the mid-point of AC
CE = ½ AC = ½ × 5.6 = 2.8 cm …(2)
Here, F and E are the mid-point of AB and CA
FE || BC
FE = ½ BC = ½ × 4.8 = 2.4 cm …(3)
Here,
Perimeter of trapezium FBCE = BF + BC + CE + EF
Now substituting the value from all the equations
= 3 + 4.8 + 2.8 + 2.4
= 13 cm
Hence, the perimeter of trapezium FBCE is 13 cm.
(ii) D, E and F are the midpoints of sides BC, CA and AB of Δ ABC
Here EF || BC
EF = ½ BC = ½ × 4.8 = 2.4 cm
DE = ½ AB = ½ × 6 = 3 cm
FD = ½ AC = ½ × 5.6 = 2.8 cm
We know that
Perimeter of Δ DEF = DE + EF + FD
Substituting the values
= 3 + 2.4 + 2.8
= 8.2 cm
(b) It is given that
D and E are the mid-point of sides AB and AC
BC = 5.6 cm and ∠B = 72°
To find: (i) DE (ii) ∠ADE
In Δ ABC
D and E is the mid-point of the sides AB and AC
Using mid-point theorem
DE || BC
(i) DE = ½ BC = ½ × 5.6 = 2.8 cm
(ii) ∠ADE = ∠B are corresponding angles
It is given that
∠B = 72° and BC || DE
∠ADE = 72°
(c) It is given that, D and E are the midpoints of AB and BC respectively
DF || BC and AF = 2.6 cm
To find: (i) BEF is a parallelogram
(ii) Calculate the value of AC
Proof:
(i) In Δ ABC
D is the midpoint of AB and DF || BC
F is the midpoint of AC …(1)
F and E are the midpoints of AC and BC
EF || AB …(2)
Here DF || BC
DF || BE …(3)
Using equation (2)
EF || AB
EF || DB …(4)
Using equation (3) and (4)
DBEF is a parallelogram
(ii) F is the midpoint of AC
AC = 2×AF = 2× 2.6 = 5.2 cm
Mid Point Theorem Exe-11
ML Aggarwal Class 9 ICSE Maths Solutions
Page 238
Question 2. Prove that the four triangles formed by joining in pairs the mid-points of the sides c of a triangle are congruent to each other.
Answer :
In Δ ABC
D, E and F are the mid-points of AB, BC and CA
Now join DE, EF and FD
To find:
Δ ADF ≅ Δ DBE ≅ Δ ECF ≅ Δ DEF
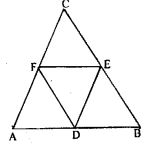
To prove:
In Δ ABC
D and E are the mid-points of AB and BC
DE || AC or FC
DF || EC
DECF is a parallelogram
Diagonal FE divides the parallelogram DECF in two congruent triangles DEF and CEF
Δ DEF ≅ Δ ECF …(1)
prove that,
Δ DBE ≅ Δ DEF …(2)
Δ DEF ≅ Δ ADF …(3)
Using equation (1), (2) and (3)
Δ ADF ≅ Δ DBE ≅ Δ ECF ≅ Δ DEF
Question 3. If D, E and F are mid-points of sides AB, BC and CA respectively of an isosceles triangle ABC, prove that ∆DEF is also F, isosceles.
Answer :
Given : ABC is an isosceles triangle in which AB = AC
D, E and F are the midpoints of the sides BC, CA and AB
Now D, E and F are joined
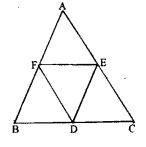
Find:
Δ DEF is an isosceles triangle
Proof:
D and E are the midpoints of BC and AC
Here DE || AB and DE = ½ AB …(1)
D and F are the midpoints of BC and AB
Here DF || AC and DF = ½ AC …(2)
AB = BC and DE = DF
Hence,
Δ DEF is an isosceles triangle.
Question 4. The diagonals AC and BD of a parallelogram ABCD intersect at O. If P is the mid-point of AD, prove that
(i) PQ || AB
(ii) PO=(1/2)CD.
Answer :
(i) Given : ABCD is a parallelogram in which diagonals AC and BD intersect each other. At point O, P is the mid-point of AD. Join OP.
To find: (i) PQ || AB (ii) PQ = ½ CD
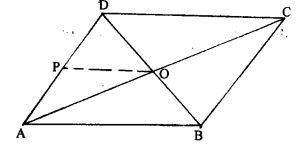
Proof:
(i) In parallelogram diagonals bisect each other
BO = OD
Here O is the mid-point of BD
In ΔABD,
P and O is the midpoint of AD and BD
PO || AB and PO = ½ AB …(1)
Hence,
it is proved that PO || AB.
(ii) ABCD is a parallelogram
AB = CD …(2)
Using both (1) and (2)
PO = ½ CD
Question 5. In the adjoining figure, ABCD is a quadrilateral in which P, Q, R and S are mid-points of AB, BC, CD and DA respectively. AC is its diagonal. Show that
(i) SR || AC and SR =AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
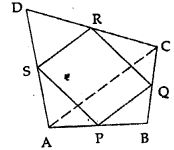
Answer :
In quadrilateral ABCD
P, Q, R and S are the mid-points of sides AB, BC, CD and DA
AC is the diagonal
Find:
(i) SR || AC and SR = ½ AC
(ii) PQ = SR
(iii) PQRS is a parallelogram
Proof:
(i) In Δ ADC
S and R are the mid-points of AD and DC
SR || AC and SR = ½ AC …(1) [Using the mid-point theorem]
(ii) In Δ ABC
P and Q are the midpoints of AB and BC
PQ || AC and PQ = ½ AC …(2)
Using equation (1) and (2)
PQ = SR and PQ || SR
(iii) PQ = SR and PQ || SR
Therefore, PQRS is a parallelogram.
Question 6. Show that the quadrilateral formed by joining the mid-points of the adjacent sides of a square, is also a square,
Answer :
A square ABCD in which E, F, G and H are mid-points of AB, BC, CD and DA
Join EF, FG, GH and HE.
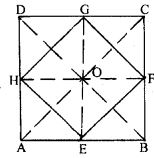
Find:
EFGH is a square
Construct AC and BD
Proof:
In Δ ACD
G and H are the mid-points of CD and AC
GH || AC and GH = ½ AC …(1)
In Δ ABC, E and F are the mid-points of AB and BC
EF || AC and EF = ½ AC …(2)
Using both equations
EF || GH and EF = GH = ½ AC …(3)
We can prove
EF || GH and EH = GF = ½ BD
The diagonals of square are equal
AC = BD
By dividing both sides by 2
½ AC = ½ BD …(4)
Using equation (3) and (4)
EF = GH = EH = GF …(5)
Hence, EFGH is a parallelogram
In Δ GOH and Δ GOF
OH = OF as the diagonals of parallelogram bisect each other
OG = OG is common
Using equation (5)
GH = GF
Δ GOH ≅ Δ GOF (SSS axiom of congruency)
∠GOH = ∠GOF (c.p.c.t)
∠GOH + ∠GOF = 180° as it is a linear pair
∠GOH + ∠GOH = 180°
2 ∠GOH = 1800
∠GOH = 180°/2 = 90°
So the diagonals of a parallelogram ABCD bisect and perpendicular to each other
Hence,
it is proved that EFGH is a square.
Question 7. In the adjoining figure, AD and BE are medians of ∆ABC. If DF U BE, prove that CF =  AC.
AC.
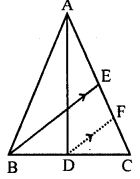
Answer :
AD and BE are the medians of Δ ABC
Construct DF || BE
Find:
CF = ¼ AC
Proof:
In Δ BCE
D is the mid-point of BC and DF || BE
F is the mid-point of EC
CF = ½ EC …(1)
E is the mid-point of AC
EC = ½ AC …(2)
Using both equations
CF = ½ EC = ½ (½ AC)
CF = ¼ AC
Hence proved.
Question 8.
(a) In the figure (1) given below, ABCD is a parallelogram. E and F are mid-points of the sides AB and CO respectively. The straight lines AF and BF meet the straight lines ED and EC in points G and H respectively. Prove that
(i) ∆HEB = ∆HCF
(ii) GEHF is a parallelogram.
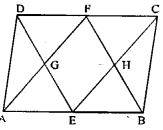
Answer :
ABCD is a parallelogram
E and F are the mid-points of sides AB and CD
To prove:
(i) Δ HEB = Δ HCF
(ii) GEHF is a parallelogram
Proof:
(i)
ABCD is a parallelogram
FC || BE
∠CEB = ∠FCE are alternate angles
∠HEB = ∠FCH …(1)
∠EBF = ∠CFB are alternate angles
∠EBH = ∠CFM …(2)
Here E and F are mid-points of AB and CD
BE = ½ AB …(3)
CF = ½ CD …(4)
We know that
ABCD is a parallelogram
AB = CD
Now dividing both sides by ½
½ AB = ½ CD
Using equation (3) and (4)
BE = CF …(5)
In Δ HEB and Δ HCF
∠HEB = ∠FCH (using equation 1)
∠EBH = ∠CFH (using equation 2)
BE = CF (using equation 5)
Δ HEB ≅ Δ HCF (ASA axiom of congruency)
Hence proved.
(ii)
E and F are the mid-points of AB and CD
AB = CD
AE = CF
Here AE || CF
AE = CF and AE || CF
So, AECF is a parallelogram.
G and H are the mid-points of AF and CE
GF || EH …(6)
In the same way we can prove that GFHE is a parallelogram
So G and H are the points on the line DE and BF
GE || HF …(7)
Using equation (6) and (7) GEHF is a parallelogram.
Hence proved.
Mid Point Theorem Exe-11
ML Aggarwal Class 9 ICSE Maths Solutions
Page 239
Question 9. ABC is an isosceles triangle with AB = AC. D, E and F are mid-points of the sides BC, AB and AC respectively. Prove that the line segment AD is perpendicular to EF and is bisected by it.
Answer :
ABC is an isosceles triangle with AB = AC
D, E and F are mid-points of the sides BC, AB and AC
Find:
AD is perpendicular to EF and is bisected by it.
Proof:
In Δ ABD and Δ ACD
ABC is an isosceles triangle
∠ABD = ∠ACD
D is the mid-point of BC
BD = BD
AB = AC (Given)
Δ ABD ≅ Δ ACD (SAS axiom of congruency)
∠ADB = ∠AOC (c. p. c. t)
∠ADB + ∠AOC = 180° is a linear pair
∠ADB + ∠ADB = 180°
By calculation
2 ∠ADB = 180°
∠ADB = 180°/2 = 90°
So AD is perpendicular to BC …(1)
D and E are the mid-points of BC and AB
DE || AF …(2)
D and F are the mid-points of BC and AC
EF || AD …(3)
Using equation (2) and (3)
AEDF is a parallelogram.
Here the diagonals of a parallelogram bisect each other
AD and EF bisect each other
Using equation (1) and (3)
EF || BC
So,
AD is perpendicular to EF
Hence proved.
Question 10.
(a) In the quadrilateral (1) given below, AB || DC, E and F are mid-points of AD and BD respectively. Prove that:
(i) G is mid-point of BC
(ii) EG = ½ (AB + DC)
(b) In the quadrilateral (2) given below, AB || DC || EG. If E is mid-point of AD prove that:
(i) G is the mid-point of BC
(ii) 2EG = AB + CD
(c) In the quadrilateral (3) given below, AB || DC.
E and F are mid-point of non-parallel sides AD and BC respectively. Calculate:
(i) EF if AB = 6 cm and DC = 4 cm.
(ii) AB if DC = 8 cm and EF = 9 cm.
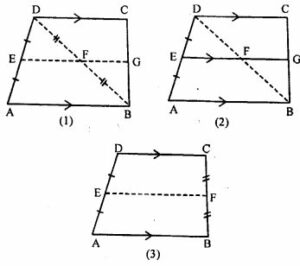
Answer :
(a) It is given that
AB || DC, E and F are mid-points of AD and BD
To prove:
(i) G is mid-point of BC
(ii) EG = ½ (AB + DC)
Proof:
(i) In Δ ABD
F is the mid-point of BD
DF = BF
E is the mid-point of AD
EF || AB and EF = ½ AB …(1)
AB || CD (Given)
EG || CD
F is the mid-point of BD
FG || DC
G is the mid-point of BC
(ii) FG = ½ DC …(2)
By adding both the equations
EF + FG = ½ AB + ½ DC
Taking ½ as common
EG = ½ (AB + DC)
Hence proved.
(b)
Quadrilateral ABCD in which AB || DC || EG
E is the mid-point of AD
To prove:
(i) G is the mid-point of BC
(ii) 2EG = AB + CD
Proof:
(i) AB || DC
EG || AB
EG || DC
In Δ DAB,
E is the mid-point of BD and EF = ½ AB …(1)
In Δ BCD,
F is the mid-point of BD and FG || DC
FG = ½ CD …(2)
By adding both equations
EF + FG = ½ AB + ½ CD
EG = ½ (AB + CD)
Hence proved.
(c)
A quadrilateral in which AB || DC
E and F are the mid-points of non-parallel sides AD and BC
To prove:
(i) EF if AB = 6 cm and DC = 4 cm.
(ii) AB if DC = 8 cm and EF = 9 cm.
Proof:
The length of line segment joining the mid-points of two non-parallel sides is half the sum of the lengths of the parallel sides
E and F are the mid-points of AD and BC
EF = ½ (AB + CD) …(1)
(i) AB = 6 cm and DC = 4 cm
Substituting in equation (1)
EF = ½ (6 + 4)
By calculation
EF = ½ × 10 = 5 cm
(ii) DC = 8 cm and EF = 9 cm
Substituting in equation (1)
EF = ½ (AB + DC)
By calculation
9 = ½ (AB + 8)
⇒ 18 = AB + 8
18 – 8 = AB
⇒ AB = 10 cm
Question 11.
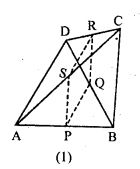
(a) In the quadrilateral (1) given below, AD = BC, P, Q, R and S are mid-points of AB, BD, CD and AC respectively. Prove that PQRS is a rhombus.
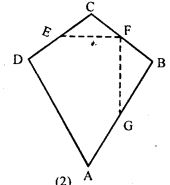
(b) In the figure (2) given below, ABCD is a kite in which BC = CD, AB = AD, E, F, G are mid-points of CD, BC and AB respectively. Prove that:
(i) ∠EFG = 90
(ii) The line drawn through G and parallel to FE bisects DA.
Answer :
(a)
A quadrilateral ABCD in which AD = C
P, Q, R and S are mid-points of AB, BD, CD and AC
To prove:
PQRS is a rhombus

Proof:
(i) In Δ ABD
P and Q are mid points of AB and BD
PQ || AD and PQ = ½ AB …(1)
In Δ BCD,
R and Q are mid points of DC and BD
RQ || BC and RQ = ½ BC …(2)
P and S are mid-points of AB and AC
PS || BC and PS = ½ BC …(3)
AD = BC
PS || RQ and PQ = PS = RQ
Here, PS || RQ and PS = RQ
PQRS is a parallelogram
PQ = RS = PS = RQ
PQRS is a rhombus
Hence proved.
(ii) ABCD is a kite in which BC = CD, AB = AD, E, F, G are mid-points of CD, BC and AB

To prove:
(i) ∠EFG = 90°
(ii) The line drawn through G and parallel to FE bisects DA
Join AC and BD
Construct GH through G parallel to FE
Proof:
(i)
Diagonals of a kite interest at right angles
∠MON = 90° …(1)
In Δ BCD
E and F are mid-points of CD and BC
EF || DB and EF = ½ DB …(2)
EF || DB
MF || ON
∠MON + ∠MFN = 180°
⇒ 90° + ∠MFN = 180°
By calculation
∠MFN = 180° – 90° = 90°
So, ∠EFG = 90°
Hence proved.
(ii) In Δ ABD
G is the mid-point of AB and HG || DB
Using equation (2)
EF || DB and EF || HG
HG || DB
Here, H is the mid-point of DA
Hence,
The line drawn through G and parallel to FE bisects DA.
Question 12. In the adjoining figure, the lines l, m and n are parallel to each other, and G is mid-point of CD. Calculate:
(i) BG if AD = 6 cm
(ii) CF if GE = 2.3 cm
(iii) AB if BC = 2.4 cm
(iv) ED if FD = 4.4 cm.

Answer :
The straight line l, m and n are parallel to each other
G is the mid-point of CD
Find:
(i) BG if AD = 6 cm
(ii) CF if GE = 2.3 cm
(iii) AB if BC = 2.4 cm
(iv) ED if FD = 4.4 cm

Proof:
(i) In Δ ACD,
G is the mid-point of CD
BG || AD as m || n
Here B is the mid-point of AC and BG = ½ AD
BG = ½ × 6 = 3 cm
(ii) In Δ CDF
G is the mid-point of CD
GE || CF as m || l
Here E is the mid-point of DF and GE = ½ CF
CF = 2GE
CF = 2 ×2.3 = 4.6 cm
(iii) From (i)
B is the mid-point of AC
AB = BC
BC = 2.4 cm
So AB = 2.4 cm
(iv) From (ii)
E is the mid-point of FD
ED = ½ FD
FD = 4.4 cm
⇒ ED = ½ × 4.4 = 2.2 cm
Hence proved.
— : End of ML Aggarwal Mid Point Theorem Exe-11 Class 9 ICSE Maths Solutions :–
Return to :- ML Aggarawal Maths Solutions for ICSE Class-9
Thanks
Please Share with Your Friends