ML Aggarwal Linear Equations and Inequalities in One Variable Exe-12.2 Class 8 ICSE Ch-12 Maths Solutions. We Provide Step by Step Answer of Exe-12.2 Questions for Linear Equations and Inequalities in One Variable as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-8.
ML Aggarwal Linear Equations and Inequalities in One Variable Exe-12.2 Class 8 ICSE Maths Solutions
| Board | ICSE |
| Publications | Avichal Publishig Company (APC) |
| Subject | Maths |
| Class | 8th |
| Chapter-12 | Linear Equations and Inequalities in One Variable |
| Writer | ML Aggarwal |
| Book Name | Understanding |
| Topics | Solution of Exe-12.2 Questions |
| Edition | 2023-2024 |
Linear Equations and Inequalities in One Variable Exe-12.2
ML Aggarwal Class 8 ICSE Maths Solutions
Page-213
Question 1. Three more than twice a number is equal to four less than the number. Find the number.
Answer:
Let the number = x
Twice the number = 2x
According to problem, 3 + 2x = x – 4
⇒ 3 + 2x + 4 = x
⇒ 7 = x – 2x
⇒ 7 = -x
⇒ -x = 7
⇒ x = -7
Hence, the number = -7
Question 2. When four consecutive integers are added, the sum is 46. Find the integers.
Answer:
Let x be the first integer, then the next
three consecutive integers are x + 1, x + 2 and x + 3
According to problem,
x + (x + 1) + (x + 2) + (x + 3) = 46
⇒ x + x + 1 + x + 2 + x + 3 = 46
⇒ 4x + 6 = 46
⇒ 4x = 46 – 6
⇒ 4x = 40
⇒ x = 40/4 = 10
Hence four consecutive integers are 10, (10 + 1), (10 + 2) and (10 + 3)
i.e. 10, 11, 12 and 13
Question 3. Manjula thinks a number and subtracts 7/3 from it. She multiplies the result by 6. The result now obtained is 2 less than twice the same number she thought of. What is the number?
Answer:
Let a number thought by Manjula = x
According to the condition,
(x – 7/3) × 6 = 2x – 2
⇒ 6x – 14 = 2x – 2
⇒ 6x – 2x = -2 + 14 = 12
⇒ 4x = 12
⇒ x = 12/4 = 3
Flence required number = 3
Question 4. A positive number is 7 times another number. If 15 is added to both the numbers, then one of the new number becomes 5/2 times the other new number. What are the numbers?
Answer:
Let the required number be x
Then the other number = x / 7
x + 15 = 5 / 2 {(x / 7) + 15}
2 (x + 15) = (5x / 7) + (5 × 15)
2x + 30 = (5x / 7) + 75
2x – (5 / 7) x = 75 – 30
{(14 – 5) / 7}x = 45
9x / 7 = 45
x = 45 × 7 / 9
We get,
x = 35
One number = 35
Other number = 35 / 7 = 5
Therefore, the numbers are 35 and 5
(ML Aggarwal Linear Equations and Inequalities in One Variable Exe-12.2 Class 8 )
Question 5. When three consecutive even integers are added, the sum is zero. Find the integers.
Answer:
Let the first even integer be x,
then next two consecutive even integers are (x + 2) and (x + 4)
According to given problem,
x + (x +2) + (x + 4) = 0
⇒ x + x + 2 + x + 4 =0
⇒ 3x + 6 = 0
⇒ 3x = – 6
⇒ x = -6/3
⇒ x = — 2
Hence three consecutive integers are -2, – 2 + 2, – 2 + 4 i.e. – 2, 0, 2
Question 6. Find two consecutive odd integers such that two-fifth of the smaller exceeds two-ninth of the greater by 4.
Answer:
Let the first odd integer = x
Then next consecutive odd integers = (x + 2)
(2 / 5) (x) = (2 / 9) (x + 2) + 4
2x / 5 = {2 (x + 2)} / 9 + 4
(2x / 5) – {2 (x + 2)} / 9 = 4
{18x – 10 (x + 2)} / 45 = 4
(18x – 10x – 20) / 45 = 4
(8x – 20) / 45 = 4
8x – 20 = 4 × 45
8x – 20 = 180
8x = 180 + 20
8x = 200
x = 200 / 8
x = 25
So, two consecutive odd integers are x = 25 and
(x + 2) = (25 + 2) = 27
Hence, two consecutive odd integers are 25 and 27
(ML Aggarwal Linear Equations and Inequalities in One Variable Exe-12.2 Class 8 )
Question 7. The denominator of a fraction is 1 more than twice its numerator. If the numerator and denominator are both increased by 5, it becomes 3/5. Find the original fraction.
Answer:
Let the numerator of the original fraction = x
Then, its denominator = 2x + 1
Hence,
The fraction = x / (2x + 1)
(x + 5) / {(2x + 1) + 5} = 3 / 5
(x + 5) / (2x + 1 + 5) = 3 / 5
5 (x + 5) = 3 (2x + 6)
5x + 25 = 6x + 18
5x – 6x = 18 – 25
-x = – 7
x = 7
Original fraction = x / (2x + 1)
= 7 / {2 (7) + 1}
= 7 / (14 + 1)
= 7 / 15
Therefore, the original fraction is 7 / 15
Question 8. Find two positive numbers in the ratio 2 : 5 such that their difference is 15.
Answer:
Let the two numbers be 2x and 5x
Because the ratio of these two numbers = 2x / 5x
= 2 / 5
= 2: 5
5x – 2x = 15
3x = 15
x = 15 / 3
x = 5
So, the numbers are 2x = 2 × 5 = 10 and 5x = 5 × 5 = 25
Hence, the required numbers are 10 and 25
Question 9. What number should be added to each of the numbers 12, 22, 42 and 72 so that the resulting numbers may be in proportion ?
Answer:
Let x be the required number
(12 + x), (22 + x), (42 + x) and (72 + x) are in proportion
(12 + x) / (22 + x) = (42 + x) / (72 + x)
On cross multiplication,
(12 + x) (72 + x) = (42 + x) (22 + x)
12 (72 + x) + x (72 + x) = 42 (22 + x) + x (22 + x)
864 + 12x + 72x + x2 = 924 + 42x + 22x + x2
864 + 84x + x2 = 924 + 64x + x2
864 + 84x + x2 – 924 – 64x – x2 = 0
864 + 84x – 64x – 924 = 0
84x – 64x = 924 – 864
20x = 60
x = 60 / 20
x = 3
Hence, the required number is 3
Question 10. The digits of a two-digit number differ by 3. If the digits are interchanged and the resulting number is added to the original number, we get 143. What can be the original number?
Answer:
Let one’s digit of a 2-digit number = x
Then ten’s digit = x + 3
∴ Number = x + 10(x + 3) = x + 10x + 30 = 11x + 30
By interchanging the digits,
One’s digit of new number = x + 3
and ten’s digit = x
∴ Number = x + 3 + 10x = 11x + 3
According to the condition,
11x + 30+ 11x + 3 = 143
⇒ 22x + 33 = 143
⇒ 22x = 143-33 = 110
⇒ x = 110/22 = 5
∴ Original number = 11x+ 30 = 11 × 5 + 30 = 55 + 30 = 85
(ML Aggarwal Linear Equations and Inequalities in One Variable Exe-12.2 Class 8 )
Question 11. Sum of the digits of a two-digit number is 11. When we interchange the digits, it is found that the resulting new number is greater than the original number by 63. Find the two-digit number.
Answer:
Sum of two digits of a 2-digit number = 11
Let unit’s digit of a 2-digit number = x
Then ten’s digit = 11 – x
∴ Number = x + 10(11 – x) = x + 110 – 10x = 110 -9x
By interchanging the digit,
One’s digit of new number = 11 – x
and ten’s digit = x
∴ Number = 11 – x + 10x = 11 + 9x
According to the condition,
11 + 9x – (110 – 9x) = 63
11 + 9x – 110 + 9x = 63
18x = 63 – 11 + 110 = 162
x = 162/18 = 9
∴ Original number = 110 – 9x = 110 – 9 × 9 = 110 – 81
= 29
Linear Equations and Inequalities in One Variable Exe-12.2
ML Aggarwal Class 8 ICSE Maths Solutions
Page-214
Question 12. Ritu is now four times as old as his brother Raju. In 4 years time, her age will be twice of Raju’s age. What are their present ages?
Answer:
Let the age of Raju = x years
then the age of Ritu = 4 × x years = 4x years
In 4 years time,
age of Raju = (x +4) years
age of Ritu = (4x + 4) years
According to given problem,
4x + 4 = 2 (x + 4)
⇒ 4x + 4 = 2x + 8
⇒ 4x – 2x = 8 – 4
⇒ 2x = 4 ⇒ x = 4/2
⇒ x = 2
Hence, the age of Raju = 2 years
and the age of Ritu = 4 × 2 years = 8 years.
Question 13. A father is 7 times as old as his son. Two years ago, the father was 13 times as old as his son. How old are they now?
Answer:
Let the present age of son = x years
Then, age of his father = 7 × x years = 7x years
Two years ago age of son = (x – 2) years
Two years ago age of his father = (7x – 2) years
According to given problem,
7x – 2 = 13 (x – 2)
⇒ 7x – 2 = 13x – 26
⇒ 7x – 13x = -26 + 2
⇒ -6x = -24
⇒ x = -24/-6
⇒ x = 4
Hence, age of son = 4 years
and age of his father = 7 × 4 years = 28 years.
(ML Aggarwal Linear Equations and Inequalities in One Variable Exe-12.2 Class 8 )
Question 14. The ages of Sona and Sonali are in the ratio 5 : 3. Five years hence, the ratio of their ages will be 10 : 7. Find their present ages.
Answer:
Ratio of ages of Sona and Sonali = 5: 3
Let us consider the present age of Sona and Sonali be 5x and 3x years respectively
Five years hence,
The age of Sona = 5x + 5 and
The age of Sonali = 3x + 5
(5x + 5) / (3x + 5) = 10 / 7
On cross multiplication,
7 (5x + 5) 10 (3x + 5)
35x + 35 = 30x + 50
35x – 30x = 50 – 35
5x = 15
x = 15 / 5
x = 3
Present age of Sona = 5x = 5 × 3 = 15 years and
Present age of Sonali = 3x = 3 × 3 = 9 years
Hence, the present age of Sona and Sonali is 15years and 9 years
Question 15. An employee works in a company on a contract of 30 days on the condition that he will receive ₹200 for each day he works and he will be fined ₹20 for each day he is absent. If he receives ₹3800 in all, for how many days did he remain absent?
Answer:
Period of contract = 30 days
If an employees works a day, he will get ₹200
If he is absent, he will be fined ₹20 per day
At the end of contract period, he get ₹3800
Let he remained absent for x days
Then he worked for = (30 – x) days
According to the condition,
(30 – x) × 200 – x × 20 = 3800
⇒ 6000 – 200x – 20x = 3800
⇒ 220x = 6000 – 3800 = 2200
⇒ x = 2200/220 = 10
He remained absent for 10 days.
Question 16. I have a total of ₹300 in coins of denomination ₹1, ₹2 and ₹5. The number of coins is 3 times the number of ₹5 coins. The total number of coins is 160. How many coins of each denomination are with me?
Answer:
Amount of coins = ₹300
and total coins = 160
Let number of coins of ₹5 = x
Then number of coins of ₹2 = 3x
and number of coins of ₹1 = 150 – (x + 3x) = 150 – 4x
According to the condition,
(160 – 4x) × 1 + 3x × 2 + x × 5 = 300
⇒ 160 – 4x + 6x + 5x = 300 ⇒ 160 + 7x = 300
⇒ 7x = 300 – 160 = 140
⇒ x = 140/7 = 20
∴ 5 rupee coins = 20
2 rupee coins = 3 × 20 = 60
and 1 rupee coins = 160 – 60 – 20 = 80
(ML Aggarwal Linear Equations and Inequalities in One Variable Exe-12.2 Class 8 )
Question 17. A local bus is carrying 40 passengers, some with ₹5 tickets and the remaining with ₹7.50 tickets. If the total receipts from these passengers is ₹230, find the number of passengers with ₹5 tickets.
Answer:
Let the number of passengers with ₹5 tickets = x
Then, the number of passengers with ₹7.50 tickets = (40 – x)
According to given problem,
5 × x + (40 – x) × 7.50 = 230
⇒ 5x + 300 – 7.5x = 230
⇒ 5x – 7.5x = 230 – 300
⇒ -2.5x = -70
⇒ x = 70/2.5 = 28
Hence, the number of passengers with ₹5 tickets = 28.
Question 18. On a school picnic, a group of students agree to pay equally for the use of a full boat and pay ₹10 each. If there had been 3 more students in the group, each would have paid ₹2 less. How many students were there in the group ?
Answer:
Let, the number of students in a group = x
when 3 students are more then,
the total number of students in the group = x + 3
According to given problem,
⇒ 10 × x = (x + 3) × (10 – 2)
⇒ 10x = (x + 3) × 8
⇒ 10x = 8 (x + 3)
⇒ 10x = 8x + 24
⇒ 10x – 8x = 24
⇒ 2x = 24
⇒ x = 24/2
⇒ x = 12
Hence, the number of students in the group = 12
Question 19. Half of a herd of deer are grazing in the field and three-fourths of the remaining are playing nearby. The rest 9 are drinking water from the pond. Find the number of deer in the herd.
Answer:
Let the number of deer in the herd = x
Number of deer grazing in the field = x / 2
Remaining = x – (x / 2)
= x / 2
Given that the (3 / 4) of the remaining deer are playing
= (3 / 4) × (1 / 2) x
= (3 / 8) x
Rest of deer = (x / 2) – (3 / 8) x
= (1 / 8) x
(1 / 8) x = 9
x = 9 × 8
x = 72
Therefore, total number of deer in the herd = 72
Question 20. Sakshi takes some flowers in a basket and visits three temples one by one. At each temple, she offers one half of the flowers from the basket. If she is left with 6 flowers at the end, find the number of flowers she had in the beginning.
Answer:
Let the total number of flowers in the basket = x
Flowers offered in first temple = x / 2
Remaining flowers = x – (x / 2)
= (x / 2)
Flowers offered in the second temple
(x / 2) × (1 / 2) = x / 4
Remaining flowers = (x / 2) – (x / 4)
= (x / 4)
Flowers offered in the third temple = (x / 4) × (1 / 2)
= (x / 8)
Remaining flowers = (x / 4) – (x / 8)
= (x / 8)
(x / 8) = 6
x = 6 × 8
x = 48
Hence, number of flowers she had in the beginning = 48
Question 21. Two supplementary angles differ by 50°. Find the measure of each angle.
Answer:
Let the angle be x
Then, its supplementary angle = 180° – x
According to given problem,
x – (180° – x) = 50°
⇒ x – 180° + x = 50°
⇒ 2x – 180° = 50°
⇒ 2x = 180° + 50°
⇒ 2x = 230°
⇒ x = 230°/2
⇒ x = 115°
Hence, the measurement of each angle be 115° and (180° – 115°)
i.e. 115° and 65°.
Question 22. If the angles of a triangle are in the ratio 5 : 6 : 7, find the angles.
Answer:
Let the angles of a triangle are 5x, 6x, and 7x
Then, we know that,
5x + 6x + 7x = 180°
⇒ 18x = 180°
⇒ x = 180°/18
⇒ x= 10°
Hence, the angle of a triangle are 5 × 10°, 6 × 10°,
and 7 × 10° i.e. 50°, 60° and 70°.
(ML Aggarwal Linear Equations and Inequalities in One Variable Exe-12.2 Class 8 )
Question 23. Two equal sides of an isosceles triangle are 3x – 1 and 2x + 2 units. The third side is 2x units. Find x and the perimeter of the triangle.
Answer:
Two equal sides of an isosceles triangle are 3x – 1 and 2x + 2
i. e. 3x – 1 = 2x + 2
⇒ 3x – 2x = 2 + 1
⇒ x = 3
Third side of triangle = 2x = 2 × 3 = 6 units
equal sides of an triangle = 3 × 3 – 1= 9 – 1 = 8 units
∴ Perimeter of the triangle = (8 + 8 + 6) units = 22 units
Question 24. If each side of a triangle is increased by 4 cm, the ratio of the perimeters of the new triangle and the given triangle is 7 : 5. Find the perimeter of the given triangle.
Answer:
Let the perimeter of original triangle be x cm
If each side of a triangle is increased by 4, then,
The perimeter will be = x + 4 × 3
= (x + 12) cm
Ratio of perimeter of new triangle and given triangle = 7: 5
(x + 12) / x = 7 / 5
On cross multiplication,
5 (x + 12) = 7x
5x + 60 = 7x
7x – 5x = 60
2x = 60
x = 60 / 2
x = 30
Hence, the perimeter of the given triangle is 30 cm
Question 25. The length of a rectangle is 5 cm less than twice its breadth. If the length is decreased by 3 cm and breadth increased by 2 cm, the perimeter of the resulting rectangle is 72 cm. Find the area of the original rectangle.
Answer:
Let, the breath of the original rectangle = x cm
Then, length of the original rectangle = (2x – 5) cm
When, length is decreased by 3 cm then new length
= [(2x – 5) – 3)] cm = (2x – 8) cm
When breadth is increased by 2 cm,
then new length = (x + 2) cm
New perimeter=2(new length + new breadth)
= 2 [(2x – 8) + (x + 2)]
= 2 [2x – 8 + x + 2]
= 2 (3x – 6) = 6x – 12
According to the given problem,
6x – 12 = 72
⇒ 6x = 72 + 12
⇒ 6x = 84
⇒ x = 84/6
⇒ x = 14
Breadth of the original rectangle = 14 cm
and length of the original rectangle = (2 × 14 – 5) cm = 23 cm
Area of the original rectangle = Length × Breadth
= 23 × 14 cm2 = 322 cm2
Question 26. A rectangle is 10 cm long and 8 cm wide. When each side of the rectangle is increased by x cm, its perimeter is doubled. Find the equation in x and hence find the area of the new rectangle.
Answer:
Length of rectangle (l) = 10 cm
and width (b) = 8 cm
Perimeter = 2(l + b) = 2(10 + 8) cm = 2 × 18 = 36 cm
By increasing each side by x cm
Then perimeter = 2[10 + x + 8 + x]
= 2(18 + 2x) = (36 + 4x) cm
According to the condition,
36 + 4x = 2(36)
⇒ 36 + 4x = 72
⇒ 4x = 72 – 36 = 36
⇒ x = 36/4
⇒ x = 9
Length of new rectanlge = l + x = 10 + 9 = 19 cm
and breadth = b + x = 8 + 9 = 17 cm
Area = Length x Breadth = 19 × 17 cm2 = 323 cm2
Question 27. A steamer travels 90 km downstream in the same time as it takes to travel 60 km upstream. If the speed of the stream is 5 km/hr, find the speed of the streamer in still water.
Answer:
Let the speed of the steamer = x km/ h
The speed downstream = (x + 5) km/h and
The speed upstream = (x – 5) km/ h
90 / (x + 5) = 60 / (x – 5)
On cross multiplication, we get,
90 (x – 5) = 60 (x + 5)
90x – 450 = 60x + 300
90x – 60x = 300 + 450
30x = 750
x = 750 / 30
x = 25
Hence, the speed of the streamer in still water is 25 km/ h
(ML Aggarwal Linear Equations and Inequalities in One Variable Exe-12.2 Class 8 )
Question 28. A steamer goes downstream and covers the distance between two ports in 5 hours while it covers the same distance upstream in 6 hours. If the speed of the stream is 1 km/h, find the speed of the streamer in still water and the distance between two ports.
Answer:
Speed of the stream in still water = 1 km/h
Let speed of streamer = x km/h
∴ It down speed = (x + 1) km/h
and up speed = (x – 1) km/h
According to the condition,
(x + 1) × 5 = (x – 1) × 6
⇒ 5x + 5 = 6x – 6
⇒ 6x – 5x = 5 + 6
⇒ x = 11
∴ Speed of streamer in still water = 11 km/h
and distance between two points = (11 + 1) × 5 = 60 km/h
Linear Equations and Inequalities in One Variable Exe-12.2
ML Aggarwal Class 8 ICSE Maths Solutions
Page-215
Question 29. Distance between two places A and B is 350 km. Two cars start simultaneously from A and B towards each other and the distance between them after 4 hours is 62 km. If the speed of one car is 8 km/h less than the speed of other cars, find the speed of each car.
Answer:
Distance between two places A and B = 350 km
Let the speed of car C1 = x km/h and
Speed of car C2 = (x – 8) km/h
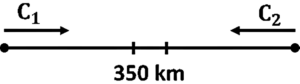
After 4 hours, the distance between two cars is 62 km
Hence,
x × 4 + (x – 8) × 4 = 350 – 62
4x + 4x – 32 = 288
8x = 288 + 32
8x = 320
x = 320 / 8
x = 40
Hence, speed of car C1 = 40 km/h
Speed of car C2 = (x – 8) = (40 – 8) = 32 km/h
Question 30. Nine person went to a hotel to take their dinner. Eight of them spent ₹60 each for the dinner and the ninth person spent ₹40 more than the averages expenditure of all the nine. How much money was spent by all of them?
Answer:
8 persons spent Rs. 60 each for their meals.
So the total money spent by 8 persons = 8*60 = 480
Suppose that the ninth person spent = x
So the total money spent by 9 persons = 480+x
Average of the money spent by 9 persons = (480+x)/9
As per question, the ninth one spent Rs., 40 more than the average expenditure of all the nine. So…
x = (480+x)/9+40
x = 480/9+x/9+40
x-x/9 = 480/9+40
(9x-x)/9 = (480+360)/9
8x/9 = 840/9
x = (840/9)*(9/8)
x = 105
So the total money spent by 9 persons = 480+x
= 480+105
= 585
— End of Linear Equations and Inequalities in One Variable Exe-12.2 Class 8 ICSE Maths Solutions :–
Return to : – ML Aggarwal Maths Solutions for ICSE Class -8
Thanks


