ML Aggarwal Logarithms Chapter Test Class 9 ICSE Maths Solutions

ML Aggarwal Logarithms Chapter Test Class 9 ICSE Maths APC Understanding Solutions. Solutions of  Chapter Test. This post is the Solutions of  ML Aggarwal  Chapter 9- Logarithms for ICSE Maths Class-9.  APC Understanding ML Aggarwal Solutions (APC) Avichal Publication Solutions of Chapter-9 Logarithms for ICSE Board Class-9. Visit official website CISCE for detail information about ICSE Board Class-9.

ML Aggarwal Logarithms Chapter Test Class 9 ICSE Maths Solutions

Chapter Test Solutions of ML Aggarwal for ICSE Class-9 Ch-9, Logarithms

Note:- Before viewing Solutions of Chapter -9 Logarithms  Class-9 of ML Aggarwal Solutions .  Read the Chapter Carefully. Then solve all example given in Exercise-9.1, Exercise-9.2, MCQs, Chapter Test.

Logarithms Chapter Test

ML Aggarwal Class 9 ICSE Maths Solutions

Page 179

Question 1. loga …..

Answer: 

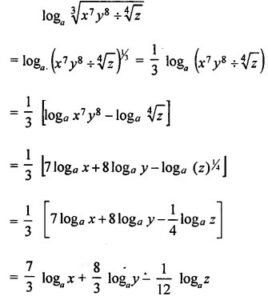
Question 2. Find the value of log√3 3√3 – log5 (0.04)

Answer: 

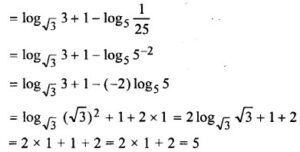
Question 3. Prove the following

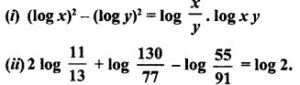
Answer: 

= 2[log 11 – log 13] + [log 130 – log 77] – [log 55 – log 91]

= 2 [log – log 13] + [log 13 × 10 – log 11 × 7] – [log 11 – log 13 × 7]

= 2 [log 11 – log 13] + [(log 13 + log 10) – (log 11 + log 7)] – [(log 11 + log 5) – (log 13 + log 7)]

= 2 log 11 – 2 log 13 + log 10 – log 11 – log 7 – log 11 – log 5 + log 13 + log 7

= (2 log 11 – log 11 – log 11) + (-2 log 13 + log 13 + log 13) + log 10 – log 5 + (log 7 – log 7)

= 0 + 0 + log 10 – log 5 + 0 = log 10 – log 5

= log(10/5)

log 2 = R.H.S

Hence, Result is proved.

Question 4. If log (m + n) = log m + log n, show that n = m/(m-1)

Answer: 

Given log (m + n) = log m + log n
⇒ log (m + n) = log mn ⇒ m + n = mn
⇒ m = mn – n ⇒ m = n (m -1)
⇒ n (m – 1) = m ⇒ n = m/(m-1)
Hence, result is proved.

Question 5. If log (x+y)/2 = 1/2 (log x + log y) prove that x = y.

Answer: 

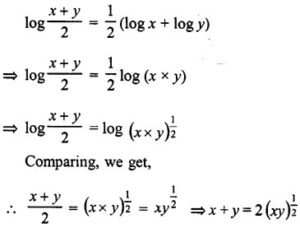
Squaring
⇒ (x + y)² = 4xy ⇒ x² + y² + 2xy = 4xy
⇒ x² + y² + 2xy – 4xy = 0 ⇒ x² + y² – 2xy = 0
⇒ (x – y)² = 0 ⇒ x – y = 0
∴ x = y Hence proved.

Question 6. If a, b are positive real numbers, a > b and a² + b² = 27 ab, prove that

Answer: 

a² + b² = 27ab
⇒ a² + b² – 2ab = 25ab

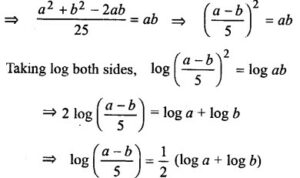
Question 7. Solve the following equations for x:

(i) logx 1/49 = -2

(ii) logx 1/4√2 = -5

(iii) logx 1/243 = 10

(iv) logx 32 = x-4

(v) log7 (2x² – 7)  = 2

(vi) log (x² – 21)  = 2

(vii) log6 (x – 2)(x + 3)  = 1

(viii) log6 (x – 2) + log6 (x + 3)  = 1

(ix) log (x + 1) + log (x – 1) = log 11 + 2 log 3

Answer: 

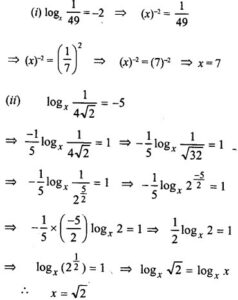
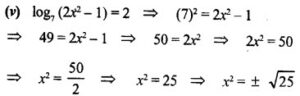
⇒ x = +5, -5

(vi) log (x² – 21) = 2

(10)² = x² – 21 ⇒ 100 = x² – 21
⇒ x² – 21 = 100 ⇒ x² = 100 + 21
⇒ x² = 121 ⇒ x = ±√121 ⇒ x = ±11
∴ x = 11, -11

(vii) log₆ (x – 2) (x + 3) = 1 {∵ log_a a= 1}

Comparing,
(x – 2)(x + 3) = 6
⇒ x² + 3x – 2x – 6 = 6
⇒ x² + x – 6 – 6 = 0
⇒ x² + x- 12 = 0
⇒ x² + 4x – 3x- 12 = 0
⇒ x (x + 4) – 3 (x + 4) = 0
⇒ (x + 4)(x – 3) = 0
Either x + 4 = 0, then x = -4
or x – 3 = 0, then x = 3
Hence x = 3, -4

(viii) log₆ (x – 2) + log₆ (x + 3) = 1

log₆ (x – 2) (x + 3) = 1 = log₆ 6 {∵ log_a a = 1}
Comparing,
(x – 2) (x + 3) = 6 => x² + 3x – 2x – 6 = 6
⇒ x² + x – 6 – 6 = 0 ⇒ x² + x – 12 = 0
⇒ x² + 4x – 3x – 12 = 0
⇒ x (x + 4) – 3 (x + 4) = 0
⇒ (x + 4)(x – 3) = 0
Either x + 4 = 0, then x = -4
or x – 3 = 0, then x = 3
∴ x = 3, -4

(ix) log (x +1) + log (x -1) = log 11 + 2 log 3

⇒ log [(x + 1) (x – 1)] = log 11 + log (3)²
⇒ log (x² – 1) = log 11 + log 9 [∵ a² – b² = (a + b)(a – b)]
⇒ log(x² – 1) = log(11 × 9) ⇒ x² – 1 = 11 × 9
⇒ x² – 1 = 99 × x² = 99 + 1 ⇒ x² = 100
⇒ x² = (10)2² ⇒ x = 10

Question 8. Solve for x and y:

Question 9. If a = 1 + log_xyz, b = 1 + log_y zx and c = 1 + log_zxy, then show that ab + bc + ca = abc.

Answer:

a = 1 + log_xyz
b = 1 + log_yzx
c = 1 + log_zxy
a = 1 + log_xyz = log_xx + log_xyz

—  : End of ML Aggarwal Logarithms Chapter Test Class 9 ICSE Maths Solutions :–

Return to :-  ML Aggarawal Maths Solutions for ICSE  Class-9

Thanks

Please Share with Your Friends