ML Aggarwal Matrices Exe-8.3 Class 10 ICSE Maths Solutions. We Provide Step by Step Answer of Exe-8.3 Questions as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-10.
ML Aggarwal Matrices Exe-8.3 Class 10 ICSE Maths Solutions Ch-8
| Board | ICSE |
| Subject | Maths |
| Class | 10th |
| Chapter-8 | Matrices |
| Writer / Book | Understanding |
| Topics | Solutions of Exe-8.3 |
| Academic Session | 2024-2025 |
Matrices
( ML Aggarwal Matrices Exe-8.3 Class 10 ICSE Maths Solutions )
Question- 1
If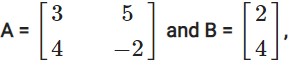 
, is the product AB possible ? Give a reason. If yes, find AB. (2011)
Answer- 1
Yes, the product is possible because of
number of column in A = number of row in B
i.e., (2 x 2). (2 x 1) = (2 x 1) is the order of the matrix.
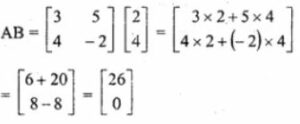
Question- 2
If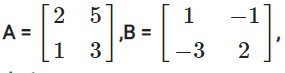 
, find AB and BA, Is AB = BA ?
Answer -2
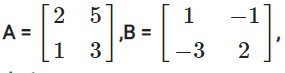
First finding AB
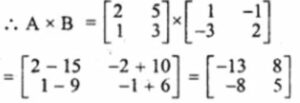
Now Finding BA
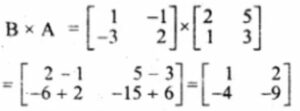
Therefore AB is not equal to BA
Matrices Exe-8.3 Questions
ML Aggarwal Class 10 ICSE Maths Solutions
Page-157
Answer- 1
Yes, the product is possible because of
number of column in A = number of row in B
i.e., (2 x 2). (2 x 1) = (2 x 1) is the order of the matrix.
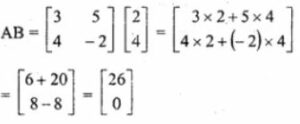
Answer -2
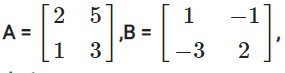
First finding AB
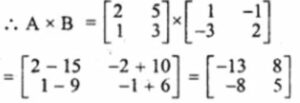
Now Finding BA
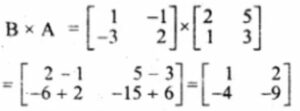
Therefore AB is not equal to BA
Answer-3
AB=
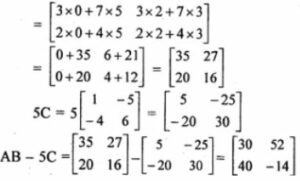
Answer -4
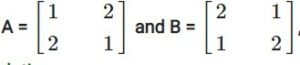
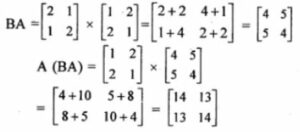
Answer -5
Answer -6
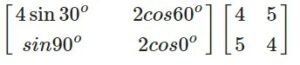
sin 30= 1/2 and cos 60 = 1/2
sin 90=1 cos 0 =1
Answer-7,
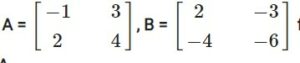
AB=
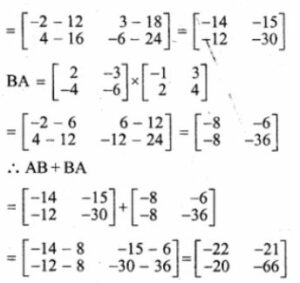
Answer -8
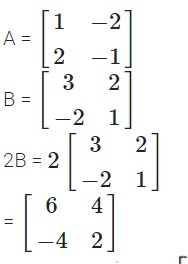
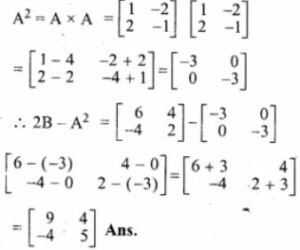
Answer-9
(i) A(B + C)
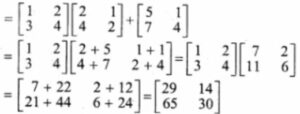
(ii) (B + C)A
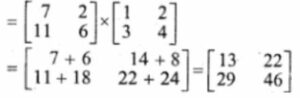
Answer-10
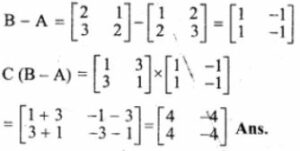
Answer-11
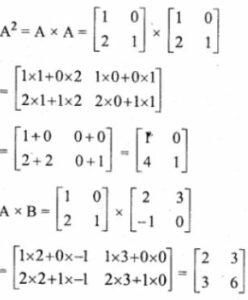
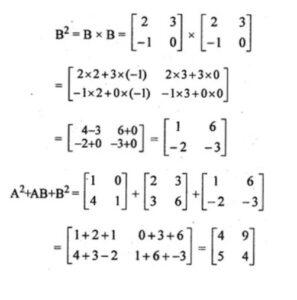
Answer -12
Answer-13
AC+ B² -10 C
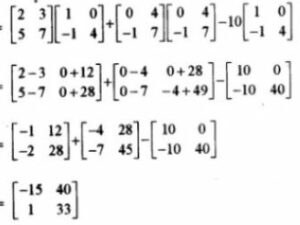
Answer-14
Answer-15
Answer -16
Given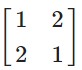
X² – 2X – 3I = 0
Solution =
or
X =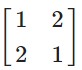
∴ X² =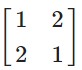
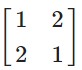
Answer-17
Given
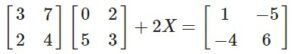
Answer-18
Given
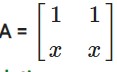
A² =
comparing 1+x =0
x = -1
Answer-19
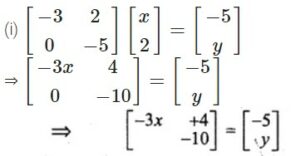
Comparing the corresponding elements,
– 3x + 4 = -5
-3x = -5 – 4 = -9
x = -9/-3 = 3
Therefore, x = 3 and y = -10.
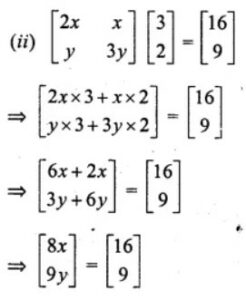
Comparing, we get
8x = 16
⇒ x = 16/8 = 2
And, 9y = 9
y = 9/9 = 1
Answer-20
Given
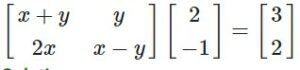
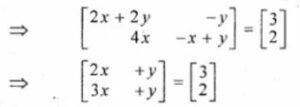
On comparing the corresponding elements,
2x + y = 3 … (i)
3x + y = 2 … (ii)
Subtracting,
-x = 1 ⇒ x = -1
Substituting the value of x in (i),
2(-1) + y = 3
-2 + y = 3
y = 3 + 2 = 5
Therefore, x = -1 and y = 5.
Answer -21
Given
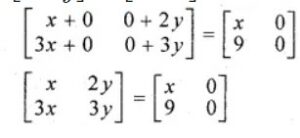
Comparing the corresponding elements
2y = 0
⇒ y = 0
3x = 9
⇒ x = 3
Hence x = 3, y = 0.
Answer -22
Given
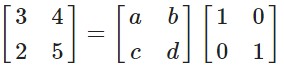
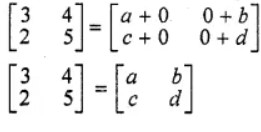
Comparing the corresponding elements
a = 3, b = 4, c = 2, d = 5
Answer -23
A =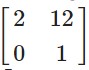 
and
B =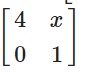 
A² = B
A x A = B
on comparing x=36
Answer-24
Given
A² =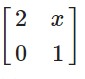 
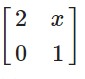
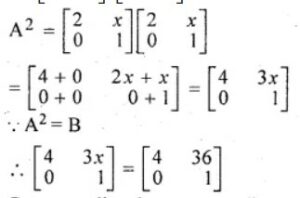
Corresponding the corresponding elements
3x = 36
⇒ x = 12
Hence x = 12.
Answer-25
Given
A =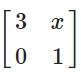 
and B = 
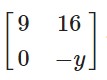find x and y when A² = B
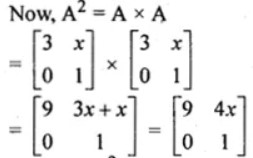
We have A2 = B
Two matrices are equal if each and every corresponding element is equal
⇒ 4x = 16 and 1 = –y
⇒ x = 4 and y = –1.
Answer -26
given
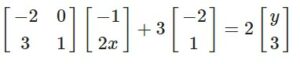
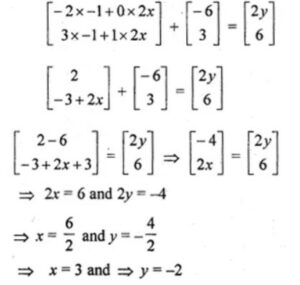
Answer-27
⇒ 
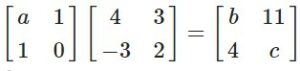
Answer -28
Given
A² =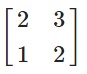 
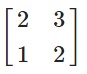
Answer -29
given
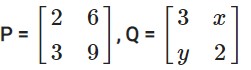
Answer-30
Given
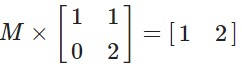
(i) M is the order of 1 x 2
let M = [x y]
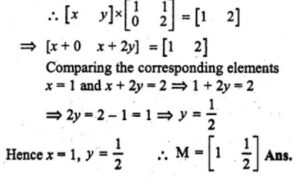
Answer -31
We have
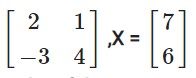
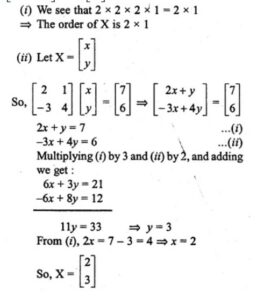
Answer-32
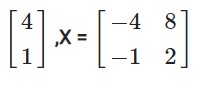
Let matrix X = [x y]
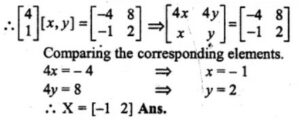
Answer -33
(i) given
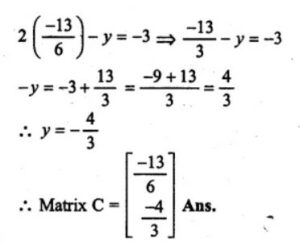
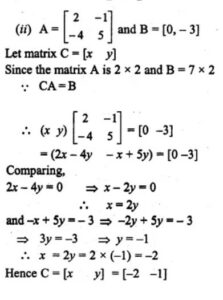
Answer-34
A =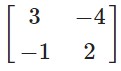 
BA = I, where I is unity matrix of order 2
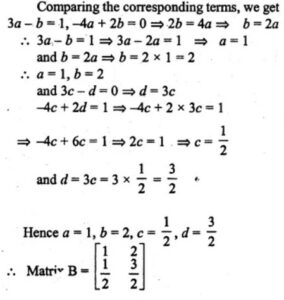
Answer-35
(i)
(ii)
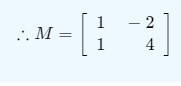
Answer-36
and AB = C
— : End of ML Aggarwal Matrices Exe-8.3 for Class 10 ICSE Maths Solutions :–
Return to :- ML Aggarwal Solutions for ICSE Class-10
Thanks
Please Share with Your Friends
