ML Aggarwal Mensuration Exe-14.2 Class 6 ICSE Maths Solutions. We Provide Step by Step Answer of Exe-14.2 Questions for Mensuration as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-6.
ML Aggarwal Mensuration Exe-14.2 Class 6 ICSE Maths Solutions
| Board | ICSE |
| Publications | Avichal Publishig Company (APC) |
| Subject | Maths |
| Class | 6th |
| Chapter-14 | Mensuration |
| Writer | ML Aggarwal |
| Book Name | Understanding |
| Topics | Solution of Exe-14.2 Questions |
| Edition | 2023-2024 |
Mensuration Exe-14.2
ML Aggarwal Class 6 ICSE Maths Solutions
Page-294
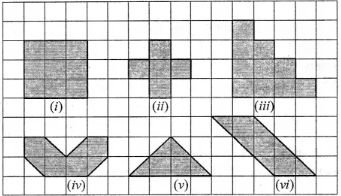
Question 1. Find the area of the region enclosed by the following figures by counting squares:
Answer:

(iii) Fill-filled squares = 10
∴ Total area = Area covered by full squares
= 10 × 1 sq. unit = 10 sq. units
(iv) Full-filled squares = 4
Half-filled squares = 4
Area covered by full squares = 4 × 1 sq. unit = 4 sq. units
Area covered by half squares = 4 × sq. units = 2 sq. units
∴ Total area = 4 sq. units + 2 sq. units = 6 sq. units
(v) Full-fulled squares = 2 Half-filled squares = 4
Area covered by full squarees = 2 × 1 sq. unit = 2 sq. units
Area covered by half squares = 4 × sq. unit = 2 sq. units
∴ Total area = 2 sq. units + 2 sq. units = 4 sq. units.
(vi) Full-filled squares = 3
Half-filled squares = 6
Area covered by full squares = 3 × 1 sq. unit = 3 sq. units
Area covered by half squares = 6 × sq. unit = 3 sq. units
∴ Total area = 3 sq. units + 3 sq. units = 6 sq. units
Question 2. Find the areas of the rectangles whose lengths and breadths are:
(i) 9 m and 6 m
(ii) 17 m and 3 m
(iii) 14 m and 4 m
Which one has the largest area and which one has the smallest area?
Answer:
(i) Area of the rectangle = Length × Breadth = 9 m × 6 m = 54 sq. m
(ii) Area of the rectangle = Length × Breadth = 17 m × 3 m = 51 sq. m
(iii) Area of the rectangle = Length × Breadth = 14 m × 4 m = 56 sq. m
The rectangle (iii) has the largest area and rectangle (ii) smallest area.
Question 3. Find the areas of the rectangles whose two adjacent sides are:
(i) 14 cm and 23 cm
(ii) 3 km and 4 km
(iii) 2 m and 90 cm
Answer:
(i) 14 cm and 23 cm
Area of the rectangle = Length × Breadth
= 14 cm × 23 cm
= 322 sq. cm
(ii) 3 km and 4 km
Area of the rectangle = Length × Breadth
= 3 km × 4 km
= 12 sq. km
(iii) 2 m and 90 cm
90 cm = 0.9 m
Area of the rectangle = l × b
= 2 m × 0.9 m
= 1.8 sq. m
Question 4. Find the areas of the squares whose sides are:
(i) 8 cm
(ii) 14 m
(iii) 2 m 50 cm
Answer:
(i) 8 cm
Area of the square = Side × Side = 8 cm × 8 cm = 64 sq. cm
(ii) 14 m
Area of the square = Side × Side = 14 m × 14 m = 196 sq. m
(iii) 2 m 50 cm
50 cm = 50/100 = 0.5 m
∴ Side = 2.5 m
Area of the square = Side × Side = 2.5 m × 2.5 m = 6.25 sq. m
Mensuration Exe-14.2
ML Aggarwal Class 6 ICSE Maths Solutions
Page-295
Question 5. A room is 4 m long and 3 m 25 cm wide. How many square metres of carpet is needed to cover the floor of the room?
Answer:
Length of the room = 4 m
Breadth of the room = 3 m 25 cm = 3.25 m
∴ Area of the room = Length × Breadth = 4 × 3.25 sq. m = 13 sq. m
Hence, 13 square metres of carpet is needed to cover the floor of the room.
Question 6. What is the cost of tiling a rectangular field 500 m long and 200 m wide at the rate of ₹7.5 per hundred square metres?
Answer:
Length of the rectangular field = 500 m
Breadth of the rectangular field = 200 m
∴ Area of the rectangular field = Length × Breadth
= 500 m × 200 m = 10000 sq. m
∵ Cost of tiling 100 sq. m = ₹7.5
∴ Cost of tiling 1 sq. m = ₹7.5/100
∴ Cost of tiling 100000 sq. m = ₹ (7.5/100) x 100000 = ₹7500
Question 7. A floor is 5 m long and 4 m wide. A square carpet of sides 3 m is laid on the floor. Find the area of the floor that is not carpeted.
Answer:
Length of the floor = 5 m
Breadth of the floor = 4 m
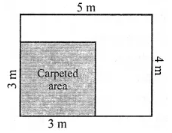
∴Area of the floor = Length × Breadth = 5 m × 4 m = 20 sq m
Area of the square carpet = Side × Side = 3 m × 3 m = 9 sq m
∴ Area of the floor that is not carpeted = 20 sq m – 9 sq m = 11 sqm
Question 8. In the given figure, find the area of the path (shown shaded) which is 2 m wide all around.

Answer:
Length of field = 100 m
Breadth of field = 60 m
Area of the field = L × B = 100 × 60 = 6000m2
Length of field exclude path = 100 – (2 + 2) = 96 m
Breadth of field exclude path = 60 – (2 + 2) = 56
Area of field exclude path = L × B = 96 m × 56 m = 5376 m2
Area of path = Area of field – Area of field exclude path = 6000 – 5376 = 624 sq. m
Question 9. Four square flower beds of side 1 m 50 cm are dug on a rectangular piece of land 8 m long and 6 m 50 cm wide. What is the area of the remaining part of the land?
Answer:
Area of 1 square flower bed = a2 = 1.5 × 1.5 = 2.25 m2
Area of 4 square flower bed = 4 × 2.25 = 9 m2
Length of land = 8m
Breadth of land = 6.5 m
Area of land = l × b = 8 × 6.5 = 52 m2
Area of remaining part of bed = 52 – 9 = 43 sq. m
Question 11. How many tiles whose length and breadth are 12 cm and 5 cm respectively will be needed to cover a rectangular region whose length and breadth are respectively :
(i) 70 cm and 36 cm
(ii) 144 cm and 1 m.
Answer:
(i) Length (l) of tile = 12 cm
breadth (b) of tile = 5 cm
Area of tile = 1 × b = 12 cm × 5 cm = 60 cm2
Length (l) of rectangular region = 70 cm
breadth (b) of rectangular region = 36 cm
Area of rectangular region = l × b = 70 cm × 36 cm = 2520 cm2
If 60 cm2 area is covered then tile required = 1
If 2520 cm2 area is covered then tile required is = (1/60) x 25202 cm = 42
Hence, 42 tiles are required.
(ii) Area of the tile = 60 cm2 (as in (i) above)
Length (l) of rectangular region = 1 m = 100 cm
breadth (b) of rectangular region = 144 cm
Area of rectangular region = 100 cm × 144 cm = 14400 cm2
If 60 cm2 are is covered then tile required = 1
If 14400 cm2 is covered then tile required = (1/60) x 14400 cm2 = 240
Hence, 240 tiles are required.
Question 11. The area of a rectangular plot is 340 sq. m. If its breadth is 17 m, find its length and the perimeter.
Answer:
Area of plot A = 340m2
Length (l) = ?
Area = l × b
⇒ 340 = l × 17
⇒ 340/17
⇒ l = 20
Length = 20 m
Perimeter = 2 (l + b) = 2 (20 + 17) = 2 (37) = 74 m
Question 12. If the area of a rectangular plot is 144 sq. m and its length is 16 m. Find the breadth of the plot and the cost of fencing it at the rate of ?6 per metre.
Answer:
Area of plot = 144 m2
Length (l) = 16 m.
Breadth (b) = ?
Area = l × b
⇒ 144 = 16 × b
⇒ 144/16 = b
⇒ b = 9 m
Cost of fencing is ₹6 per metre
Perimeter of field = 2(l + b) = 2 (16 + 9) = 50 m
Cost of fencing = 50 × 6 = ₹300
Question 13. The perimeter of a square is equal to that of a rectangle of length 17 m and breadth 11 m. Find the area of the square.
Answer:
Length = 17 m
Breadth = 11 m
Perimeter of rectangle = 2(l+b) = 2(17+11)
= 56 m
Perimeter of rectangle = Perimeter of square
= 56 m
Perimeter of square = 56 m
4 × side = 56
Side = 56/4 = 14m
Area of square = side × side = 14 × 14
= 196m sq.
Question 14. A rectangle has same area as that of a square of side 10m. If the breadth of the rectangle is 8 m, find the perimeter of the rectangle.
Answer:
Area of square
= Side × Side
= 10 × 10
= 100m²
According to given conditions;
Area of rectangle = Area of square
length × breadth = 100m²
length × 8 = 100m²
length = 100 ÷ 8
length = 12.5 m
Perimeter of rectangle
= 2 (length + breadth)
= 2 (12.5 + 8)
= 2 × 20.5
= 41m
Question 15. Split the following shapes into rectangles and find their areas. (The measures are given in centimetres).

Answer:
(a) The given figure is split into 2 rectangles.

Length of Part I = 12 cm
Breadth of Part I = 2 cm
Area of Part I = Length × Breadth = (12 × 2) cm2 = 24 cm2
Length of Part II = 8 cm
Breadth of Part II = 2 cm
Area of Part II = l × b = (8 × 2) cm2 = 16 cm2
∴ Total area = Area of Part I + Area of Part II = (24 + 16) cm2 = 40 cm2
(b) The given figure is divided into 5 parts

Here length of all the rectangles = 7 cm
and breadth of all the rectangles = 7 cm
Area = l × b = 7 × 7 = 49 cm2
Total rectangles = 5
∴ Total area = 5 × 49 cm2 = 245 cm2
(c) The given figure is divided into 2 rectangles

Length of Ist Part = 4 cm
Breadth of IInd Part = 1 cm
Area = l × b = 4 × 1 = 4 cm2
Length of IInd Part = 5 cm
Breadth of IInd Part = 1 cm
Area = l × b = 5 × 1 = 5 cm2
∴ Total area = 4 cm2 + 5 cm2 = 9 cm2
— : End of ML Aggarwal Mensuration Exe-14.2 Class 6 ICSE Maths Solutions :–
Return to – ML Aggarwal Maths Solutions for ICSE Class -6
Thanks



Very good .com