ML Aggarwal Playing With Numbers Exe-4.5 Class 6 ICSE Maths Solutions. We Provide Step by Step Answer of Exe-4.5 Questions for Playing With Numbers as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-6.
ML Aggarwal Playing With Numbers Exe-4.5 Class 6 ICSE Maths Solutions
| Board | ICSE |
| Publications | Avichal Publishig Company (APC) |
| Subject | Maths |
| Class | 6th |
| Chapter-4 | Playing With Numbers |
| Writer | ML Aggarwal |
| Book Name | Understanding |
| Topics | Solution of Exe-4.5 Questions |
| Edition | 2023-2024 |
Playing With Numbers Exe-4.5
ML Aggarwal Class 6 ICSE Maths Solutions
Page-86
Question 1. Find the L.C.M. of the given numbers by prime factorization method :
(i) 28, 98
(ii) 36, 40, 126
(iii) 108, 135, 162
(iv) 24, 28, 196.
Answer:
(i) Prime factorization of the given number are
28 = 2 x 2 x 7
98 = 2 x 7 x 7
Here 2 and 7 occurs as a prime factor maximum 2 times
so, LCM = 2x 2 x 7 x 7 = 196
(ii) Prime factorization of the given number are
36 = 2 x 2 x 3 x 3
40 = 2 x 2 x 2 x 5
126 = 2 x 3 x 3 x 7
2 occurs as a prime factor maximum 3 times,
3 two times , 5 and 7 are one time
so, LCM = 2x 2 x 2 x 3 x 3 x 5 x 7 = 2520
(iii) Prime factorization of the given number are
108 = 2 x 2 x 3 x 3 x 3
135 = 3 x 3 x 3 x 5
162 = 2 x 3 x 3 x 3 x 3
2 occurs as a prime factor maximum 2 times,
3 four times , 5 one time
so, LCM = 2x 2 x 3 x 3 x 3 x 3 x 5 = 1720
(iv) Prime factorization of the given number are
24 = 2 x 2 x 2 x 3
28 = 2 x 2 x 7
196 = 2 x 7 x 7 x 7
2 occurs as a prime factor maximum 3 times,
3 one times , 7 two times
so, LCM = 2x 2 x 2 x 3 x 7 x 7 = 1176
Playing With Numbers Exe-4.5
ML Aggarwal Class 6 ICSE Maths Solutions
Page-87
Question 2. Find the L.C.M. of the given numbers by division method :
(i) 480, 672
(ii) 6, 8, 45
(iii) 24, 40, 84
(iv) 20, 36, 63, 67
Answer:
(i) 480, 672

So, LCM = 2 x 2 x 2 x 2 x 2 x 3 x 5 x 7 = 3360
(ii) 6, 8, 45

So, LCM = 2 x 2 x 2 x 3 x 3 x 5 = 360
(iii) 24, 40, 84

So, LCM = 2 x 2 x 2 x 3 x 5 x 7 = 840
(iv) 20, 36, 63, 67
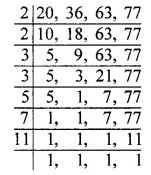
So, LCM = 2 x 2 x 2 x 3 x 3 x 5 x 7 x 11 = 813860
Question 3 . Find the least number which when increased by 15 is exactly divisible by 15, 35 and 48.
Answer:
First, we find the least number which is exactly divisible by the numbers 15, 35 and
48. For this, we find L.C.M. of 15, 35 and 48

L.C.M. = 3 x 5 x 7 x 2 x 2 x 2 x 2 = 1680
According to given condition, the required number will be 15 less than 1680.
The required least number 1680 -15 = 1665
Question 4. Find the least number which when divided by 6, 15 and 18 leaves remainder 5 in each case.
Answer:
L.C.M. of 6, 15 and 18
= 2 x 3 x 3 x 5 = 90
Hence, the required number is 90 + 5 … (ex. 95)
Question 5. Find the least number which when divided by 24, 36, 45 and 54 leaves a remainder of 3 in each case.
Answer:
24, 36, 45 and 54
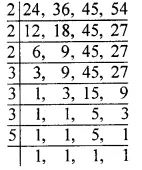
So, LCM = 2 x 2 x 2 x 3 x 3 x 3 x 5 = 1080
According to given condition the number will be 3 more than 1080.
So, The required number = 1080 + 3 = 1083
Question-6. Find the greatest 3-digit number which is exactly divisible by 8, 20 and 24.
Answer:
We, find the LCM of 8, 20 and 24

LCM of given numbers = 2 x 2 x 2 x 3 x 5 = 120
Greatest number of 3 digit is 999
We divide 999 by 120 and find the remainder.

According to given condition, we need a greatest 3-digit number which is exactly
divisible by 120.
So, The required number = 999 – 39 = 960
Question 7. Find the smallest 4-digit number which is exactly divisible by 32, 36 and 48.
Answer:
We, find the LCM of 32, 36 and 48

LCM of given numbers = 2 x 2 x 2 x 2 x 2 x 3 x 3 = 288
Smallest number of 4 digit is 1000
We divide 1000 by 288 and find the remainder.

According to given condition, we need a least number which is exactly
divisible by 288.
So, The required number = 1000 + (288- 136) = 1152
Question 8. Find the greatest 4-digit number which is exactly divisible by each of 8, 12 and 20.
Answer:
We, find the LCM of 8, 12 and 20

LCM of given numbers = 2 x 2 x 3 x 5 = 120
According to given condition, we need a greatest number which is exactly
divisible by 120
Greatest number of 4 digit = 9999
We divide 9999 by 120 and find the remainder.
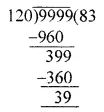
So, The required number = 9999 – 39 = 9960
Question 9. Find the least number of five digits which is exactly divisible by 32, 36 and 45.
Answer:
We, find the LCM of 32, 36 and 45

LCM of given numbers = 2 x 2 x 2 x 2 x 3 x 3 x 5 = 1440
Smallest number of 5 digit = 10000
We divide 10000 by 1440 and find the remainder.

According to given condition, we need a least number which is exactly
divisible by 1440.
So, The required number = 10000 + 1440 – 1360
= 10080
Question 10. Three boys step off together from the same spot. Their steps measure 63 cm, 70 cm and 77 cm respectively. What is the minimum distance each should cover so that all can cover the same distance in complete steps?
Answer:
LCM of 63, 70 and 77
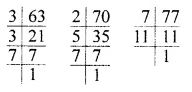
63 = 3 x 3 x 7
70 = 2 x 5 x 7
77 = 7 x 11
so, LCM = 3 x 3 x 2 x 5 x 7 x 11 = 6930
so The minimum distance each will cover is 6930 cm
ex. 69 m 30 cm
Question 11. Traffic lights at three different road crossing change after 48 seconds, 72 seconds and 108 seconds respectively. At what time will they change together again if they change simultaneously at 7 A.M.?
Answer:
LCM of 48, 72 and 108

2 x 2 x 2 x 2 x 3 x 3 x 3 = 432
432 second = 7 minute 12 second past 7 AM
Question 12. If the product of two numbers is 4032 and their HCF is 12, find their LCM.
Answer
The product of two numbers is 4032
HCF = 12
LCM = 4032 / 12
336
Question 13. The HCF and LCM of two numbers are 9 and 270 respectively. If one of the numbers is 45, find the other number.
Answer:
HCF x LCM = one number x other number
9 x 270 = 45 x 2nd number
2430 = 45 x 2nd number
2430/45 = 162/3 54
So, 54 is the other number
Question 14. Find the HCF of 180 and 336. Hence, find their LCM.
Answer:
Division method : HCF of 180 and 336

So, HCF of 180 and 336 = 12
Products of number LCM of 180 and 336 = Products of number/ their HCF
= (180 x 336)/ 12
=15 x 336
= 5040
Question 15. Can two numbers have 15 as their HCF and 110 as their LCM? Give reason to justify your answer.
Answer:
One dividing 110 by 15, we get
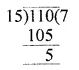
7 is quotient and 5 is reminder
We find that the reminder ≠ 0
So, 110 is not exactly divisible by 15
So, HCF and LCM of two number can not be 15 and 115 respectively.
As LCM of two number is always exactly divisible by their HCF.
— : End of ML Aggarwal Playing With Numbers Exe-4.5 Class 6 ICSE Maths Solutions :–
Return to – ML Aggarwal Maths Solutions for ICSE Class -6
Thanks


