ML Aggarwal Quadratic Equations Exe-5.2 Class 10 ICSE Maths Solutions

ML Aggarwal Quadratic Equations Exe-5.2 Class 10 ICSE Maths Solutions . We Provide Step by Step Answer of Exe-5.2 Questions for Quadratic Equations in One Variable as council prescribe guideline for upcoming board exam.  Visit official Website CISCE  for detail information about ICSE Board Class-10.

ML Aggarwal Ch-5 Quadratic Equations in one Variable Exercise- 5.2 Class 10 ICSE Maths Solutions

Board	ICSE
Subject	Maths
Class	9th
Chapter-5	Quadratic Equations
Writer / Book	Understanding
Topics	Solutions of Exe-5.2
Academic Session	2024-2025

 Quadratic Equations in one Variable Exe-5.2

(Class 10 ICSE ML Aggarwal Maths Solutions)

Solve the following equations (1 to 18) by factorization

Question-1

(i) x² – 3x – 10 = 0
(ii) x(2x + 5) = 3

Answer -1

(i) x² – 3x – 10 = 0
⇒ x² – 5x + 2x – 10 = 0
⇒ x(x – 5) + 2(x – 5) = 0

(x + 2) (x – 5) =0

So now,

(x + 2) = 0 or (x – 5) =0

x = -2 or x = 5

∴ Value of x = -2, 5

(ii) x(2x + 5) = 3

Let us simplify the given expression,

2x² + 5x – 3 = 0

Now, let us factorize

2x² + 6x – x – 3 = 0

2x(x + 3) -1(x + 3) = 0

(2x – 1) (x + 3) = 0

So now,

(2x – 1) = 0 or (x + 3) = 0

2x = 1 or x = -3

x = ½ or x = -3

∴ Value of x = ½, -3

Question-2

(i) 3x² – 5x – 12 = 0
(ii) 21x² – 8x – 4 = 0

Answer -2

(i) 3x² – 5x – 12 = 0
⇒ 3x² – 9x + 4x – 12 = 0
⇒ 3x (x – 3) + 4(x – 3) = 0

(3x + 4) (x – 3) =0

So now,

(3x + 4) = 0 or (x – 3) =0

3x = -4 or x = 3

x = -4/3 or x = 3

∴ Value of x = -4/3, 3

(ii) 21x² – 8x – 4 = 0

Let us simplify the given expression,

21x² – 14x + 6x – 4 = 0

7x(3x – 2) + 2(3x – 2) = 0

(7x + 2) (3x – 2) = 0

So now,

(7x + 2) = 0 or (3x – 2) = 0

7x = -2 or 3x = 2

x = -2/7 or x = 2/3

∴ Value of x = -2/7, 2/3

Question -3

(i) 3x² = x + 4
(ii) x (6x – 1) = 35

Answer-3

(i) 3x² = x + 4
⇒ 3x² – x – 4 = 0
⇒ 3x² – 4x + 3x – 4 = 0

x(3x – 4) + 1(3x – 4) = 0

(x + 1) (3x – 4) = 0

So now,

(x + 1) = 0 or (3x – 4) = 0

x = -1 or 3x = 4

x = -1 or x = 4/3

∴ Value of x = -1, 4/3

(ii) x(6x – 1) = 35

Let us simplify the given expression,

6x² – x – 35 = 0

Now, let us factorize

6x² – 15x + 14x – 35 = 0

3x(2x – 5) + 7(2x – 5) = 0

(3x + 7) (2x – 5) = 0

So now,

(3x + 7) = 0 or (2x – 5) = 0

3x = -7 or 2x = 5

x = -7/3 or x = 5/2

∴ Value of x = -7/3, 5/2

Question -4

(i) 6p² + 11p – 10 = 0

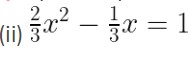
Answer -4

(i) 6p² + 11p – 10 = 0
⇒ 6p² + 15p – 4p – 10 = 0
⇒ 3p(2p + 5) – 2(2p + 5) = 0

(3p – 2) (2p + 5) = 0

So now, (3p – 2) = 0 or (2p + 5) = 0

3p = 2 or 2p = -5

p = 2/3 or p = -5/2

∴ Value of p = 2/3, -5/2

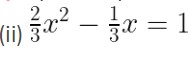
Let us simplify the given expression,

2x² – x = 3

2x² – x – 3 = 0

Let us factorize the given expression,

2x² – 3x + 2x – 3 = 0

x(2x – 3) + 1(2x – 3) = 0

(x + 1) (2x – 3) = 0

(x + 1) = 0 or (2x – 3) = 0

x = -1 or 2x = 3

x = -1 or x = 3/2

∴ Value of x = -1, 3/2

Question -5

(i) 3(x – 2)² = 147

(ii) ¹⁄₇.(3x – 5)² = 28.

Answer-5

(i) 3(x – 2)² = 147

on expanding

3(x² – 4x + 4) = 147

3x² – 12x + 12 = 147

3x² – 12x +12 – 147 = 0

3x² – 12x – 135 = 0

Divide by 3, we get

x² – 4x – 45 = 0

Let us factorize the expression,

x² – 9x + 5x – 45 = 0

x(x – 9) + 5(x – 9) = 0

(x + 5) (x – 9) = 0

So now,

(x + 5) = 0 or (x – 9) = 0

x = -5 or x = 9

∴ Value of x = -5, 9

(ii) 1/7(3x – 5)² = 28

Let us simplify the expression,

(3x – 5)² = 28 × 7

(3x – 5)² = 196

Now let us expand,

9x² – 30x + 25 = 196

9x² – 30x + 25 – 196 = 0

9x² – 30x – 171 = 0

Divide by 3, we get

3x² – 10x – 57 = 0

Let us factorize the expression,

3x² – 19x + 9x – 57 = 0

x(3x – 19) + 3(3x – 19) = 0

(x + 3) (3x – 19) = 0

So now,

(x + 3) = 0 or (3x – 19) = 0

x = -3 or 3x = 19

∴ Value of x = -3, 19/3

---

ML Aggarwal Quadratic Equations in one Variable Exercise- 5.2 Class 10 ICSE Maths Solutions

Question-6

x² – 4x – 12 = 0,when x ∈ N

Answer-6

x² – 4x – 12 = 0
⇒ x² – 6x + 2x – 12 = 0
⇒ x (x – 6) + 2 (x – 6) = 0
⇒ (x – 6) (x + 2) = 0
Either x – 6 = 0, then x = 6
or x + 2 = 0, then x = -2
But -2 is not a natural number
∴ x = 6

Question -7

2x² – 9x + 10 = 0, When
(i) x ∈ N
(ii) x ∈ Q

Answer -7

2x² – 9x + 10 = 0
⇒ 2x² – 4x – 5x + 10 = 0
⇒ 2x(x – 2) – 5(x – 2) = 0

(2x – 5) (x – 2) = 0

So now,

(2x – 5) = 0 or (x – 2) = 0

2x = 5 or x = 2

x = 5/2 or x = 2

(i) When, x ∈ N then, x = 2

(ii) When, x ∈ Q then, x = 2, 5/2

Question -8

(i) a²x² + 2ax + 1 = 0, a≠0
(ii) x² – (p + q)x + pq = 0

Answer -8

(i) a²x² + 2ax + 1 = 0
⇒ a²x² + ax + ax + 1 = 0

ax(ax + 1) + 1(ax + 1) = 0

(ax + 1) (ax + 1) = 0

So now,

(ax + 1) = 0 or (ax + 1) = 0

ax = -1 or ax = -1

x = -1/a or x = -1/a

∴ Value of x = -1/a, -1/a

(ii) x² – (p + q)x + pq = 0

Let us simplify the expression,

x² – (p + q)x + pq = 0

x² – px – qx + pq = 0

x(x – p) – q(x – p) = 0

(x – q) (x – p) = 0

So now,

(x – q) = 0 or (x – p) = 0

x = q or x = p

Question-9

a²x² + (a² + b²)x + b² = 0, a≠0

Answer-9

a²x² + (a² + b²)x + b² = 0
⇒ a²x(x + 1) + b²(x + 1) = 0

(a²x + b²) (x + 1) = 0

So now,

(a²x + b²) = 0 or (x + 1) = 0

a²x = -b² or x = -1

x = -b²/a² or x = -1

∴ Value of x = -b²/a², -1

Question-10

(i) √3x² + 10x + 7√3 = 0
(ii) 4√3x² + 5x – 2√3 = 0

Answer -10

(i) √3x² + 10x + 7√3 = 0
[ ∵ √3 x 7√3 = 7 x 3 = 21] ⇒ √3x(x + √3) + 7(x + √3) = 0

(√3x + 7) (x + √3) = 0

So now,

(√3x + 7) = 0 or (x + √3) = 0

√3x = -7 or x = -√3

x = -7/√3 or x = -√3

∴ Value of x = -7/√3, -√3

(ii) 4√3x² + 5x – 2√3 = 0

on factorize

4√3x² + 8x – 3x – 2√3 = 0 [As, 4√3 × (-2√3) = -8 × 3 = -24 and 8 × (-3) = -24]

4x(√3x + 2) – √3(√3x + 2) = 0

(4x – √3) (√3x + 2) = 0

So now,

(4x – √3) = 0 or (√3x + 2) = 0

4x = √3 or √3x = -2

x = √3/4 or x = -2/√3

---

ML Aggarwal Quadratic Equations in one Variable

(Exercise- 5.2 Class 10 ICSE Maths Solutions)

Question -11

(i) x² – (1 + √2)x + √2 = 0
(ii) x + 1/ x = 41/2

Answer -11

(i) x² – (1 + √2)x + √2 = 0
⇒ x² – x – √2x + √2 = 0

x(x – 1) – √2(x – 1) = 0

(x – 1) (x – √2) = 0

So now,

(x – 1) = 0 or (x + √2) = 0

x = 1 or x = -√2

∴ Value of x = 1, -√2

(ii) x + 1/x = 41/2

(x² + 1)/x = 41/20

20(x² + 1) = 41x

20x² + 20 = 41x

20x² – 41x + 20 = 0

on factorize

20x² – 25x – 16x + 20 = 0

5x(4x – 5) – 4(4x – 5) = 0

(5x – 4) (4x – 5) = 0

So,

(5x – 4) = 0 or (4x – 5) = 0

5x = 4 or 4x = 5

x = 4/5 or x = 5/4

Question -12

Answer -12

(i) 2/x² – 5/x + 2 = 0

Taking L.C.M for the given expression,

(2 – 5x + 2x²)/x² = 0

2x² – 5x + 2 = 0

Now, on factorizing the above expression we get

2x² – 4x – x + 2 = 0

2x(x – 2) – 1(x – 2) = 0

(2x – 1) (x – 2) = 0

So,

(2x – 1) = 0 or (x – 2) = 0

2x = 1 or x = 2

x = ½ or x = 2

∴ Value of x = ½, 2

(ii) x²/15 – x/3 – 10 = 0

Taking L.C.M for the given expression,

(x² – 5x – 150)/15 = 0

x² – 5x – 150 = 0

Now, on factorizing the above expression we get

x² – 15x + 10x – 150 = 0

x(x – 15) + 10(x – 15) = 0

(x – 15) (x + 10) = 0

So,

(x – 15) = 0 or (x + 10) = 0

x = 15 or x = -10

Question-13

(i) 3x – 8/x = 2 (ii) (x + 2)/(x + 3) = (2x – 3)/(3x – 7).

Answer -13

(i) 3x – 8/x = 2

on L.C.M,

(3x² – 8)/x = 2

3x² – 8 = 2x

3x² – 2x – 8 = 0

On factorizing

3x² – 6x + 4x – 8 = 0

3x(x – 2) + 4(x – 2) = 0

(3x + 4) (x – 2) = 0

(3x – 4) = 0 or (x – 2) = 0

3x = 4 or x = 2

x = 4/3 or x = 2

∴ Value of x = 4/3, 2

(ii) (x + 2)/(x + 3) = (2x – 3)/(3x – 7)

(x + 2) (3x – 7) = (2x – 3) (x + 3)

3x² – 7x + 6x – 14 = 2x² + 6x – 3x – 9

3x² – x – 14 = 2x² + 3x – 9

3x² – 2x² – x – 3x – 14 + 9 = 0

x² – 4x – 5 = 0

x² – 5x + x – 5 = 0

x(x – 5) + 1(x – 5) = 0

(x + 1) (x – 5) = 0

x + 1 = 0 or x – 5 = 0

x = -1 or x = 5

Question -14

(i)  8/(x + 3) – 3/(2 – x) = 2
(ii) x/(x – 1) + (x – 1)/x = 2½

Answer -14

(i) 8/(x + 3) – 3/(2 – x) = 2

Taking L.C.M, we have

[8(2 – x) – 3(x + 3)]/[(x + 3)(2 – x)] = 2

16 – 8x – 3x – 9 = 2 (x + 3) (2 – x)

7 – 11x = 2 (2x + 6 – x² – 3x)

7 – 11x = 2 (6 – x² – x)

7 – 11x = 12 – 2x² – 2x

2x² – 11x + 2x + 7 – 12 = 0

2x² – 9x – 5 = 0

2x² – 10x + x – 5 = 0

2x(x – 5) + 1(x – 5) = 0

(2x + 1) (x – 5) = 0

2x + 1 = 0 or x – 5 = 0

x = -1/2 or x = 5

∴ Value of x = -1/2, 5

(ii) x/(x – 1) + (x – 1)/x = 2½

Taking L.C.M, we have

[x² + (x – 1)²] / x(x- 1) = 5/2

(x² + x² – 2x + 1)/ (x² – x) = 5/2

(2x² – 2x + 1)/ (x² – x) = 5/2

2 (2x² – 2x + 1) = 5 (x² – x)

4x² – 4x + 2 = 5x² – 5x

5x² – 4x² – 5x + 4x – 2 = 0

x² – x – 2 = 0

x² – 2x + x – 2 = 0

x(x – 2) + 1(x – 2) = 0

(x + 1) (x – 2) = 0

x + 1 = 0 or x – 2 = 0

x = -1 or x = 2

Question -15

(i)  (x + 1)/(x – 1) + (x – 2)/(x + 2) = 3

(ii)   1/(x – 3) – 1/(x + 5) = 1/6

Answer -15

(i) (x + 1)/(x – 1) + (x – 2)/(x + 2) = 3

[(x + 1) (x + 2) + (x – 2) (x – 1)]/[(x – 1)(x + 2)] = 3

On expanding,

x² + 3x + 2 + x² – 3x + 2 = 3 (x – 1) (x + 2)

2x² + 4 = 3 (x² + x – 2)

2x² + 4 = 3x² + 3x – 6

3x² – 2x² + 3x – 6 – 4 = 0

x² + 3x – 10 = 0

x² + 5x – 2x – 10 = 0

x(x + 5) – 2(x – 5) = 0

(x + 5) (x – 5) = 0

x + 5 = 0 or x – 5 = 0

x = -5 or x = 5

(ii) 1/(x – 3) – 1/(x + 5) = 1/6

[x + 5 – (x – 3)] / [(x – 3) (x + 5)] = 1/6

(x + 5 – x + 3) / [(x – 3) (x + 5)] = 1/6

8/ [(x – 3) (x + 5)] = 1/6

8 × 6 = (x – 3) (x + 5)

48 = x² + 5x – 3x – 15

x² + 2x – 15 – 48 = 0

x² + 2x – 63 = 0

x² + 9x – 7x – 63 = 0

x(x + 9) – 7(x + 9) = 0

(x – 7) (x + 9) = 0

x – 7 = 0 or x + 9 = 0

x = 7 or x = -9

---

Quadratic Equations in one Variable Exercise- 5.2

(ML Aggarwal Class 10 ICSE Maths Solutions)

Question-16

(i) a/(ax – 1) + b/(bx – 1) = a + b, a + b ≠ 0, ab ≠ 0
 

Answer -16

(i) a/(ax – 1) + b/(bx – 1) = a + b, a + b ≠ 0, ab ≠ 0

rearrange the equation

[a/(ax – 1) – b] + [b/(bx – 1) – a] = 0

[a – b(ax – 1)]/(ax – 1) + [b – a(bx – 1)]/(bx – 1) = 0

(a – abx + b)/(ax – 1) + (b – abx + a)/(bx – 1) = 0

(a – abx + b) [1/(ax – 1) + 1/(bx – 1)] = 0

(a – abx + b) [(bx – 1 + ax – 1)/(ax – 1)(bx – 1)] = 0

(a – abx + b) [(ax + bx – 2)/ (ax – 1)(bx – 1)] = 0

(a – abx + b) = 0 or (ax + bx – 2)/ [(ax – 1) (bx – 1)] = 0

If (a – abx + b) = 0,

a + b = abx

x = (a + b)/ab

if (ax + bx – 2)/ [(ax – 1) (bx – 1)] = 0

ax + bx – 2 = 0

(a + b)x = 2

x = 2/(a + b)

∴ Value of x = (a + b)/ab, 2/(a + b)

(ii)

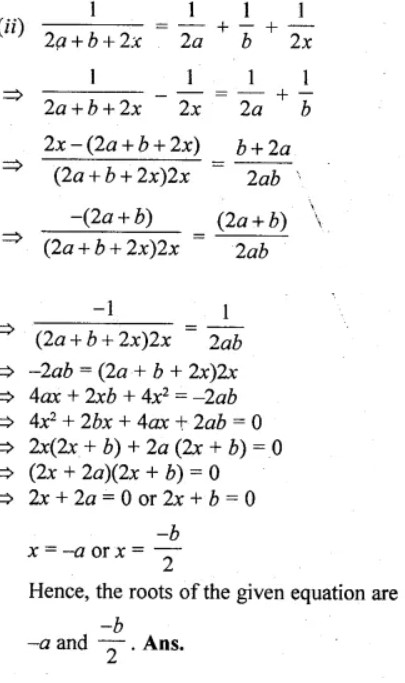
Question -17

1/(x + 6) + 1/(x – 10) = 3/(x – 4)

Answer -17

1/(x + 6) + 1/(x – 10) = 3/(x – 4)

[(x – 10) + (x + 6)]/ [(x + 6) (x – 10)] = 3/(x- 4)

(2x – 4)/ (x² – 4x – 60) = 3/(x- 4)

(2x – 4) (x – 4) = 3(x² – 4x – 60)

2x² – 8x – 4x + 16 = 3x² – 12x – 180

2x² – 12x + 16 = 3x² – 12x – 180

3x² – 2x² – 12x + 12x – 180 – 16 = 0

x² – 196 = 0

x² = 196

x = √196

∴ x = ± 14

Question-18

(i) √(3x + 4) = x
(ii) √[x(x – 7)] = 3√2

Answer -18

(i) √(3x + 4) = x

3x + 4 = x²

( squaring  both sides,)

x² – 3x – 4 = 0

x² – 4x + x – 4 = 0

x(x – 4) + 1(x – 4) = 0

(x – 4) (x + 1) = 0

x – 4 = 0 or x + 1 = 0

x = 4 or x = -1

∴ Value of x = 4, -1

(ii) √[x(x – 7)] = 3√2

x(x – 7) = (3√2)²

(squaring on both sides)

x² – 7x = 9 × 2

x² – 7x – 18 = 0

x² – 9x + 2x – 18 = 0

x(x – 9) + 2(x – 9) = 0

(x – 9) (x + 2) = 0

x – 9 = 0 or x + 2 = 0

x = 9 or x = -2

Question-19

Use the substitution y = 3x + 1 to solve for x : 5(3x + 1 )² + 6(3x + 1) – 8 = 0

Answer-19

y = 3x + 1
Now, 5(3x + 1)² + 6(3x + 1) – 8 = 0

5y² + 6y – 8 = 0

5y² + 10y – 4y – 8 = 0

5y(y + 2) – 4(y + 2) = 0

(5y – 4) (y + 2) = 0

5y – 4 = 0 or y + 2 = 0

5y = 4 or y = -2

y = 4/5 or y = -2

3x + 1 = 4/5 or 3x + 1 = -2

3x = 4/5 – 1 or 3x = -2 – 1

3x = (4 – 5)/5 or 3x = -3

3x = -1/5 or x = -3/3

x = -1/15 or x = -1

Question -20 Find the values of x if p + 1 =0 and x² + px – 6 = 0

Answer-20

p + 1 = 0, then p = – 1
Substituting the value of p in the given quadratic equation
x² + ( – 1)x – 6 = 0
⇒ x² – x – 6 = 0
⇒ x² – 3x + 2x – 6 = 0
⇒ x (x – 3) + 2 (x – 3) = 0
⇒ (x – 3) (x + 2) = 0
Either x – 3 = 0, then x = 3
or x + 2 = 0, then x = – 2
Hence x = 3, -2

Question- 21 Find the values of x if p + 7 = 0, q – 12 = 0 and x² + px + q = 0,

Answer- 21

p + 7 = 0, then p = – 7
and q – 12 = 0, then q = 12
Substituting the values of p and q in the given quadratic equation,
x² – 7x + 12 = 0
⇒ x² – 3x – 4x + 12 = 0
⇒ x (x – 3) – 4 (x – 3) = 0
⇒ (x – 3) (x – 4) = 0
Either x – 3 = 0, then x = 3
or x – 4 = 0, then x = 4
Hence x = 3, 4

Question -22 If x = p is a solution of the equation x(2x + 5) = 3, then find the value of p.

Answer -22

Given, x = p and x(2x + 5) = 3
Substituting the value of p,
p(2p + 5) = 3
⇒ 2p² + 5p – 3 = 0
⇒ 2p² + 6p – p – 3 = 0

2p(p + 3) – 1(p + 3) = 0

(2p – 1) (p + 3) = 0

2p – 1 = 0 or p + 3 = 0

2p = 1 or p = -3

p = ½ or p = -3

Question-23 if x = 3 is a solution of equation …(k+2)x².-kx+6=0 find value of k hence find other root of equation

Answer-23   substituting x = 3 it must satisfy the equation

(k + 2)(3)² – k(3) + 6 = 0

(k + 2)(9) – 3k + 6 = 0

9k + 18 – 3k + 6 = 0

6k + 24 = 0

6(k + 4) = 0

So, k + 4 = 0

k = -4

putting k = -4

(-4 + 2)x² – (-4)x + 6 = 0

-2x² + 4x + 6 = 0

x² – 2x – 3 = 0

x² – 3x + x – 3 = 0

x(x – 3) + 1(x – 3) = 0

(x + 1)(x – 3) = 0

x + 1 = 0 or x – 3 = 0

— : End of ML Aggarwal Quadratic Equations Exe-5.2 Class 10 ICSE Maths Solutions :–

Return to :- ML Aggarwal Solutions for ICSE Class-10

Thanks

Please Share with Your Friends