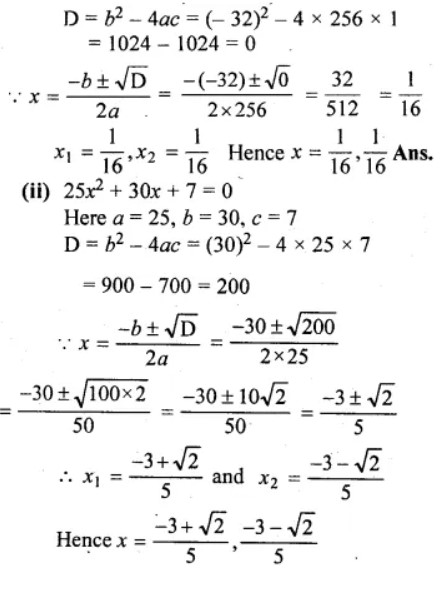ML Aggarwal Quadratic Equations Exe-5.3 Class 10 ICSE Maths Solutions. We Provide Step by Step Answer of Exe-5.3 Questions ( Using formula ) for Quadratic Equations in One Variable as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-10.
ML Aggarwal Ch-5 Quadratic Equations in one Variable Exercise- 5.3 Class 10 ICSE Maths Solutions
| Board | ICSE |
| Subject | Maths |
| Class | 9th |
| Chapter-5 | Quadratic Equations |
| Writer / Book | Understanding |
| Topics | Solutions of Exe-5.3 |
| Academic Session | 2024-2025 |
Quadratic Equations in one Variable Exe-5.3
(Class 10 ICSE ML Aggarwal Maths Solutions)
Question -1
(i) 2x² – 7x + 6 = 0
(ii) 2x² – 6x + 3 =0
Answer -1
let us consider,
a=2,b=-7,c=6
so ,by using the formula
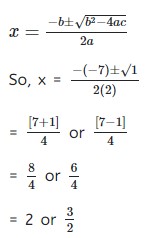
value of X = 2,OR 3/2
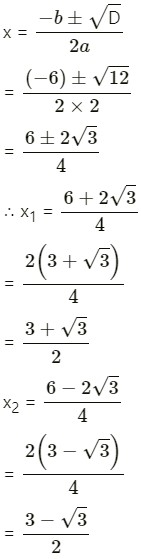
Question -2
(i) 256x² – 32x + 1 = 0
(ii) 25x² + 30x + 7 = 0
Answer-
Question-3
(i) 2x² + √5x – 5 = 0
(ii) √3x² + 10x – 8√3 = 0
Answer -3
(i) 2x² + √5x – 5 = 0
Here a = 2, b = √5, c = -5
using the formula
D = b2 – 4ac
= (√5)2 – 4(2) (-5)
= 5 + 40
= 45
x = [-(√5) ± √45] / 2(2)
= [-√5 ± 3√5)]/ 4
= [-√5 + 3√5)]/ 4 or [-√5 – 3√5]/ 4
= 2√5/4 or -4√5/4
= √5/2 or -√5
Let us consider,
a = √3, b = 10, c = -8√3
using the formula,
D = b2 – 4ac
= (10)2 – 4(√3) (-8√3)
= 100 + 96
= 196
x = [-(10) ± √196] / 2(√3)
= [-10 ± 14] / 2(√3)
= [-10 + 14)]/ 2√3 or [-10 – 14)]/ 2√3
= 4/2√3 or -24/2√3
Question-4
(i)( x-2)/(x+2)+(x+2)/( x-2)=4
(ii)( x +1)/(x+3)=(3x+2)/(2x+3)
Answer-4
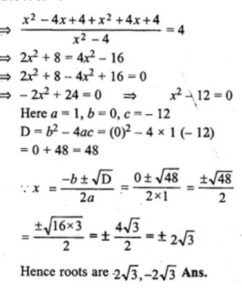
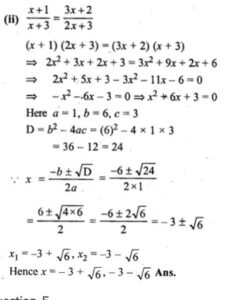
Question-5
(i) a (x² + 1) = (a² + 1) x , a ≠ 0
(ii) 4x² – 4ax + (a² – b²) = 0
Answer-5
(i) a (x² + 1) = (a² + 1) x
ax² – (a² + 1)x + a = 0
Let us consider,
a = a, b = -(a2 + 1), c = a
using the formula,
D = b2 – 4ac
= (-(a2 + 1))2 – 4(a) (a)
= a4 + 2a2 + 1 – 4a2
= a4 – 2a2 + 1
= (a2 – 1)2
putting value of D in formula
x = [-(-(a2 + 1)) ± √(a2 – 1)2] / 2(a)
= [(a2 + 1) ± (a2 – 1)] / 2a
= [(a2 + 1) + (a2 – 1)] / 2a or [(a2 + 1) – (a2 – 1)] / 2a
= [a2 + 1 + a2 – 1]/2a or [a2 + 1 – a2 + 1]/2a
= 2a2/2a or 2/2a
= a or 1/a
∴ Value of x = a, 1/a
(ii) 4x² – 4ax + (a² – b²) = 0
Let us consider,
a = 4, b = -4a, c = (a2 – b2)
using the formula,
D = b2 – 4ac
= (-4a)2 – 4(4) (a2 – b2)
= 16a2 – 16(a2 – b2)
= 16a2 – 16a2 + 16b2
= 16b2
putting value of D in formula
x = [-(-4a) ± √16b2] / 2(4)
= [4a ± 4b] / 8
= 4[a ± b] / 8
= [a ± b] / 2
= [a + b] / 2 or [a – b] / 2
∴ Value of x = [a + b] / 2, [a – b] / 2
Question-6
(i)x−1/x = 3, x ≠ 0
(ii)1/ x + 1/(x−2) = 3, x ≠ 0, 2
Answer-6
(i) x−1/x = 3, x ≠ 0
Let us simplify the given expression,
By taking LCM
x2 – 1 = 3x
x2 – 3x – 1 = 0
Let us consider,
a = 1, b = -3, c = -1
using the formula,
D = b2 – 4ac
= (-3)2 – 4(1) (-1)
= 9 + 4
= 13
Putting Value of D in Formula
x = [-(-3) ± √13] / 2(1)
= [3 ± √13] / 2
= [3 + √13] / 2 or [3 – √13] / 2
∴ Value of x = [3 + √13] / 2 or [3 – √13] / 2
(ii) 1/ x + 1/(x−2) = 3, x ≠ 0, 2
[(x – 2) + x] / [x(x – 2)] = 3
[x – 2 + x] / [x2 – 2x] = 3
2x – 2 = 3(x2 – 2x)
2x – 2 = 3x2 – 6x
3x2 – 6x – 2x + 2 = 0
3x2 – 8x + 2
a = 3, b = -8, c = 2
using the formula,
D = b2 – 4ac
= (-8)2 – 4(3) (2)
= 64 – 24
= 40
Putting value of D in formula
x = [-(-8) ± √40] / 2(3)
= [8 ± 2√10] / 6
= 2[4 ± √10] / 6
= [4 ± √10] / 3
= [4 + √10] / 3 or [4 – √10] / 3
∴ Value of x = [4 + √10] / 3 or [4 – √10] / 3
Question-7 Solve for x
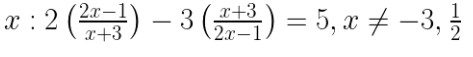
Answer-7
Let (2x-1 )/(x+3) = x
then (x+3)/ (2x-1) = 1/x
2x – 3/x = 5
2x2 – 3 = 5x
2x2 – 5x – 3 = 0
a = 2, b = -5, c = -3
using the formula,
D = b2 – 4ac
= (-5)2 – 4(2) (-3)
= 25 + 24
= 49
Putting value of D in equation
x = [-(-5) ± √49] / 2(2)
= [5 ± 7] / 4
= [5 + 7] / 4 or [5 – 7] / 4
= [12]/4 or [-2]/4
= 3 or -1/2
So, x = 3 or -1/2
When x = 3, then
(2x-1) / (x+3) = 3
2x – 1 = 3x + 9
3x + 9 – 2x + 1 = 0
x + 10 = 0
x = -10
When x = -1/2, then
(2x-1) / (x+3) = -1/2
2(2x – 1) = -(x + 3)
4x – 2 = -x – 3
4x – 2 + x + 3 = 0
5x + 1 = 0
5x = -1
x = -1/5
∴ Value of x = -10, -1/5
Question -8 Solve the following equation by using quadratic equations for x and give your
(i) x² – 5x – 10 = 0
(ii) x² + 7x = 7
Answer -8
(i) x² – 5x – 10 = 0
On comparing with, ax² + bx + c = 0
a = 1, b = -5, c = -10
using the formula,
D = b2 – 4ac
= (-5)2 – 4(1) (-10)
= 25 + 40
= 65
putting value of D in equation
x = [-(-5) ± √65] / 2(1)
= [5 ± √65] / 2
= [5 ± 8.06] / 2
= [5 + 8.06] / 2 or [5 – 8.06] / 2
= [13.06]/2 or [-3.06]/2
= 6.53 or -1.53
∴ Value of x = 6.53 or -1.53
(ii) x2 + 7x = 7
x2 + 7x – 7 = 0
Let us consider,
a = 1, b = 7, c = -7
using the formula,
D = b2 – 4ac
= (7)2 – 4(1) (-7)
= 49 + 28
= 77
Putting value of D in equation
x = [-7 ± √77] / 2(1)
= [-7 ± 8.77] / 2
= [-7 + 8.77] / 2 or [-7 – 8.77] / 2
= 1.77/2 or -15.77/2
= 0.885 or -7.885
Question-9 Solve the following equations by using quadratic formula and give your answer correct to 2 decimal places :
(i) 4x² – 5x – 3 = 0
(ii) 2x – 1/x = 7
Answer-9
(i) Given equation 4x² – 5x – 3 = 0
Comparing with ax² + bx + c = 0, we have
a = 4, b = -5, c = -3
using the formula,
D = b2 – 4ac
= (-5)2 – 4(4) (-3)
= 25 + 48
= 73
Putting value of D in equation
x = [-(-5) ± √73] / 2(4)
= [5 ± 8.54] / 8
= [5 + 8.54] / 8 or [5 – 8.54] / 8
= 13.54/8 or -3.54/8
= 1.6925 or -0.4425
∴ Value of x = 1.69 or -0.44
(ii) 2x – 1/x = 7
2x2 – 1 = 7x
2x2 – 7x – 1 = 0
a = 2, b = -7, c = -1
using the formula,
D = b2 – 4ac
= (-7)2 – 4(2) (-1)
= 49 + 8
= 57
Putting value of D in equation
x = [-(-7) ± √57] / 2(2)
= [7 ± 7.549] / 4
= [7 + 7.549] / 4 or [7 – 7.549] / 4
= 14.549/4 or -0.549/4
= 3.637 or -0.137
= 3.64 or -0.14
Question-10 Solve for x the quadratic equation Give your answer correct to three significant figures.
(i ) x2 – 4x – 8 = 0.
(ii) x – 18/x = 6.
Answer-10
(i) Given equation:
x2 – 4x – 8 = 0
on comparing
a = 1, b = -4, c = -8
using the formula,
D = b2 – 4ac
= (-4)2 – 4(1) (-8)
= 16 + 32
= 48
Putting value of D in equation
x = [-(-4) ± √48] / 2(1)
= [4 ± 6.93]/2
= [4 + 6.93]/2 or [4 – 6.93]/2
= [10.93]/2 or -2.93/2
= 5.465 or -1.465
(ii)
x−18/x = 6
x2 – 18 = 6x
x2 – 6x – 18 = 0
a = 1, b = -6, c = -18
using the formula,
D = b2 – 4ac
= (-6)2 – 4(1) (-18)
= 36 + 72
= 108
putting value of D in equation
x = [-(-6) ± √108] / 2(1)
= [6 ± 10.39]/2
= [6 + 10.39]/2 or [6 – 10.39]/2
= [16.39]/2 or -4.39/2
= 8.19 or -2.19
Question- 11 Solve the equation 5x² – 3x – 4 = 0 and give your answer correct to 3 significant figures:
Answer-11
We have 5x² – 3x – 4 = 0
Here a = 5, b = – 3, c = – 4
using the formula,
D = b2 – 4ac
= (-3)2 – 4(5) (-4)
= 9 + 80
= 89
Putting value of D in equation
x = [-(-3) ± √89] / 2(5)
= [3 ± 9.43] / 10
= [3 + 9.43] / 10 or [3 – 9.43] / 10
= 12.433/10 or -6.43/10
= 1.24 or -0.643
— : End of ML Aggarwal Quadratic Equations Exe-5.3 Class 10 ICSE Maths Solutions :–
Return to :- ML Aggarwal Solutions for ICSE Class-10
Thanks
Please Share with Your Friends