ML Aggarwal Quadratic Equations MCQs Class 10 ICSE Maths Solutions

ML Aggarwal Quadratic Equations MCQs Class 10 ICSE Maths Solutions  Ch-5. We Provide Step by Step Answer of MCQs Questions for Quadratic Equations in One Variable as council prescribe guideline for upcoming board exam. Visit official Website  CISCE  for detail information about ICSE Board Class-10.

ML Aggarwal Ch-5 Quadratic Equations in one Variable MCQs Class 10 ICSE Maths Solutions

Board	ICSE
Subject	Maths
Class	9th
Chapter-5	Quadratic Equations
Writer / Book	Understanding
Topics	Solutions of MCQs
Academic Session	2024-2025

Ch-5 Quadratic Equations in one Variable MCQs

(Class 10 ICSE ML Aggarwal Maths Solutions)

Choose the correct answer from the given four options (1 to 10) :

Question -1 Which of the following is not a quadratic equation ?
(a) (x + 2)² = 2(x + 3)
(b) x² + 3x = ( – 1) (1 – 3x)
(c) (x + 2) (x – 1) = x² – 2x – 3
(d) x³ – x² + 2x + 1 = (x + 1)³

Answer -1

(a) (x + 2)² = 2(x + 3)
⇒ x² + 4x + 4 = 2x + 6
⇒ x² + 4x – 2x + 4 – 6 = 0
⇒ x² + 2x – 2
It is a quadratic equation.

(b) x² + 3x = ( – 1) (1 – 3x)
⇒ x² + 3x = –1 + 3x
⇒ x² + 1 = 0
it is also quadratic equation.

(c)(x + 2) (x – 1) = x² – 2x – 3

x² – x + 2x – 2 = x² – 2x – 3
x² – x² + x + 2x – 2 + 3 = 0
⇒ 3x + 1 = 0
It is not a quadratic equation.

(d) x³ – x² + 2x + 1 = (x + 1)³ 

= x³ + 3x² + 3x + 1
x³ – x² + 2x + 1
3x² + x² – 2x – 1 + 3x + 1 = 0
⇒ 4x² + x = 0
It is a quadratic equation

Question- 2 If 1/2 is a root of the quadratic equation 4x² – 4kx + k + 5 = 0, then the value of k is
(a) – 6
(b) – 3
(c) 3
(d) 6

Answer-2

12 is a root of the equation
4x² – 4kx + k + 5 = 0

Substituting the value of x = 1/2 in the equation

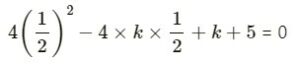
1 – 2k + k + 5 = 0
⇒ – k + 6 = 0
k = 6.

Question-3 The roots of the equation x² – 3x – 10 = 0 are
(a) 2,- 5
(b) – 2, 5
(c) 2, 5
(d) – 2, – 5

Answer-3

x² – 3x – 10 = 0

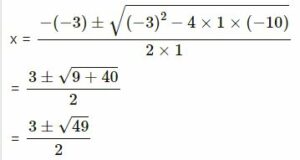
either

= (3+7)/ 2

∴ x = 10/2 = 5
or
x = (3-7)/2

=-4/2 = –2

x = 5, – 2 or – 2, 5 (b)

Question-4 If one root of a quadratic equation with rational coefficients is (3- √5) / 2, then the other

(a) (-3 – √5)/2

(b) (- 3+ √5)/2

(c) (3+ √5)/2
(d)  ( √3+ 5)/2             

Answer-4 One root of a quadratic equation is (3- √5)/2, then other root will be (3+ √5)/2, (c)

Question-5 If the equation 2x² – 5x + (k + 3) = 0 has equal roots then the value of k is
(a)9/8
(b)-9/8
(c)1/8
(d)-1/8

Answer-5

2x² – 5x + (k + 3) = 0
a = 2, b = –5, c = k + 3
∴ b² – 4ac
= (–5)² – 4 x 2 x (k + 3)
= 25 – 8(k + 3)
∴ Roots are equal.
∴ b² – 4ac = 0
∴ 25 – 8(k + 3) = 0
25 – 8k – 24 = 0
1 – 8k = 0
⇒ 8k = 1

∴ k = 1/8.

Question-6 The value(s) of k for which the quadratic equation 2x² – kx + k = 0 has equal roots is (are)
(a) 0 only
(b) 4
(c) 8 only
(d) 0, 8

Answer-6

2x² – kx + k = 0
a = 2, b = -k, c = k
∴ b² – 4ac
= (-k)² – 4 x 2 x 4
= k² – 8k
∴ Roots are equal.
∴ b² – 4ac = 0
k² – 8k = 0
⇒ k(k – 8) = 0
Either k = 0
or k – 8 = 0,
then k = 8
k = 0, 8.
So option (d) is correct

Question-7 If the equation 3x² – kx + 2k =0 roots, then the the value(s) of k is (are)
(a) 6
(b) 0 Only
(c) 24 only
(d) 0

Answer -7

3x² – kx + 2k = 0
Here, a = 3, b = -k, c = 2k
b² – 4ac
= (–k)² – 4 x 3 x 2k
= k² – 24k
∴ Roots are equal.
∴ b² – 4ac = 0
∴ k² – 24k = 0
⇒ k(k – 24) = 0
Either k = 0
or
k – 24 = 0,
then k = 24
∴ k = 0, 24.

Question -8 If the equation {k + 1)x² – 2(k – 1)x + 1 = 0 has equal roots, then the values of k are
(a) 1, 3
(b) 0, 3
(c) 0, 1
(d) 0, 1

Answer -8

(k + 1)x² – 2(k – 1)x + 1 = 0
Here, a = k + 1, b = -2(k – 1), c = 1
∴ b² – 4ac
= [–2(k –- 1)]² – 4(k + 1)(1)
= 4(k² – 2k + 1) – 4k – 4
= 4k² – 8k + 4 – 4k – 4
= 4k² – 12k
∵ Roots are equal.
∴ b² – 4ac = 0
∴ 4k² – 12k = 0
4k(k – 3) = 0
⇒ 4k(k – 3) = 0
⇒ k(k – 3) = 0
Either k = 0
or
k – 3 = 0,
then k = 3
k = 0, 3

Option (b) is correct

Question-9 If the equation 2x² – 6x + p = 0 has real and different roots, then the values of p are given by
(a)p < 9/2
(b)p ≤ 9/2
(c)p > 9/2
(d)p ≥ 9/2

Answer-9

2x² – 6x + p = 0
Here, a = 2, b = -6, c = p

b² – 4ac
= (–6)² – 4 x 2 x p
= 36 – 8p
∵ Roots are real and unequal.
∴ b² – 4ac > 0
⇒ 36 – 8p > 0
⇒ 36 > 8p

⇒ 36/8 > p

⇒ p < 36/8

⇒ p < 9/2.

Question-10 The quadratic equation 2x² – √5x + 1 = 0 has
(a) two distinct real roots
(b) two equal real roots
(c) no real roots
(d) more than two real roots

Answer -10

2x² – √5x + 1 = 0
Here, a = 2, b = -√5, c = 1
b² – 4ac

= (-√5)² -4×2 x1
= 5 – 8
= -3
∵ b² – 4ac < 0
∴ It has no real roots.

So option (c) is correct

—  : End of ML Aggarwal Quadratic Equations MCQs Class 10 ICSE Maths Solutions : –

Return to :- ML Aggarwal Solutions for ICSE Class-10

Thanks

Please Share with Your Friends