ML Aggarwal Quadrilaterals Shapes Check Your Progress Class 8 ICSE Ch-13 Maths Solutions. We Provide Step by Step Answer of Check Your Progress Questions for Quadrilaterals Shapes as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-8.
ML Aggarwal Quadrilaterals Shapes Check Your Progress Class 8 ICSE Maths Solutions
| Board | ICSE |
| Publications | Avichal Publishig Company (APC) |
| Subject | Maths |
| Class | 8th |
| Chapter-13 | Quadrilaterals Shapes |
| Writer | ML Aggarwal |
| Book Name | Understanding |
| Topics | Solution of Check Your Progress Questions |
| Edition | 2023-2024 |
Quadrilaterals Shapes Check Your Progress
ML Aggarwal Class 8 ICSE Maths Solutions
Page-249
Question 1. From the given diagram, find the value of x.
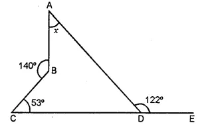
Answer:
Reflex angle B = 360 – 140 = 220°
Also, ∠ADC = 180 – 122 = 58° (Linear pair)
Now, ABCD is a quadrilateral
∴ ∠A + ∠B + ∠C + ∠D = 360°
⇒ x + 220 + 53 + 58 = 360
or x = 360 – 331 =29°
Quadrilaterals Shapes Check Your Progress
ML Aggarwal Class 8 ICSE Maths Solutions
Page-250
Question 2. If two angles of a quadrilateral are 77° and 51°, and out of the remaining two angles, one angle is 10° smaller than the other, find these angles.
Answer
Two angles of a quadrilateral are 77° and 51°
Sum of angles of a quadrilateral = 360°
∴ Sum of other two angles = 360° – (77° + 51°)
= 360° – 134° = 226°
Let one angle among there two angles = x
Then other angle = x – 10°
∴ x + x – 10 = 226°
⇒ 2x = 226° + 10° = 236°
⇒ x = 236°/2 = 118°
∴ One angle = 118°
and other angle =118 – 10 = 108°
Question 3. In the given figure, AB || DC, ∠A = 74° and ∠B : ∠C = 4 : 5. Find
(i) ∠D
(ii) ∠B
(iii) ∠C
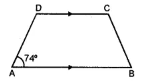
Answer:
∠A = 74° ∠B = 4x, ∠C = 5x.
As AB || CD
∴ 4x + 5x= 180°, 9x= 180°
⇒ x = 20°
∴ ∠B = 80° and ∠C = 100°
ABCD is a quadrilateral
∴ ∠A + ∠B + ∠C + ∠D = 360°
⇒ ∠D = 360° – (74° + 80° + 100°)
= 360°- 254 = 106°
Therefore, ∠D = 106° ∠B = 80°, ∠C = 100°
Question 4. In quadrilateral ABCD, ∠A : ∠B : ∠C : ∠D = 3 : 4 : 6 : 7. Find all the angles of the quadrilateral. Hence, prove that AB and DC are parallel. Is BC also parallel to AD?
Answer:
Let, four angles of quadrilateral be 3x, 4x, 6x, 7x.
∴ 3x + 4x + 6x + 7x = 360
20x = 360 ⇒ x = 18
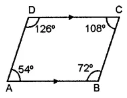
∴ ∠A = 3x = 3 × 18 = 54°
∠B = 4x = 4 × 18 = 72°
∠C = 6x = 6 × 18= 108°
∠D = 7x = 7 × 18= 126°
As, ∠A + ∠D = 54 + 126 = 180°
∴ AB || CD
(If two angles on the same side of transversal are supplementary,
then lines are parallel)
But ∠A + ∠B (54 + 72) ≠ 180
∴ BC is not parallel to AD.
Question 5. One angle of a parallelogram is two-third of the other. Find the angles of the parallelogram.
Answer:
In a parallelogram, one angle is 2/3 of the other.
Let one angle = x
Then second = 2/3x
But x + 2/3x = 180°
⇒ 5/3 = 180°
⇒ x =108° x 3/5 = 108°
∴ ∠A = x = 108°
∠B = 2/3x = 108° × 2/3 =72°
But ∠C = ∠A and ∠D = ∠B
(Opposite angles of a parallelogram)
∴∠C = ∠A = 108° and ∠D = ∠B = 72°
Hence, ∠A = 108°, ∠B = 72°, ∠C = 108°, ∠D = 72°
Question 6. In the given figure, ABCD is a kite. If ∠BCD = 52° and ∠ADB = 42°, find the values of x, y, and z.
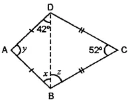
Answer:
Join BD.
In ∆ ABD,
AB = AD (Given)
∴ ∠ABD = ∠ADB
(angles opposite to equal sides are equal)
⇒ x = 42°
In ∆ BCD,
BC = CD (given)
∴ ∠BDC = ∠DBC = z
∴ z + z + 52 = 180° ⇒ 2z = 128
⇒ z = 64°
ABCD is quadrilateral
∴ ∠A + ∠B + ∠C + ∠D = 360°
⇒ y + (x + z) + 52 + (42 + z) = 360°
⇒ y + 106 + 52 + 106 = 360
⇒ y = 360 – 264 = 96°
Question 7. In the given figure, ABCD is a rectangle. Prove that AC = BD.
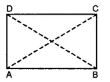
Answer:
In ∆ ABC and ∆ABD
BC = AD (opposite sides of rectangle)
∠B = ∠A (each 90°)
AB = AB (common)
∴ ∆ABC = ∆ABD (S.A.S.)
∴ AC ≅ BD (c.p.c.t.)
Question 8. In the given figure, ABCD is a rhombus and EDC is an equilateral triangle. If ∠DAB = 48°, find
(i) ∠BEC
(ii) ∠DEB
(iii) ∠BFC
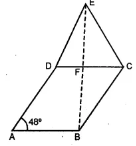
Answer:
ABCD is a rhombus
∴ AB = BC = CD = DA
Also, EDC is an equilateral ∆
∴ ED = DC = CE …(ii)
From (i) and (ii)
We get, BC = CE.
In ∆ BCE, ∠BCE = 60 + 48 = 108
Also, BC = EC
∴ ∠BEC = ∠EBC = x
⇒ x + x + ∠BCE = 180°
⇒ 2x = 180 – 108 = 72°
⇒ x = 36°
∴ ∠BEC = x = 36°.
(ii) ∠DEB = ∠DEC – ∠BEC
= 60° – 36° = 24°
(iii) In ∆ DEF,
∠D = 60°, ∠DEF = 24°, ∠DFE = y.
60 + 24 + 7 = 180°
y = 180 – 84 = 96°
∠BFC = ∠DFE = 96° (Vertically opposite angles)
Question 9. Find the number of sides of a regular polygon if each of its interior angle is 168°.
Answer:
Each interior angle of a regular polygon = 168°
Let number of sides = n, then (2n – 4)/n × 90° = 168°
(2n – 4)/n = 168/90 = 28/15
∴ 30n – 60 = 28n
⇒ 30n – 28n = 60
⇒ 2n = 60
⇒ n = 60/2 = 30
∴ Number of sides of the polygon = 30
Question 10. If the sum of interior angles of polygon is 3780° find the number of sides.
Answer
Sum of interior angles of polygon = (2n – 4) × 90
∴ 3780 = (2n – 4) × 90 ⇒ (2n – 4) =3780/90
⇒ 2n – 4 = 42
⇒ 2n = 46
⇒ n = 23
Question 11. The angles of a hexagon are (2x + 5)°, (3x – 5)°, (x + 40)°, (2x + 20)°, (2x + 25)° and (2x + 35)°. Find the value of x.
Answer:
Number of sides in hexagon = 6.
Sum of interior angles = (2 × 6 – 4) × 90 = 720°
∴ (2x + 5) + (3x – 5) + (x + 40) + (2x + 20)
+ (2x + 25) + (2x + 35) = 720
⇒ 12x + 120 = 720
⇒ 12x = 720 – 120
⇒ 12x = 600
⇒ x = 50.
Question 12. Two angles of a polygon are right angles and every other angle is 120°. Find the number of sides of the polygon.
Answer:
Let the number of sides = n
∴ 2 × 90 + (n – 2) × 120 = (2n – 4) × 90
⇒ 180 + 120n – 240 = 180n – 360
⇒ 120n – 60 = 180n – 360
⇒ 60n = 300
⇒ n = 5
Question 13. The sum of interior angles of a regular polygon is twice the sum of its exterior angles. Find the number of sides of the polygon.
Answer:
Sum of interior angles = (2n – 4) × 90
Sum of exterior angles = 360
According to the condition,
(2n – 4) × 90 = 2 × 360
⇒ 2n – 4 = 8
∴ n = 6
Question 14. An exterior angle of a regular polygon is one- fourth of its interior angle. Find the number of sides in the polygon.
Answer:
Let measure of interior angle = x°
Then exterior angle = 1/4x°
∴ x + 1/4x = 180° ⇒ 5/4 x = 180
⇒ x = 180 × 4/5 ⇒ x = 144°
Therefore, each interior angle is 144°
144 = (2n – 4)/n x 90
⇒ 144n= 180n – 360
⇒ 180n – 144n = 360
⇒ 36n = 360
⇒ n = 10
— End of Quadrilaterals Shapes Check Your Progress Class 8 ICSE Maths Solutions :–
Return to : – ML Aggarwal Maths Solutions for ICSE Class -8
Thanks


