ML Aggarwal Quadrilaterals Shapes Exe-13.2 Class 8 ICSE Ch-13 Maths Solutions

ML Aggarwal Quadrilaterals Shapes Exe-13.2 Class 8 ICSE Ch-13 Maths Solutions. We Provide Step by Step Answer of  Exe-13.2 Questions for Quadrilaterals Shapes as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-8.

ML Aggarwal Quadrilaterals Shapes Exe-13.2 Class 8 ICSE Maths Solutions

Board	ICSE
Publications	Avichal Publishig Company (APC)
Subject	Maths
Class	8th
Chapter-13	Quadrilaterals Shapes
Writer	ML Aggarwal
Book Name	Understanding
Topics	Solution of Exe-13.2 Questions
Edition	2023-2024

Quadrilaterals Shapes Exe-13.2

ML Aggarwal Class 8 ICSE Maths Solutions

Page-237

Question 1. In the given figure, ABCD is a parallelogram. Complete each statement along with the definition or property used.

(i) AD = ………..
(ii) DC = ………..
(iii) ∠DCB = ………..
(iv) ∠ADC = ………..
(v) ∠DAB = ………..
(vi) OC = ………..
(vii) OB = ………..
(viii) m∠DAB + m∠CDA = ………..

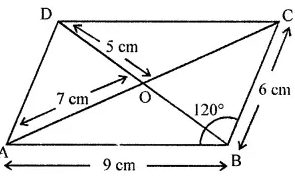
Answer:

In paralleloram ABCD
(i) AD = 6 cm (Opposite sides of parallelogram)
(ii) DC = 9 cm (Opposite sides of parallelogram)
(iii) ∠DCB = 60° (∵ ∠DCB + ∠CBA = 180°)
(iv) ∠ADC = ∠ABC = 120°
(v) ∠DAB = ∠DCB = 60°
(vi) OC = AO = 7 cm
(vii) OB = OD = 5 cm
(viii) m∠DAB + m∠CDA = 180°

---

Quadrilaterals Shapes Exe-13.2

ML Aggarwal Class 8 ICSE Maths Solutions

Page-238

Question 2. Consider the following parallelograms. Find the values of x, y, z in each.

Answer:

(i)

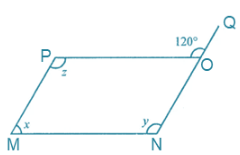
From the figure, ∠POQ = 120^o

Sum of angles linear pair is equal to 180^o

So, ∠POQ + ∠PON = 180^o

120^o + ∠PON = 180^o

∠PON = 180^o – 120^o

∠PON = 60^o

∠M = ∠O = 60^o … [because opposite angles of parallelogram are equal]

∠POQ = ∠MNO

120^o = 120^o … [because corresponding angels are equal]

y = 120^o

z = y

120^o = 120^o

Hence, x = 60^o, y = 120^o and z = 120^o

(ii)

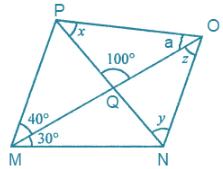
From the figure, it is given that ∠PQO = 100^o, ∠OMN = 30^o, ∠PMO =40^o.

Then, ∠NOM = ∠OMP … [because alternate angles are equal]

So, z = 40^o

Now, ∠NMO = ∠POM … [because alternate angles are equal]

So, ∠NMO = a = 30^o

Consider the triangle PQO,

Sum of measures of interior angles of triangle is equal to 180^o.

∠P + ∠Q + ∠O = 180^o

x + 100^o + 30^o = 180^o

x + 130^o = 180^o

x = 180^o – 130^o

x = 50^o

Then, exterior angle ∠OQP = y + z

100^o = y + 40^o

By transposing we get,

y = 100^o – 40^o

y = 60^o

Hence, the value of x = 50^o, y = 60^o and z = 40^o.

(iii) 

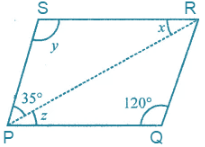
∠SPR = ∠PRQ

35^o = 35^o … [because alternate angles are equal]

Now consider the triangle PQR,

Sum of measures of interior angles of triangle is equal to 180^o.

∠RPQ + ∠PQR + ∠PRQ = 180^o

z + 120^o + 35^o = 180^o

z + 155^o = 180^o

z = 180^o – 155^o

z = 25^o

Then, ∠QPR = ∠PRQ

Z = x

25^o = 25^o … [because alternate angles are equal]

in parallelogram opposite angles are equal.

So, ∠S = ∠Q

y = 120^o

Hence, value of x = 25^o, y = 120^o and ∠z = 25^o.

(iv)

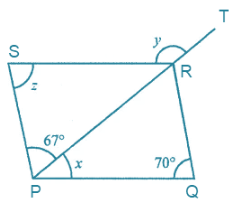
From the figure, it is given that ∠SPR = 67^o and ∠PQR = 70^o

∠SPR = ∠PRQ

67^o = 67^o … [because alternate angles are equal]

Now, consider the triangle PQR

sum of measures of interior angles of triangle is equal to 180^o.

∠RPQ + ∠PQR + ∠PRQ = 180^o

x + 70^o + 67^o = 180^o

x + 137^o = 180^o

x = 180^o – 137^o

x = 43^o

Then, ∠PSR = ∠PQR

We know that, in parallelogram opposite angles are equal.

Z = 70^o

Also we know that, exterior angle ∠SRT = ∠PSR + ∠SPR

y = 70^o + 67^o

y = 137^o

Hence, value of x = 43^o, y = 137^o and z = 70^o

Question 3. Two adjacent sides of a parallelogram are in the ratio 5 : 7. If the perimeter of parallelogram is 72 cm, find the length of its sides.

Answer:

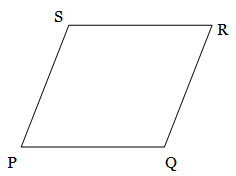
Consider the parallelogram PQRS,

From the question it is given that, two adjacent sides of a parallelogram are in the ratio 5 : 7.

Perimeter of parallelogram = 72 cm

2(SP + RQ) = 72 cm

SP + RQ = 72/2

SP + RQ = 36 cm

Let us assume the length of side SP = 5y and RQ = 7y,

5y + 7y = 36

12y = 36

y = 36/12

y = 3

Therefore, SP = 5y = 5 × 3 = 15 cm

RQ = 7y = 7 × 3 = 21 cm

Question 4. The measure of two adjacent angles of a parallelogram are in the ratio 4 : 5. Find the measure of each angle of the parallelogram.

Answer:

Consider the parallelogram PQRS,

From the question it is given that, The measure of two adjacent angles of a parallelogram is in the ratio 4 : 5.

So, ∠P: ∠Q = 4: 5

Let us assume the ∠P = 4y and ∠Q = 5y.

∠P + ∠Q = 180^o

4y + 5y = 180^o

9y = 180^o

y = 180^o/9

y = 20^o

Hence, ∠P = 4y = 4 × 20^o = 80^o and ∠Q = 5y = (5 × 20^o) = 100^o

In parallelogram opposite angles are equal,

So, ∠R = ∠P = 80^o

∠S = ∠Q = 100^o

Question 5. Can a quadrilateral ABCD be a parallelogram, give reasons in support of your answer.

(i) ∠A + ∠C= 180°?
(ii) AD = BC = 6 cm, AB = 5 cm, DC = 4.5 cm?
(iii) ∠B = 80°, ∠D = 70°?
(iv) ∠B + ∠C= 180°?

Answer:

From the question it is given that, quadrilateral ABCD can be a parallelogram.

In parallelogram opposite sides are equal and opposites angles are equal.

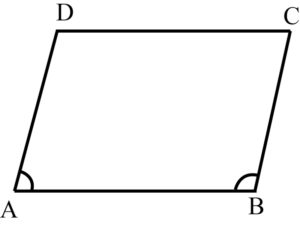
So, AB = DC and AD = BC also ∠A = ∠C and ∠B = ∠D.

(i) ∠A + ∠C= 180^o

From the above condition it may be a parallelogram and may not be a parallelogram.

(ii) AD = BC = 6 cm, AB = 5 cm, DC = 4.5 cm

From the above dimension not able to form parallelogram.

Because AB ≠ DC

(iii) ∠B = 80^o, ∠D = 70^o

From the above dimension not able to form parallelogram.

Because ∠B ≠ ∠D

(iv) ∠B + ∠C= 180^o

From the above condition it may be a parallelogram and may not be a parallelogram.

Question 6. In the following figures HOPE and ROPE are parallelograms. Find the measures of angles x, y and z. State the properties you use to find them.

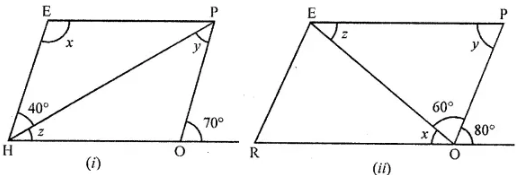
Answer:

(i) In parallelogram HOPE, HO is produced to D

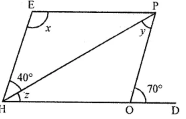
∠AOP + ∠POD = 180° (Linear pair)
∴ ∠AOP + 70°= 180°
∠AOP = 180°- 70°= 110°
But ∠AOP = ∠HEP (Opposite angles of a ||gm)
∠HEP = 110°
⇒ x = 110°
∠HPO = ∠EHP (Alternate angles)
∴ y = 40°
In ∆HOP, Ext. ∠POD = y + z
⇒ 70° = y + z
⇒ 70° = 40° + z
⇒ z = 70° – 40° = 30°
∴ x= 110°, y = 40°, z = 30°

(ii) In ||gm ROPE, RO is produced to D

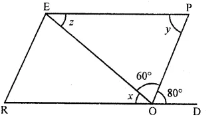
∠POD = 80°, ∠EOP = 60°
∠P = ∠POD (Alternate angles)
∴ y = 80°
∠ROE + ∠EOP + ∠POD = 180° (Angles on one side of a line)
x + 60° + 80° = 180° ⇒ x + 140° = 180°
∴ x = 180°- 140° = 40°
z = x (Alternate angles)
∴ z = 40°
Hence, x = 40°, y = 80°, z = 40°

---

Quadrilaterals Shapes Exe-13.2

ML Aggarwal Class 8 ICSE Maths Solutions

Page-239

Question 7. In the given figure TURN and BURN are parallelograms. Find the measures of x and y (lengths are in cm).

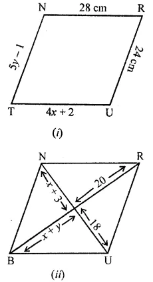
Answer:

(i) Consider the parallelogram TURN

In parallelogram opposite sides are equal.

So, TU = RN

4x + 2 = 28

4x = 28 – 2

4x = 26

x = 26/4

x = 6.5 cm

and NT = RU

5y – 1 = 24

5y = 24 + 1

5y = 25

y = 25/5

y = 5

Hence, value of x = 6.5 cm and y = 5 cm.

(ii) Consider the parallelogram BURN,

BO = OR

x + y = 20 … [equation (i)]

UO = ON

x + 3 = 18

x = 18 – 3

x = 15

substitute the value of x in equation (i),

15 + y = 20

y = 20 – 15

y = 5

Hence, value of x = 15 and y = 5.

Question 8. In the following figure both ABCD and PQRS are parallelograms. Find the value of x.

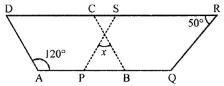
Answer:

Two parallelograms ABCD and PQRS in which
∠A = 120° and ∠R = 50°
∠A + ∠B = 180° (Co-interior angles)
120° + ∠B = 180°

⇒ ∠B = 180°- 120° = 60°
∠P = ∠R (Opposite angles of a ||gm)
∠P = 50°
Now in ∆OPB,
∠POB + ∠P + ∠B = 180° (Angles of a triangle)
x + 50° + 60° = 180°
x + 110° = 180° ⇒ x = 180°- 110° = 70°
∴ x = 70°

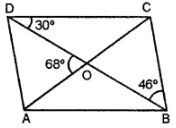
Question 9. In the given figure, ABCD, is a parallelogram and diagonals intersect at O. Find :

(i) ∠CAD
(ii) ∠ACD
(iii) ∠ADC

Answer:

(i) ∠DBC = ∠BDA = 46° (alternate angles)
In ∆ AOD,
46° + 68° + ∠CAD = 180° (∵ ∠CAD = ∠OAD)
∠CAD = 180°- 114° = 66°
(ii) ∠AOD + ∠COD = 180° (straight angle)
∴ ∠COD= 180°- 68°= 112°
In ∆COD, 112° + 30° + ∠ACD = 180° (∵ ∠ACD = ∠OCD)
∠ACD = 180° – 112° – 30° = 38°
(iii) ∠ADC = 30° + 46° = 76° (∵ ∠ADC = ∠ADO + ∠ODC)

(ML Aggarwal Quadrilaterals Shapes Exe-13.2 Class 8 ICSE Maths)

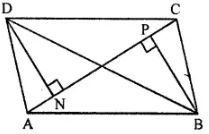
Question 10. In the given figure, ABCD is a parallelogram. Perpendiculars DN and BP are drawn on diagonal AC. Prove that:

(i) ∆DCN ≅ ∆BAP
(ii) AN = CP

Answer:

In the given figure,
ABCD is a parallelogram AC is it’s one diagonal.
BP and DN are perpendiculars on AC.
To prove :
(i) ∆DCN ≅ ∆BAP
(ii) AN = CP
Proof: In ∆DCN and ∆BAP
DC=AB (Opposite sides of a ||gm)
∠N = ∠P (Each 90°)
∠DCN = ∠PAB (Alternate angle)
∴ ∆DCN ≅ ∆BAP (AAS axiom)
∴ NC = AP (c.p.c.t.)
Subtracting NP from both sides.
NC – NP = AP – NP
∴ AN = CP

Question 11. In the given figure, ABC is a triangle. Through A, B and C lines are drawn parallel to BC, CA and AB respectively, which forms a ∆PQR. Show that
2(AB + BC + CA) = PQ + QR + RP.

Answer:

From the figure it is given that,

Through A, B and C lines are drawn parallel to BC, CA and AB respectively.

We have to show that 2(AB + BC + CA) = PQ + QR + RP

Then, AB ∥ RC and AR ∥ CB

ABCR is a parallelogram.

So, AB = CR … [equation (i)]

CB = AR … [equation (ii)]

ABPC is a parallelogram.

AB ∥ CP and PB ∥ CA

AB = PC … [equation (iii)]

AC = PB … [equation (iv)]

ACBQ is a parallelogram

AC = BQ … [equation (v)]

AQ = BC … [equation (vi)]

By adding all the equation,

AB + AB + BC + BC + AC + AC = PB + PC + CR + AR + BQ +BC

2AB + 2BC + 2AC = PQ + QR + RP

By taking common

2(AB + BC + AC) = PQ + QR + RP

— End of Quadrilaterals Shapes Exe-13.2 Class 8 ICSE Maths Solutions :–

Return to : – ML Aggarwal Maths Solutions for ICSE Class -8

Thanks