ML Aggarwal Quadrilaterals Shapes Exe-13.3 Class 8 ICSE Ch-13 Maths Solutions

ML Aggarwal Quadrilaterals Shapes Exe-13.3 Class 8 ICSE Ch-13 Maths Solutions. We Provide Step by Step Answer of  Exe-13.3 Questions for Quadrilaterals Shapes as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-8.

ML Aggarwal Quadrilaterals Shapes Exe-13.3 Class 8 ICSE Maths Solutions

Board	ICSE
Publications	Avichal Publishig Company (APC)
Subject	Maths
Class	8th
Chapter-13	Quadrilaterals Shapes
Writer	ML Aggarwal
Book Name	Understanding
Topics	Solution of Exe-13.3 Questions
Edition	2023-2024

Quadrilaterals Shapes Exe-13.3

ML Aggarwal Class 8 ICSE Maths Solutions

Page-244

Question 1. Identify all the quadrilaterals that have

(i) four sides of equal length
(ii) four right angles.

Answer:

(i) Any quadrilateral whose four sides are equal in length is a square or rhombus.
(ii) A quadrilateral having four right angles is a square or a rectangle.

Question 2. Explain how a square is

(i) a quadrilateral
(ii) a parallelogram
(iii) a rhombus
(iv) a rectangle.

Answer:

(i) A square is a quadrilateral which has four sides and four angles whose sum is 360°.
(ii) A square is a parallelogram whose opposite sides are parallel.
(iii) A square is a parallelogram whose sides are equal and so, it is a rhombus.
(iv) A square is a parallelogram whose each angle is 90°. So, it is a rectangle.

Question 3. Name the quadrilaterals whose diagonals

(i) bisect each other
(ii) are perpendicular bisectors of each other
(iii) are equal.

Answer:

(i) Rectangle, square, rhombus, parallelogram.
(ii) Square, rhombus.
(iii) Square, rectangle.

Question 4. One of the diagonals of a rhombus and its sides are equal. Find the angles of the rhombus.

Answer:

In a rhombus, side and one diagonal are equal.
∴ Angles will be 60° and 120°

Question 5. In the given figure, ABCD is a rhombus, find the values of x, y and z.

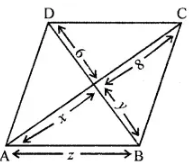
Answer:

In rhombus ABCD.
∵ The diagonals of rhombus bisect each other at right angles.
∴ AO = OC and BO = OD
AO = x, OC = 8 cm, BO =y and OD = 6 cm
∴ x = 8 cm and y = 6 cm

In ∆AOB,
AB² = AO² + BO²
AB² = 8² + 6²
AB² = 64 + 36
AB² = 100 = (10)²
AB = 10 cm

Question 6. In the given figure, ABCD is a trapezium. If ∠A : ∠D = 5 : 7, ∠B = (3x + 11)° and ZC = (5x – 31)°, then find all the angles of the trapezium.

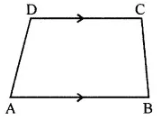
Answer:

ABCD is a trapezium

∠A : ∠D = 5 : 7, ∠B = (3x + 11)^o and ZC = (5x – 31)^o

Then, ∠B + ∠C = 180^o … [because co – interior angle]

(3x + 11)^o + (5x – 31)^o = 180^o

3x + 11 + 5x – 31 = 180^o

8x – 20 = 180^o

8x = 180^o + 20

8x = 200^o

x = 200^o/8

x = 25^o

Then, ∠B = 3x + 11

= (3 × 25) + 11

= 75 + 11

= 86^o

∠C = 5x – 31

= (5 × 25) – 31

= 125 – 31

= 94^o

let us assume the angles ∠A = 5y and ∠D = 7y

sum of co – interior angles are equal to 180^o.

∠A + ∠D = 180^o

5y + 7y = 180^o

12y = 180^o

y = 180^o/12

y = 15^o

Then, ∠A = 5y = (5 × 15) = 75^o

∠D= 7y = (7 × 15) = 105^o

Therefore, the angles are ∠A = 75^o, ∠B = 86^o, ∠C = 94^o and ∠D = 105^o.

Question 7. In the given figure, ABCD is a rectangle. If ∠CEB : ∠ECB = 3 : 2 find

(i) ∠CEB,
(ii) ∠DCF

Answer:

In ∆ BCE, ∠B = 90° (∵ ABCD is a rectangle)
∴ ∠CEB + ∠ECB = 90°
3x + 2x = 90°
⇒ x= 18°
∴ ∠CEB = 3x = 3 × 18° = 54°
Now, ∠CEB = ∠ECD = 54° (Alternate angles)
Also ∠ECD + ∠DCF = 180° (Linear pair)
⇒ ∠DCF = 180 – 54= 126°

Question 8. In the given figure, ABCD is a rectangle and diagonals intersect at O. If ∠AOB = 118°, find

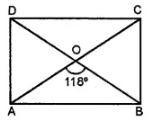
(i) ∠ABO
(ii) ∠ADO
(iii) ∠OCB

Answer:

ABCD is a rectangle and diagonals intersect at O.

∠AOB = 118^o

(i) Consider the ΔAOB,

∠OAB = ∠OBA

Let us assume ∠OAB = ∠OBA = y^o

Sum of measures of interior angles of triangle is equal to 180^o.

∠OAB + ∠OBA + ∠AOB = 180^o

y + y + 118^o = 180^o

2x + 118^o = 180^o

2y = 180^o – 118^o

2y = 62^o

y = 62/2

y = 31^o

So, ∠OAB = ∠OBA = 31^o

Hence, ∠ABO = 31^o

(ii) We know that sum of liner pair angles is equal to 180^o.

∠AOB + ∠AOD = 180^o

118^o + ∠AOD = 180^o

∠AOD = 180^o – 118^o

∠AOD = 62^o

Now consider the ΔAOD,

Let us assume the ∠ADO = ∠DAO = x

∠AOD + ∠ADO + ∠DAO = 180^o

62^o + x + x = 180^o

62^o + 2x = 180^o

2x = 180^o – 62

2x = 118^o

x = 118^o/2

x = 59^o

Hence, ∠ADO = 59^o

(iii) ∠OCB = ∠OAD = 59^o  … [because alternate angles are equal]

Question 9. In the given figure, ABCD is a rhombus and ∠ABD = 50°. Find :

(i) ∠CAB
(ii) ∠BCD
(iii) ∠ADC

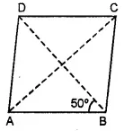
Answer:

(i) We know that diagonals of a rhombus
are ⊥ to each other.

∴ ∠BOA = 90°
In ∆ AOB,
∠OAB + ∠BOA + ∠ABO = 180°
∠OAB + 90° + 50° = 180°
∠OAB = 180 – 140 = 40°
∴ ∠CAB = ∠OAB = 40°

(ii) ∠BCD = 2 ∠ACD = 2 × 40° = 80°
(∵ ∠CAB = ∠ACD alternate angles)
(iii) ∠ADC = 2 ∠BDC = 2 × 50° = 100°
(∵ ∠ABD = ∠BDC alternate angles)

---

Quadrilaterals Shapes Exe-13.3

ML Aggarwal Class 8 ICSE Maths Solutions

Page-245

Question 10. In the given isosceles trapezium ABCD, ∠C = 102°. Find all the remaining angles of the trapezium.

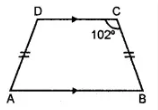
Answer:

AB || CD
∠B + ∠C = 180°
(∵ adjacent angles on the same side of
transversal are supplementary)
⇒ ∠B + 102° = 180°
∠B = 180°- 102° = 78°
As AD = BC (Given)
∴ ∠A = ∠B = 78°
∠A + ∠B + ∠C + ∠D = 360°
78° + 78° + 102° + ∠D = 360°
∠D + 258° = 360°
∠D = 102°

Question 11. In the given figure, PQRS is a kite. Find the values of x and y.

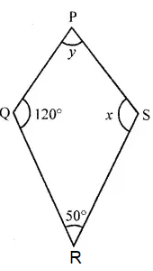
Answer:

In the figure, PQRS is a kite
∠Q = 120° and ∠R = 50°
∴ ∠Q = ∠S
∴ x = 120°
∠P + ∠R = 360° – (120° + 120°)
∠P + ∠R = 360° – 240° = 120°
But ∠R = 50°
∴ ∠P = y = 120°- 50° = 70°
Hence, x = 120°, y = 70°

— End of Quadrilaterals Shapes Exe-13.3 Class 8 ICSE Maths Solutions :–

Return to : – ML Aggarwal Maths Solutions for ICSE Class -8

Thanks