ML Aggarwal Ratio and Proportion Exe-7.2 Class 10 ICSE Maths Solutions

ML Aggarwal Ratio and Proportion Exe-7.2 Class 10 ICSE Maths Solutions . We Provide Step by Step Answer of  Exe-7.2 Questions for Ratio and Proportion as council prescribe guideline for upcoming board exam.  Visit official Website  CISCE  for detail information about ICSE Board Class-10.

ML Aggarwal Ratio and Proportion Exe-7.2 Class 10 ICSE Maths Solutions

Board	ICSE
Subject	Maths
Class	10th
Chapter-7	Ratio and Proportion
Writer / Book	Understanding
Topics	Solutions of Exe-7.2
Academic Session	2024-2025

Ch-7, Ratio and Proportion Exe-7.2

ML Aggarwal Class 10 ICSE Maths Solutions

Question -1 Find the value of x in the following proportions :
(i) 10 : 35 = x : 42
(ii) 3 : x = 24 : 2
(iii) 2.5 : 1.5 = x : 3
(iv) x : 50 :: 3 : 2

Answer -1

(i) 10 : 35 = x : 42
⇒ 35 × x = 10 × 42

x = (10 × 42) / 35

x = 2 × 6,   x = 12

(ii) 3: x = 24: 2

x × 24 = 3 × 2

x = (3 × 2)/ 24

x = ¼

(iii) 2.5: 1.5 = x: 3

1.5 × x = 2.5 × 3

x = (2.5 × 3)/ 1.5

x = 5.0

(iv) x: 50 :: 3: 2

x × 2 = 50 × 3

x = (50 × 3)/ 2

x = 75

Question- 2 Find the fourth proportional to
(i) 3, 12, 15
(ii) 1/3,1/4,1/5
(iii) 1.5, 2.5, 4.5
(iv) 9.6 kg, 7.2 kg, 28.8 kg

Answer -2

(i) Let fourth proportional to
3, 12, 15 be x.
then 3 : 12 :: 15 : x

3 × x = 12 × 15

x = (12 × 15)/ 3

x = 60

(ii) 1/3, 1/4, 1/5

let  x is fourth proportional

1/3: 1/4:: 1/5: x

1/3 × x = 1/4 × 1/5

So we get

x = 1/4 × 1/5 × 3/1

x = 3/20

(iii) 1.5, 2.5, 4.5

let x is fourth proportional

1.5: 2.5 :: 4.5: x

1.5 × x = 2.5 × 4.5

x = (2.5 × 4.5)/ 1.5

x = 7.5

(iv) 9.6 kg, 7.2 kg, 28.8 kg

let x be fourth proportional

9.6: 7.2 :: 28.8: x

9.6 × x = 7.2 × 28.8

x = (7.2 × 28.8)/ 9.6

x = 21.6

Question -3 Find the third proportional to
(i) 5, 10
(ii) 0.24, 0.6
(iii) Rs. 3, Rs. 12
(iv) 21/4 and 7.

Answer -3

(i) Let x be the third proportional to 5, 10,
then 5 : 10 :: 10 : x

5 × x = 10 × 10

x = (10 × 10)/ 5 = 20

the third proportional to 5, 10 is 20.

(ii) let x be third proportional to 0.24, 0.6

0.24: 0.6 :: 0.6: x

0.24 × x = 0.6 × 0.6

x = (0.6 × 0.6)/ 0.24 = 1.5

the third proportional to 0.24, 0.6 is 1.5.

(iii) let x be third proportional to Rs. 3 and Rs. 12

3: 12 :: 12: x

3 × x = 12 × 12

x = (12 × 12)/ 3 = 48

the third proportional to Rs. 3 and Rs. 12 is Rs. 48

(iv) let x as the third proportional to 5 ¼ and 7

5 ¼: 7 :: 7: x

21/4 × x = 7 × 7

x = (7 × 7 × 4)/ 21 = 28/3 = 9 1/3

Question- 4 Find the mean proportion of:

(i) 5 and 80

(ii) 1/12 and 1/75

(iii) 8.1 and 2.5

(iv) (a – b) and (a³ – a²b), a ˃ b

Answer -4

(i) let x as the mean proportion of 5 and 80

5: x :: x: 80

x² = 5 × 80 = 400

x = √400 = 20

so mean proportion of 5 and 80 is 20.

(ii) let x is mean proportion of 1/12 and 1/75

1/12: x :: x: 1/75

x² = 1/12 × 1/75 = 1/900

x = √1/900 = 1/30

So, mean proportion of 1/12 and 1/75 is 1/30.

(iii) let x is mean proportion of 8.1 and 2.5

8.1: x :: x: 2.5

x² = 8.1 × 2.5 = 20.25

x = √20.25 = 4.5

So mean proportion of 8.1 and 2.5 is 4.5.

(iv) let x as the mean proportion of (a – b) and (a³ – a²b), a ˃ b

(a – b): x :: x:(a³ – a²b)

x² = (a – b) (a³ – a²b)

x² = (a – b) a² (a – b)

x² = a² (a – b)²

x = a (a – b)

Hence, mean proportion is a (a – b).

Question -5 If a, 12, 16 and b are in continued proportion find a and b.

Answer- 5 ∵ a, 12, 16, b are in continued proportion, then

a/12 = 12/16 = 16/b

a/12 = 12/16

16a = 144 (By cross multiplication)

a = 144/16 = 9

and 12/16 = 16/b

12b = 16 × 16 = 256 (By cross multiplication)

b = 256/12 = 64/3 = 21 1/3

Hence, a = 9 and b = 64/3 or 21 1/3.

---

Ch-7, Ratio and Proportion Exe-7.2 

ML Aggarwal Class 10 ICSE Maths Solutions

Page-126

Question- 6 What number must be added to each of the numbers 5, 11, 19 and 37 so that they are in proportion ? (2009)

Answer- 6

Let x be added to 5, 11, 19 and 37 to make them in proportion.
5 + x : 11 + x : : 19 + x : 37 + x

(5 + x) (37 + x) = (11 + x) (19 + x)

185 + 5x + 37x + x² = 209 + 11x + 19x + x²

185 + 42x + x² = 209 + 30x + x²

42x – 30x + x² – x² = 209 – 185

12x = 24

x = 2

Question- 7 What number should be subtracted from each of the numbers 23, 30, 57 and 78 so that the remainders are in proportion ? (2004)

Answer- 7

Let x be subtracted from each term, then
23 – x, 30 – x, 57 – x and 78 – x are proportional
23 – x : 30 – x : : 57 – x : 78 – x

(23 – x)/ (30 – x) = (57 – x)/ (78 – x)

(23 – x) (78 – x) = (30 – x) (57 – x)

1794 – 23x – 78x + x² = 1710 – 30x – 57x + x²

x² – 101x + 1794 – x² + 87x – 1710 = 0

– 14x + 84 = 0

14x = 84

x = 84/14 = 6

Question-8 The following numbers, K + 3, K + 2, 3K – 7 and 2K – 3 are in proportion. Find k (2019)

Answer-8

(K + 3) / (K + 2) =  (3K – 7) / (2K – 3 )

⇒ (K + 3) (2K – 3) = (K + 2) (3K – 7).
⇒ 2K² – 3K + 6K – 9 = 3K² – 7K + 6K – 14
⇒ K² – 4K – 5 = 0
⇒ (K – 5) (K + 1) = 0
⇒ K = 5 or K = – 1

Question- 9 If x + 5 is the mean proportion between x + 2 and x + 9, find the value of x.

Answer -9

∵ x + 5 is the mean proportion between x + 2 and x + 9, then
(x + 5)² = (x + 2) (x + 9)
⇒ x² + 10x + 25 = x² + 11x + 18,

and ⇒ x² + 10x – x² – 11x = 18 – 25
so ⇒ – x = – 7
∵ x = 7 Ans.

Question- 10 What number must be added to each of the numbers 16, 26 and 40 so that the resulting numbers may be in continued proportion?

Answer -10

Let x be added to each number then
16 + x, 26 + x and 40 + x
are in continued proportion.

(16 + x)/ (26 + x) = (26 + x)/ (40 + x)

(16 + x) (40 + x) = (26 + x) (26 + x)

640 + 16x + 40x + x² = 676 + 26x + 26x + x²

640 + 56x + x² = 676 + 52x + x²

56x + x² – 52x – x² = 676 – 640

4x = 36

x = 36/4 = 9

Question -11 Find two numbers such that the mean proportional between them is 28 and the third proportional to them is 224.

Answer- 11

Let the two numbers are a and b.
∵ 28 is the mean proportional
∵ a : 28 : : 28 : b

ab = 28² = 784

Here a = 784/b …… (1)

224 is the third proportional

a: b :: b: 224

b² = 224a ….. (2)

substituting the value of a in equation (2)

b² = 224 × 784/b

b³ = 224 × 784

b³ = 175616 = 56³

b = 56

substituting the value of b in equation (1)

a = 784/56 = 14

Hence 14 and 56 are the two numbers.

Question- 12 If b is the mean proportional between a and c, prove that a, c, a² + b², and b² + c² are proportional.

Answer- 12

∵ b is the mean proportional between a and c, then,
b² = a × c ⇒ b² = ac …(i)

a, c, a² + b² and b² + c² are in proportion

a/c = (a² + b²)/ (b² + c²)

a (b² + c²) = c (a² + b²)

Using equation (1)

a (ac + c²) = c (a² + ac)

ac (a + c) = a²c + ac²

Here ac (a + c) = ac (a + c)

Question -13 If b is the mean proportional between a and c, prove that (ab + bc) is the mean proportional between (a² + b²) and (b² + c²).

Answer -13

b is the mean proportional between a and c then
b² = ac …(i)
Now if (ab + bc) is the mean proportional

(ab + bc)² = (a² + b²) (b² + c²)

Consider LHS = (ab + bc)²

on Expanding

= a²b² + b²c² + 2ab²c

equation (1)

= a² (ac) + ac (c)² + 2a. ac. c

= a³c + ac³ + 2a²c²

by Taking ac as common

= ac (a² + c² + 2ac)

= ac (a + c)²

RHS = (a² + b²) (b² + c²)

Using equation (1)

= (a² + ac) (ac + c²)

Taking common

= a (a + c) c (a + c)

= ac (a + c)²

Hence, LHS = RHS

Question -14 If y is mean proportional between x and z, prove that  xyz (x + y + z)³ = (xy + yz + zx)³.

Answer- 14

∵ y is the mean proportional between
x and z, then
y² = xz …(i)

LHS = xyz (x + y + z)³

= xz. y (x + y + z)³

Using equation (1)

= y² y (x + y + z)³

= y³ (x + y + z)³

= [y (x + y + z)]³

= (xy + y² + yz)³

Using equation (1)

= (xy + yz + zx)³

= RHS

Question -15 If a + c = mb and 1/b + 1/d = m/c, prove that a, b, c and d are in proportion.

Answer -15

a + c = mb and 1/b + 1/d = m/c

a + c = mb

Dividing the equation by b

a/b + c/d = m ……. (1)

1/b + 1/d = m/c

Multiplying the equation by c

c/b + c/d = m …… (2)

Using equation (1) and (2)

a/b + c/b = c/b + c/d

So we get

a/b = c/d

Question- 16  If x/a = y/b = z/c, prove that

(i)   x³/a² +y³/b² +z³/c² =(x+y+z)³/(a+b+c)²

(ii)
 

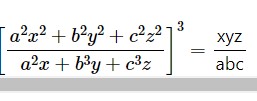
(iii)

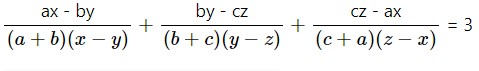
Answer -16

(i) let x/a = y/b = z/c   = k  ∴ x = ak, y = bk, z = ck

(ii)

 

Question- 17 If a/c=c/d=c/f  prove that :

(i) (b² + d² + f²) (a² + c² + e²) = (ab + cd + ef)²

(ii) (a³+c³)² /(b³+d³)² =(e³)² / (f³)²

(iii) a²/b² +c²/d² +e²/f² =ac/bd +ce/df +ae/df

(iv) bdf[(a+b)/b +(c+d)/d +(c+f)/f]³ =27(a+b)(c+d)(e+f)

Answer -17

a/b = c/d = e/f = k

a = bk, c = dk, e = fk

(i) LHS = (b² + d² + f²) (a² + c² + e²)

= (b² + d² + f²) (b²k² + d²k² + f²k²)

Taking out the common terms

= (b² + d² + f²) k² (b² + d² + f²)

= k² (b² + d² + f²)

RHS = (ab + cd + ef)²

= (b. kb + dk. d + fk. f)²

So we get

= (kb² + kd² + kf²)

Taking out common terms

= k² (b² + d² + f²)²

Therefore, LHS = RHS.

(ii)

(iii)

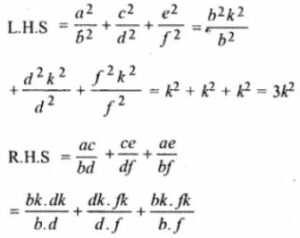
=  k²+ k²+ k²

=3k²

(iv)

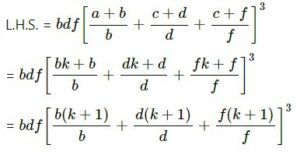
= bdf(k + 1 + k + 1 + k + 1)³
= bdf(3k + 3)³ = 27bdf(k + 1)³
R.H.S. = 27(a + b)(c + d)(e + f)
= 27(bk + b)(dk + d)(fk + f)
= 27b(k + 1)d(k + 1)f(k + 1)
= 27bdf(k + 1)³
∴ L.H.S. = R.H.S.

Question -18 If ax = by = cz; prove that
 x² / yz + y² / zx + z² / xy =bc / a² + ca / b² + ab / c²

Answer -18

Let ax = by = cz = k

x = k/a, y = k/b, z = k/c

Question- 19 If a, b, c and d are in proportion, prove that:
(i) (5a + 7b) (2c – 3d) = (5c + 7d) (2a – 3b)
(ii) (ma + nb) : b = (mc + nd) : d
(iii) (a⁴ + c⁴) : (b⁴ + d⁴) = a² c² : b² d².

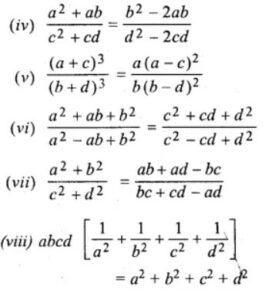
Answer -19 

a, b, c, d are in proportion

Consider a/b = c/d = k

a = b, c = dk

(i) LHS = (5a + 7b) (2c – 3d)

Substituting the values

= (5bk + 7b) (2dk – 3d)

= k (5b + 7b) k (2d – 3d)

= k² (12b) (-d)

= – 12 bd k²

RHS = (5c + 7d) (2a – 3b)

Substituting the values

= (5dk + 7d) (2kb – 3b)

= k (5d + 7d) k (2b – 3b)

= k² (12d) (-b)

= – 12 bd k²

Therefore, LHS = RHS.

Therefore, LHS = RHS.

(iii)( a⁴ + c⁴): (b⁴ + d⁴) = a²c²: b²d²

L.H.S.=  (a⁴ + c⁴)/ (b⁴ + d⁴)

= (k⁴b⁴ + k⁴d⁴) / (b⁴ + d⁴)
= k⁴  (b⁴ + d⁴) / (b⁴ + d⁴)

= k⁴ 
R.H.S. =a²c²/ b²d²
=      k²b^{2 .} k²d² / b²d²

= k⁴ 

Hence L.H.S. = R.H.S.

(iv)

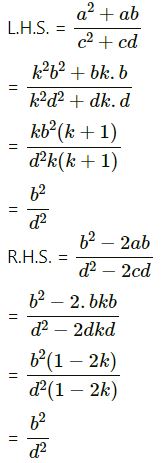
Hence L.H.S. = R.H.S.

(v) ∵ a, b, c, d are in proportion
ab=cd = k(say)
a = bk, c = dk.
L.H.S. = (a+c)³/(b+d)³

= (bk+dk)³ /(b+d)³

= k³(b+d)³ /(b+d)²
= k³
R.H.S. = a(a-c)² /b(b-d)²

= bk(bk-dk)²/  b(b-d)²

= bk.k²(b-d)²/b(b-d)²
= k³
∴ L.H.S. = R.H.S.

(vi)

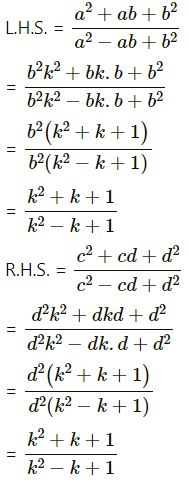
∴ L.H.S. = R.H.S.

(vii)

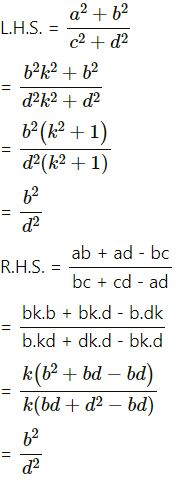
∴ L.H.S. = R.H.S.

(viii)

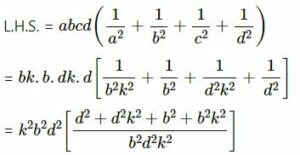
= d²(1 + k²) + b²(1 + k2)
= (1 + k²)(b² + d²)
R.H.S. = a² + b² + c2 + d²
= b²k² + b² + d²k² + d²
= b²(k² + 1) + d²(k² + 1)
= (k² + 1)(b² + d²)
∴ L.H.S. = R.H.S.

---

Ch-7, Ratio and Proportion Exe-7.2 

ML Aggarwal Class 10 ICSE Maths Solutions

Page-127

Question- 20 If x, y, z are in continued proportion, prove that:(x+y)²/(y+z)² =x/z. (2010)

Answer -20

x, y, z are in continued proportion

Let x/y = y/z = k

Then y = kz

x = yk = kz × k

= k²z

Now L.H.S = (x + y)²/(y + z)²

= (k²z + kz)²/(kz + z)²

= {kz(k + 1)}²/{z(k + 1)}²

= {k²z²(k + 1)²}/{z²(k + 1)²}

= k²

R.H.S. = x/z = k²z/z

= k³

∴ L.H.S. = R.H.S.

Question- 21 If a, b, c are in continued proportion, prove that:
(pa² + qab +rb²)/(pb² + qbc + rc²)=a/c

Answer -21

Given a, b, c are in continued proportion (pa² + qab + rb²)/(pb² + qbc + rc²) = a/c

Let a/b = b/c = k

⇒ a = bk and b = ck …(i)

⇒ a = (ck)k = ck² [Using (i)]

and, b = ck

L.H.S = a/c = ck²/c = k²

R.H.S. = {p(ck²)² + q(ck²)ck + r(ck)²}/(p(ck)² + q(ck)c + rc²)

= (pc²k⁴ + qc²k³ + rc²k²)/(pc²k² + qc²k + rc²)

= (c²k²)/c²[(pk² + qk + r)/(pk² + qk + r)]

= k² …(iii)

From (ii) and (iii), L.H.S. = R.H.S

∴ b = ck, a = bk, ckk = ck²

(i) L.H.S = (a + b)/(b + c)

= (a + b)/(b + c)

= (ck² + ck)/(ck + c)

= {ck(k + 1)}/{c(k + 1)}

= k

R.H.S = {a²(b – c)}/{b²(a – b)}

= (ck²)²(ck – c)}/{(ck)²(ck² – ck)}

= {c²k⁴c(k – 1)}/{c²k² ck(k – 1)}

Question- 22 If a, b, c are in continued proportion, prove that:

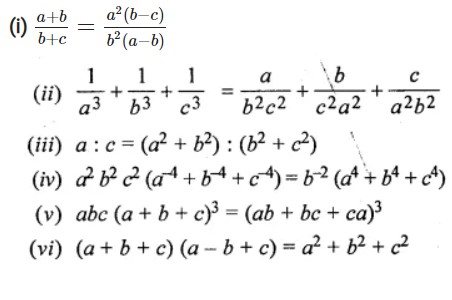
Answer -22

(i) As a, b, c are in continued

Let a/b = b/c = k

= {c³k⁴(k – 1)}/{c³k³(k – 1)}

= k

∴ L.H.S. = R.H.S

(ii) L.H.S = 1/a³ + 1/b³ + 1/c³

= 1/(ck²)³ + 1/(ck)³ + 1/c³

= 1/(c³k⁶) + 1/(c³k³) + 1/c³

= 1/c³[1/k⁶ + 1/k³ + 1/1]

R.H.S = a/(b²c²) + b/(c²a²)+ c/(a²b²)

= (ck²)/(ck²)c² + ck/{(c²(ck²)²} + c/(ck²)² (ck)²

= {ck²/(ck²)c²} + {ck/c²(ck²)²} + {c/(ck²)² (ck)²}

= ck²/(c⁴k²) + ck/(c⁴k⁴) + c/(c⁴k⁶)

= 1/c³ + 1/(c³k³) + 1/(c³k⁶)

= 1/c³[1 + 1/k³ + 1/k⁶]

= 1/c³[1/k⁶ + 1/k³ + 1]

∴ L.H.S. = R.H.S.

(iii) a : c = (a² + b²) : (b² + c²)

⇒ a/c = (a² + b²)/(b² + c²)

L.H.S = a/c = (ck²)/c = k²

R.H.S. = {(ck²)² + (ck)²}/(c²k² + c²)

= (c²k⁴ + c²k²)/(c²k² + c²)

= {c²k²(k² + 1)}/{c²(k² + 1)}

= k²

∴ L.H.S. = R.H.S.

(iv) L.H.S.= a²b²c² (a^-4 + b^-4 + c^-4)

= a²b²c²[1/a⁴ + 1/b⁴ + 1/c⁴]

= (a²b²c²)/a⁴ + (a²b²c²)/b⁴ + (a²b²c²)/c⁴

= (b²c²)/a² + (c²a²)/b² + (a²b²)/c²

= {(ck)^2.c²}/(ck²)² + {c²(ck²)²}/(ck)² + {(ck²)²(ck)²}/c²

= (c²k².c²)/(c²k⁴) + (c².c²k⁴)/(c²k²) + (c²k⁴.c²k²)/c²

= c²/k² + (c²k²)/1 + (c²k⁶)/1

= c²[1/k² + k² + k⁶]

= c²\k²[1 + k⁴ + k⁸]

R.H.S = b^-2[a⁴ + b⁴ + c⁴]

= 1/b²[a⁴ + b⁴ + c⁴]

= 1/(ck)² [(ck²)⁴ + (ck)⁴ + c⁴]

= 1/(c²k²)[c⁴k⁸ + c⁴k⁴ + c⁴]

= c⁴/(c²k²)[k⁸ + k⁴ + 1]

= c²/k² [1 + k⁴ + k⁸]

∴ L.H.S. = R.H.S.

(v) L.H.S. = abc (a + b + c)³

= ck².ck.c[ck² + ck + c]³

= c³k³[c(k² + k + 1)]³

= c²k³.c³.(k² + k + 1)³

= c⁶k³(k² + k + 1)³

R.H.S = (ab + bc + ca)³

= (ck².ck + ck.c + c.ck²)³

= (c²k³ + c²k + c²k²)³

= (c²k³ + c²k² + c²k)³

= [c²k(k² + k + 1)]³

= c⁶k³(k² + k + 1)³

∴ L.H.S. = R.H.S.

(vi) L.H.S. = (a + b + c) (a – b + c)

= (ck² + ck + c)(ck² – ck + c)

= c(k² + k + 1)c(k² – k + 1)

= c²(k² + k + 1)(k² – k + 1)

= c²(k⁴ + k² + 1)

R.H.S = a² + b² + c²

= (ck²)² + (ck)² + (c)²

= c²k⁴ + c²k² + c²

= c²(k⁴ + k² + 1)

∴ L.H.S. = R.H.S.

Question- 23 If a, b, c, d are in continued proportion, prove that:

Answer- 23 a, b, c, d are in continued proportion

∴ a/b = b/c + c/d = k(say)

∴ c = dk, b = ck = dk.k = dk²,

a = bk = dk².k = dk³

(i) L.H.S. = (a³ + b³ + c³) / (b³ + c³ + d³)

= {(dk³)³ + (dk²)³ + (dk)³}/{(dk)²)³ + (dk)³ + d³}

= (d³k⁹ + d³k⁶ + d³k³)/(d³k⁶ + d³k³ + d³)

= {d³k³(k⁶ + k³ + 1)}/{d³(k⁶ + k³ + 1)}

= k³

R.H.S. = a/d = (dk³)/d = k³

∴ L.H.S. = R.H.S.

(ii) L.H.S = (a² – b²)(c² – d²)

= [(dk³)² – (dk²)²][(dk)² – d²]

= (d²k⁶ – d²k⁴)(d²k² – d²)

= d²k⁴(k² – 1)d²(k² – 1)

= d⁴k⁴(k² – 1)²

R.H.S. = (b² – c²)²

= [(dk²)² – (dk)²]²

= [d²k⁴ – d²k²]²

= [d²k²(k² – 1)]²

= d⁴k⁴(k² – 1)1

∴ L.H.S. = R.H.S.

(iii) L.H.S = (a + d)(b + c) – (a + c)(b + d)

= (dk³ + d)(dk² + dk) – (dk³ + dk)(dk² + d)

= d(k³ + 1)dk(k + 1) – dk(k² + 1)d

= d²k(k + 1)(k³ + 1) – d²k(k² + 1)(k² + 1)

= d²k[k⁴ + k³ + k + 1 – k⁴ – 2k² – 1]

= d²k [k³ – 2k² + k]

= d²k² [k² – 2k + 1]

= d²k²(k – 1)²

R.H.S. = (b – c)²

= (dk² – dk)²

= d²k²(k – 1)²

∴ L.H.S. = R.H.S.

(iv) a : d = triplicate ratio of (a – b) : (b – c)

= (a – b)³ : (b – c)³

L.H.S. = a : d = a/d = dk³/d = k³

R.H.S = (a – b)³/(b – c)³

= {(dk³ – dk²)³}/(dk² – dk)³

= d³k⁶(k – 1)³/d³k³(k – 1)³

= k³

∴ L.H.S. = R.H.S.

(v) L.H.S. = {(a – b) / c + (a – c)/b}²  – {(d – b)/c + (d – c)/b}²

= {(dk³ – dk²)/dk} + {(dk³ – dk)/dk²}² – {(d – dk²)/dk + (d – dk)/dk²}²

= {(dk²(k – 1)/dk + dk(k² – 1)/dk²)}² – {d (1 – k²)/dk + d(1 – k)/dk²}²

= {k(k – 1) + (k² – 1)/k}² – {(1 – k²)/k + (1 – k)/k²}²

= {k²(k – 1) + (k² – 1)/k}² – {(k – k² + 1 – k)²}/k²

= {(k³ – k² + k² – 1)/k}² – {(k – k³ + 1 – k)/k²}²

= {(k³ – 1)²}/k² – {(- k³ + 1)²}/k⁴

= {(k³ – 1)²}/k² – {(1 – k³)²}/k⁴

= {(k³ – 1)/k²}² (1 – 1/k²)

= {(k³ – 1)/k²}² {(1 – 1/k²)}

= {(k³ – 1)²(k² – 1)}/k⁴

= {(k³ – 1)²(k² – 1)}/k⁴

= {(k³ – 1)²(k² – 1)}/k⁴

R.H.S. = (a – d)²(1/c² – 1/b²)

= (dk³ – d)² {(1/(d²k²) – 1/(d²k⁴)}

= d²(k³ – 1)² (k² – 1)/(d²k⁴)

= {(k³ – 1)²(k² – 1)}/k⁴

∴ L.H.S. = R.H.S.

—  : End of ML Aggarwal Ratio and Proportion Exe-7.2 Class 10 ICSE Maths Solutions: –

Return to :- ML Aggarwal Solutions for ICSE Class-10

Thanks

Please Share with Your Friends