ML Aggarwal Ratio and Proportion Exe-7.3 Class 10 ICSE Maths Solutions . We Provide Step by Step Answer of Exe-7.3 Questions for Ratio and Proportion as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-10.
ML Aggarwal Ratio and Proportion Exe-7.3 Class 10 ICSE Maths Solutions
| Board | ICSE |
| Subject | Maths |
| Class | 10th |
| Chapter-7 | Ratio and Proportion |
| Writer / Book | Understanding |
| Topics | Solutions of Exe-7.3 |
| Academic Session | 2024-2025 |
Ratio and Proportion Exe-7.3
ML Aggarwal Class 10 ICSE Maths Solutions
Question -1 If a : b : : c : d, prove that
(i) (2a + 5b)/(2a – 5b) = (2c + 5d)/(2c – 5d)
(ii) (5a + 11b)/(5c + 11d) = (5a – 11b)/(5c – 11d)
(iii) (2a + 3b)(2c – 3d) = (2a – 3b)(2c + 3d)
(iv) (la + mb) : (lc + mb) : : (la – mb) : (lc – mb)
Answer- 1
(i) a : b : : c : d
Then a/b = c/d
⇒ 2a/5b = 2c/5d (Multiplying by 2/5)
Applying componendo and dividendo,
(2a + 5b)/(2a – 5b) = (2c + 5d)/(2c – 5d)
(ii) ∵ a : b : : c : d
∴ a/b = c/d
⇒ 5a/11b = 5c/11d (Multiplying by 5/11)
Applying componendo and dividendo,
(5a + 11b)/(5a – 11b) = (5c + 11d)/(5c – 11d)
⇒ (5a + 11b)/(5c + 11d) = (5c + 11b)/(5c – 11d) (Applying alternedo)
(iii) ∵ a : b : : c : d
∴ a/b = c/d ⇒ 2a/3b = 2c/3d (Multiplying by 2/3)
Applying componendo and dividendo,
(2a + 3b)/(2a – 3b) = (2c + 3d)/(2c – 3d)
⇒ (2a + 3b)(2c – 3d)
= (2a – 3b)(2c + 3d) (By cross multiplication)
(iv) ∵ a : b : : c : d
∴ a/b = c/d
⇒ la/mb = lc/md (Multiplying by l/m)
Applying componendo and dividendo,
(la + mb)/(la – mb) = (lc + md)/(lc – md)
⇒ (la + mb)/(lc + md) = (la – mb)/(lc – md) (By alternedo)
⇒ (la + mb) : (lc + md) : : (la – mb) : (lc – md)
Question -2
(ii) if (8a – 5b)/(8c – 5d) = (8a + 5b)/(8c + 5d), prove that a/b=c/d
Answer- 2
(i) (5x + 7y)/(5u + 7v) = (5x – 7y)/(5u – 7v)
Applying alternedo,
(5x + 7y)/(5u + 7y) = (5x – 7y)/(5u – 7v)
Applying componendo and dividendo
⇒ (5x + 7y + 5x – 7y)/(5x + 7y – 5x + 7y) = (5u + 7v + 5u – 7v)/(5u + 7u – 5u + 7v)
⇒ 10x/14y = 10u/14v (Dividing both sides14/10)
⇒ x/y = u/v
Hence proved.
(ii) (8a – 5b)/(8c – 5d) = (8a + 5b)/(8c + 5d)
⇒ (8a + 5b)/(8a – 5b) = (8c + 5d)/(8 – 5d) (using alternedo)
Applying compoundo and dividendo,
(8a + 5b + 8a – 5b)/(8a + 5b – 8a + 5b) = (8c + 5d + 8c – 5c)/(8c + 5d – 8c + 5d)
∴ 16a/10b = 16c/10d
⇒ a/b = c/d (Dividing by 16/10)
Hence, proved.
Question- 3 If (4a + 5b) (4c – 5d) = (4a – 5d) (4c + 5d), prove that a, b, c, d are in proportion.
Answer- 3
(4a + 5b)(4c – 5d) = (4a – 5d)(4c + 5d)
⇒ (4a + 5b)/(4a – 5b) = (4c + 5d)/(4c – 5d)
Applying componendo and dividendo
(4a + 5b + 4a – 5b)/(4a + 5b – 4a + 5b) = (4c + 5d + 4c – 5d)/(4c + 5d – 4c + 5d)
⇒ 8a/10b = 8c/10d
⇒ a/b = c/d
Hence, a, b, c are in proportion.
Question -4 If (pa + qb) : (pc + qd) :: (pa – qb) : (pc – qd) prove that a : b : : c : d
Answer- 4
(pa + qb) : (pc + qd) : : (pa – qb) : (pc – qd)
⇒ (pa + qb)/(pc + qd) = (pa – qb)/(pc – qd)
⇒ (pa + qb)/(pa – qd) = (pc + qd)/(pc – qd)
Applying componendo and dividendo
⇒ (pa + qb + pa – qb)/(pa + qb – pa + qb) = (pc + qd + pc – qd)/(pc – qd – pc + qd)
⇒ (2 pa)/(2 qb) = (2pc)/(2qd)
⇒ a/b = c/d (Dividing by 2p/2q)
Hence a : b : : c = d
Ratio and Proportion Exe-7.3
ML Aggarwal Class 10 ICSE Maths Solutions
Question -5 If (ma + nb): b :: (mc + nd) : d, prove that a, b, c, d are in proportion.
Answer- 5
(ma + nb) : b : : (mc + nd) : d
⇒ (ma + nb)/b = (mc + nd)/d
⇒ mad + nbd = mbc + nbd
⇒ mad = mbc
⇒ ad = bc
⇒ a/b = c/d
Hence a : b : : c : d.
Question -6 If (11a² + 13b²) (11c² – 13d²) = (11a² – 13b²)(11c² + 13d²), prove that a : b :: c : d.
Answer -6
(11a2 + 13b2)(11c2 – 13d2) = (11a2 – 13b2)(11c2 + 13d2)
⇒ (11a2 + 13b2)/(11a2 – 13b2) = (11c2 + 13d2)/(11c2 – 13d2)
Applying componendo and dividendo
(11a2 + 13b2 + 11a2 – 13b2)/(11a2 + 13b2 – 11a2 + 13b2) = (11c2 + 13d2 + 11c2 – 13d2)/(11c2 + 13d2 – 11c2 + 13d2)
⇒ (22a2/26b2) = (22c2/26d2)
⇒ a2/b2 = c2/d2 (Dividing by 22/26)
⇒ a/b = c/d
Hence a : b : : c : d
Question -7 if x=2ab/(a+b )find the value of (x+a) / (x−a) + (x+b)/(x−b)
Answer-7
x = 2ab/(a + b)
⇒ x/a = 2b(a + b)
Applying componendo and dividendo
(x + a)/(x – a)
= (2b + a + b)/(2b – a – b)
= (3b + a)/(b – a) …(i)
Again x/b = 2a/(a + b)
Applying componendo and dividendo,
(x + b)/(x – b)
= (2b + a + b)/(2b – a – b)
= (3b + a)/(b – a) ….(ii)
Adding (i) and (ii)
(x + a)/(x – a) + (x + b)/(x – b)
= (3a + a)/(b – a) + (3a + b)/(a – b)
= -(a + 3b)/(a – b) + (3a + b)/(a – b)
= (- a – 3b + 3a + b)/(a – b)
= (2a – 2b)/(a – b)
= 2(a – b)/(a – b)
= 2
Question-8 if x=8ab/(a+b) find the value of (x+4a)/(x−4a)+(x+4b)/(x−4b)
Answer-8
x = 8ab/(a + b)
⇒ x/4a = 2b/(a + b)
Applying componendo and dividendo,
(x + 4a)/(x – 4a)
= (2b + a + b)/(2b – a – b)
= (3b + a)/(b – a) …(i)
Again,
x/4b = 2a/(a + b)
Applying componendo and dividendo,
(x + 4b)/(x – 4b)
= (2a + a + b)/(2a – a – b)
= (3a + b)/(a – b) …(ii)
Adding (i) and (ii)
(x + 4a)/(x – 4a) + (x + 4b)/(x – 4b)
= (3b + a)/(b – a) + (3a + b)/(a – b)
= -(a + 3b)/(a – b)+ (3a + b)/(a – b)
= -(a – 3b + 3a + b)/(a – b) + (2a – 2b)/(a – b)
= 2(a – b)/(a – b)
= 2
Question-9 If x = (4√6)/(√2 + √3) find the value of( x + 2√2)/(x – 2√2) + (x + 2√3)/(x – 2√3)
Answer -9
x = (4√6)/(√2 + √3)
⇒ x = (4√2 ×√3)/(√2 + √3)
⇒ x/(2√2) = 2√3/(√2 + √3)
Applying componendo and dividendo,
(x + 2√2)/(x – 2√2) = (2√3 + √2 + √3)/(2√3 – √2 – √3)
= (3√3 + √2)/(√3 – √2) …(i)
Again x/(2√3) = (2√2)/(√2 + √3)
Applying componendo and dividendo,
(x + 2√3)/(x – 2√3) = (2√2 + √2 + √3)/(2√2 – √2 – √3)
= (3√2 + √3)/(√2 – √3) …(ii)
Adding (i) and (ii),
(x + 2√2)/(x – 2√2) + (x + 2√3)/(x – 2√3)
= (3√3 + √2)/(√3 – √2) + (3√2 + √3)/( √2 – √3)
= (3√3 + √2)/( √3 – √2) – (3√2 + √3)/(√3 – √2)
= (3√3 + √2 – 3√2 – √3)/( √3 – √2)
= (2√3 – 2√2)/(√3 – √2)
= 2(√3 – √2)/(√3 – √2)
= 2
Question -10 Using properties of proportion ,find x from the following equations
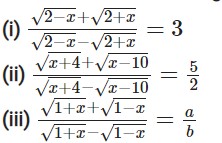
(iv)
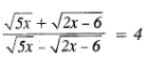
(v)
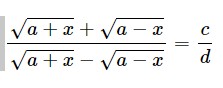
(vi)
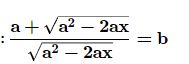
Answer -10



(iv)
(v)

(vi)
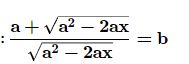
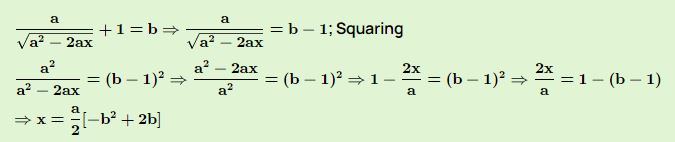
Ratio and Proportion Exe-7.3
ML Aggarwal Class 10 ICSE Maths Solutions
Page-135
Question -11 Using properties of proportion, solve for x. Given that x is positive
(i)
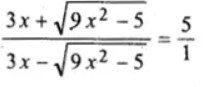
(ii)
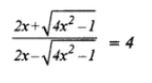
Answer -11
(i)
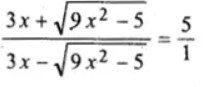

(ii)
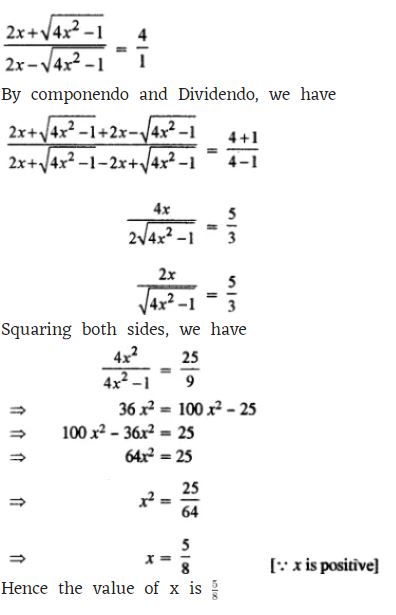
Question-12 Solve (1 + x + x2)/(1 – x + x2) = {62(1 + x)}/{63(1 – x)}
Answer-12
(1 + x + x2)/(1 – x + x2) = {62(1 + x)}/{63(1 – x)}
⇒ (1 – x)(1 + x + x2)/(1 + x)(1 – x + x2) = 62/63
⇒ (1 + x3)/(1 – x3) = 63/62
Applying componendo and dividendo,
(1 + x3 + 1 – x3)/(1 + x3 – 1 + x3) = (63 + 62)/(63 – 62)
⇒ 2/(2x3) = 125/1
⇒ 1/x3 = 125/1
⇒ x3 = 1/125 = (1/5)3
∴ x = 1/5
Question -13 Solve for x : 16{(a – x)/(a + x)}3 = (a + x)/(a – x)
Answer-13
x : 16{(a – x)/(a + x)}3 = (a + x)/(a – x)
⇒ (a + x)/(a – x) × {(a + x)/(a – x)}3 = 16
⇒ {(a + x)/(a – x)}4 = 16(±2)4
⇒ (a + x)/(a – x) = ±2
When (a + x)/(a – x) = 2/1
Applying componendo and dividendo,
(a + x + a – x)/(a + x – a + x) = (2 + 1)/(2 – 1)
⇒ 2a/2x = 3/1
⇒ a/x = 3/1
⇒ 3x = a
∴ x = a/3
When (a + x)/(a – x) = -2/1
Applying componendo and dividendo,
(a + x + a – x)/(a + x – a + x) = (- 2 + 1)/(- 2 – 1)
⇒ 2a/2x = – 1/-3
⇒ a/x = 1/3
⇒ x = 3a
Hence x = a/3, 3a
Question-14 If x = ⌈√(a+1) + √(a-1) ⌉ / ⌈√(a+1) – √(a-1) , using properties of proportion , show that x² – 2ax + 1 = 0 (2012)
Answer-14
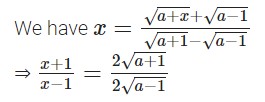
Applying componendo and dividendo,
⇒ (x + 1)2/(x – 1)2 = (a + 1)/(a – 1)
⇒ {(x + 1)2 + (x – 1)2}/{(x + 1)2 – (x – 1)2 = 2a/2
Again applying componendo and dividendo
⇒ (x2 + 1 + 2x + x2 + 1 – 2x)/(x2 + 1 + 2x – x2 – 1 + 2x) = a
⇒ (2x2 + 2)/4x = a
⇒ {2(x2 + 1)}/4x = a
⇒ (x2 + 1)/2x = a
⇒ 2ax = x2 + 1
⇒ x2 – 2ax + 1 = 0
Proved
Question -15 Given x=………… Use componendo and dividendo to prove that ⇒ b2 = 2a2x/(x2 + 1) (2010)
Answer -15

Squaring, both sides we have
⇒ {(x + 1)2}/{(x – 1)2} = (a2 + b2)/(a2 – b2)
⇒(x2 + 1 + 2x)/(x2 + 1 – 2x) = (a2 + b2)/(a2 – b2)
Applying componendo and dividend both sides
⇒ (x2 + 1 + 2x + x2 + 1)/(x2 + 1 + 2x – x2 – 1 + 2x) = (a2 + b2 + a2 – b2)/(a2 + b2 – a2 + b2)
(2x2 + 2)/4x = 2a2/2b2
⇒ (x2 + 1)/2x = a2/b2
⇒ b2 = 2a2x/(x2 + 1)
Ratio and Proportion Exe-7.3
ML Aggarwal Class 10 ICSE Maths Solutions
Question-16 Given that . (a3 + 3ab2)/(b3 + 3a2b) = 63/62 Using componendo and dividendo find a: b. (2009)
Answer -16
Given that (a3 + 3ab2)/(b3 + 3a2b) = 63/62
By componendo and dividendo,
(a3 + 3ab2 + b3 + 3a2b)/(a3 + 3ab2 – b3 – 3a2b) = (63 + 62)/(63 – 62) = 125/1
⇒ {(a + b)3}/{(a – b)3} = (5/1)3
⇒ (a + b)/(a – b) = 5
⇒ a + b = 5a – 5b
⇒ 5a – a – 5b – b = 0
⇒ 4a – 6b = 0
⇒ 4a = 6b
⇒ a/b = 6/4
⇒ a/b = 3/2
a : b = 3 : 2
Question -17 Given (x3 + 12x)/(6x2 + 8) = (y3 + 27y)/(9y2 + 27) Using componendo and dividendo find x : y. (2015)
Answer -17
(x3 + 12x)/(6x2 + 8) = (y3 + 27y)/(9y2 + 27)
Using componendo- dividendo, we have
(x3 + 12x + 6x2 + 8)/(x3 + 12x – 6x2 – 8) = (y3 + 27y + 9y2 + 27)/(y3 + 27y – 9y2 – 27)
⇒ (x + 2)3/(x – 2)3 = (y + 3)3/(9y – 3)3
⇒ {(x + 2)/(x – 1)}3 = {(y + 3)/(y – 3)}3
⇒ (x + 2)/(x – 2) = (y + 3)/(y – 3)
Again using componendo-dividendo, we get
(x + 2 + x – 2)/(x + 2- x + 2) = (y + 3 + y – 3)/(y + 3 – y + 3)
⇒ 2x/4 = 2y/3
⇒ x/2 = y/3
⇒ x/y = 2/3
Thus the required ratio is x : y = 2 : 3
Question-18 Using the properties of proportion, solve the following equation for x; given
(x3 + 3x)/(3x2 + 1) = 341/91
Answer-18
(x3 + 3x)/(3x2 + 1) = 341/91
Applying componendo and dividend
(x3 + 3x + 3x2 + 1)/(x3 + 3x – 3x2 – 1) = (341 + 91)/(341 – 91)
⇒ (x3 + 3x2 + 3x + 1)/(x3 – 3x2 + 3x – 1) = 432/250 = 216/125
⇒ (x + 1)3/(x – 1)3 = 216/125 = (6/5)3
∴ (x + 1)/(x – 1) = 6/5
⇒ 6x – 6 = 5x + 5
⇒ 6x – 5x = 5 + 6
⇒ x = 11
Question-19 If (x + y)/(ax + by) = (y + z)/(ay + bz) = (z + x)/(az + bx) , prove that each of these ratio is equal to 2/(a+b) unless x + y + z = 0
Answer -19
(x + y)/(ax + by) = (y + z)/(ay + bz) = (z + x)/(az + bx)
= (x + y + y + z + z + x)/(ax + by + ay + bz + az + bx)
= {2(x + y + z)}/{x(a + b) + y(a + b) + z(a + b)}
= {2(x + y + z)}/{(a + b)(x + y + z)}
= 2/(a + b) if x + y + z ≠0
Hence proved.
— : End of ML Aggarwal Ratio and Proportion Exe-7.3 Class 10 ICSE Maths Solutions : –
Return to :- ML Aggarwal Solutions for ICSE Class-10
Thanks
Please Share with Your Friends