ML Aggarwal Rational and Irrational Number Chapter Test Class 9 ICSE Maths Solutions

ML Aggarwal Rational and Irrational Number Chapter Test Class 9 ICSE Maths Solutions. We Provide Step by Step Answer of  Chapter Test Questions for Rational and Irrational Number as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-9.

ML Aggarwal Rational and Irrational Number Chapter Test Class 9 ICSE Maths Solutions

Board	ICSE
Subject	Maths
Class	9th
Chapter-1	Rational and Irrational
Topics	Solution of Ch-Test Questions
Edition	2024-2025

 

Rational and Irrational Number Chapter Test

ML Aggarwal Class 9 ICSE Maths Solutions

Question 1. Without actual division, find whether the following rational numbers are terminating decimals or recurring decimals:

(i) 13/45

(ii) -5/56

(iii) 7/125

(iv) -23/80

(v) – 15/66

In case of terminating decimals, write their decimal expansions.

Answer: 

(i)  13/45

We know that

The fraction whose denominator is the multiple of 2 or 5 or both is a terminating decimal

In 13/45

45 = 3 × 3 × 5

Hence, it is not a terminating decimal.

(ii) In -5/56

56 = 2 × 2 × 2 × 7

Hence, it is not a terminating decimal.

(iii) In 7/125

125 = 5 × 5 × 5

We know that

Hence, it is a terminating decimal.

(v) In – 15/66

66 = 2 × 3 × 11

Hence, it is not a terminating decimal.

Question 2. Express the following recurring decimals as vulgar fractions:

Now multiply both sides of equation (1) by 10

10x = 13.4545 ….. (2)

Again multiply both sides of equation (2) by 100

1000x = 1345.4545 …… (3)

By subtracting equation (2) from (3)

990x = 1332

By further calculation

x = 1332/990 = 74/55

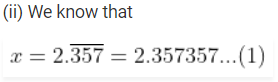
Now multiply both sides of equation (1) by 1000

1000x = 2357.357357 ….. (2)

By subtracting equation (1) from (2)

999x = 2355

By further calculation

x = 2355/999

Question 3. Insert a rational number between 5/9 and 7/13, and arrange in ascending order.

Answer:   A rational number between 5/9 and 7/13

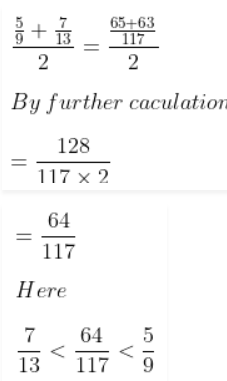
Therefore, in ascending order – 7/13, 64/117, 5/9.

Question 4. Insert four rational numbers between 4/5 and 5/6.

Answer: Rational numbers between 4/5 and 5/6

Here LCM of 5, 6 = 30

So the four rational numbers are

121/150, 122/150, 123/150, 124/150

By further simplification

121/150, 61/75, 41/50, 62/75

Question 5. Prove that the reciprocal of an irrational number is irrational.

Answer:

Consider x as an irrational number

Reciprocal of x is 1/x

If 1/x is a non-zero rational number

Then x × 1/x will also be an irrational number.

We know that the product of a non-zero rational number and irrational number is also irrational.

If x × 1/x = 1 is rational number

Our assumption is wrong

So 1/x is also an irrational number.

Therefore, the reciprocal of an irrational number is also an irrational number.

Question 6. Prove that the following numbers are irrational:

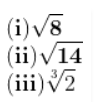
Answer:

(i) √8

If √8 is a rational number

Consider √8 = p/q where p and q are integers

q ˃ 0 and p and q have no common factor

By squaring on both sides

8 = p²/q²

So we get

p² = 8q²

We know that

8p² is divisible by 8

p² is also divisible by 8

p is divisible by 8

Consider p = 8k where k is an integer

By squaring on both sides

p² = (8k)²

p² = 64k²

We know that

64k² is divisible by 8

p² is divisible by 8

p is divisible by 8

Here p and q both are divisible by 8

So our supposition is wrong

Therefore, √8 is an irrational number.

(ii) √14

If √14 is a rational number

Consider √14 = p/q where p and q are integers

q ≠ 0 and p and q have no common factor

By squaring on both sides

14 = p²/q²

So we get

p² = 14q² ….. (1)

We know that

p² is also divisible by 2

p is divisible by 2

Consider p = 2m

Substitute the value of p in equation (1)

(2m)² = 13q²

So we get

4m² = 14q²

2m² = 7q²

We know that

q² is divisible by 2

q is divisible by 2

Here p and q have 2 as the common factor which is not possible

Therefore, √14 is an irrational number.

(iii)

If is a rational number

Consider = p/q where p and q are integers

q ˃ 0 and p and q have no common factor

By cubing on both sides

2 = p³/q³

So we get

p³ = 2q³ ….. (1)

We know that

2q³ is also divisible by 2

p³ is divisible by 2

p is divisible by 2

Consider p = 2k where k is an integer

By cubing both sides

p³ = (2k)³

p³ = 8k³

So we get

2q³ = 8k³

q³ = 4k³

We know that

4k³ is divisible by 2

q³ is divisible by 2

q is divisible by 2

Here p and q are divisible by 2

So our supposition is wrong

Therefore, is an irrational number.

Question 7. Prove that √3 is a rational number. Hence show that 5 – √3 is an irrational number.

Answer:

If √3 is a rational number

Consider √3 = p/q where p and q are integers

q ˃ 0 and p and q have no common factor

By squaring both sides

3 = p²/q²

So we get

P² = 3q²

We know that

3q² is divisible by 3

p² is divisible by 3

p is divisible by 3

Consider p = 3 where k is an integer

By squaring on both sides

P² = 9k²

9k² is divisible by 3

p² is divisible by 3

3q² is divisible by 3

q² is divisible by 3

q is divisible by 3

Here p and q are divisible by 3

So our supposition is wrong

Therefore, √3 is an irrational number.

In 5 – √3

5 is a rational number

√3 is an irrational number (proved)

We know that

Difference of a rational number and irrational number is also an irrational number

So 5 – √3 is an irrational number.

Therefore, it is proved.

Question 8. Prove that the following numbers are irrational:

(i) 3 + √5

(ii) 15 – 2√7

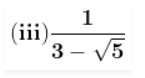
Answer:

(i) If 3 + √5 is a rational number say x

Consider 3 + √5 = x

It can be written as

√5 = x – 3

Here x – 3 is a rational number

√5 is also a rational number.

Consider √5 = p/q where p and q are integers

q ˃ 0 and p and q have no common factor

By squaring both sides

5 = p²/q²

p² = 5q²

We know that

5q² is divisible by 5

p² is divisible by 5

p is divisible 5

Consider p = 5k where k is an integer

By squaring on both sides

p² = 25k²

So we get

5q² = 25k²

q² = 5k²

Here

5k² is divisible by 5

q² is divisible by 5

q is divisible by 5

Here p and q are divisible by 5

So our supposition is wrong

√5 is an irrational number

3 + √5 is also an irrational number.

Therefore, it is proved.

(ii) If 15 – 2√7 is a rational number say x

Consider 15 – 2√7 = x

It can be written as

2√7 = 15 – x

So we get

√7 = (15 – x)/ 2

Here

(15 – x)/ 2 is a rational number

√7 is a rational number

Consider √7 = p/q where p and q are integers

q ˃ 0 and p and q have no common factor

By squaring on both sides

7 = p²/q²

p² = 7q²

Here

7q² is divisible by 7

p² is divisible by 7

p is divisible by 7

Consider p = 7k where k is an integer

By squaring on both sides

p² = 49k²

It can be written as

7q² = 49k²

q² = 7k²

Here

7k² is divisible by 7

q² is divisible by 7

q is divisible by 7

Here p and q are divisible by 7

So our supposition is wrong

√7 is an irrational number

15 – 2√7 is also an irrational number.

Therefore, it is proved.

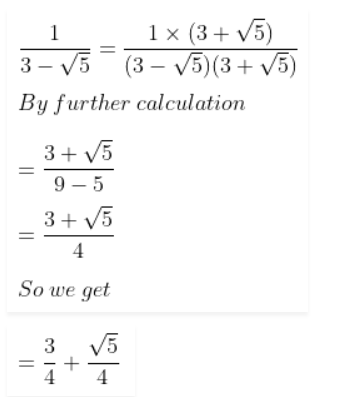
Here

¾ is a rational number and √5/4 is an irrational number

We know that

Sum of a rational and an irrational number is an irrational number.

Therefore, it is proved.

Question 9. Rationalise the denominator of the following:

Question 10. If p, q are rational numbers and p – √15q = 2√3 – √5/4√3 – 3√5, find the values of p and q.

Answer:

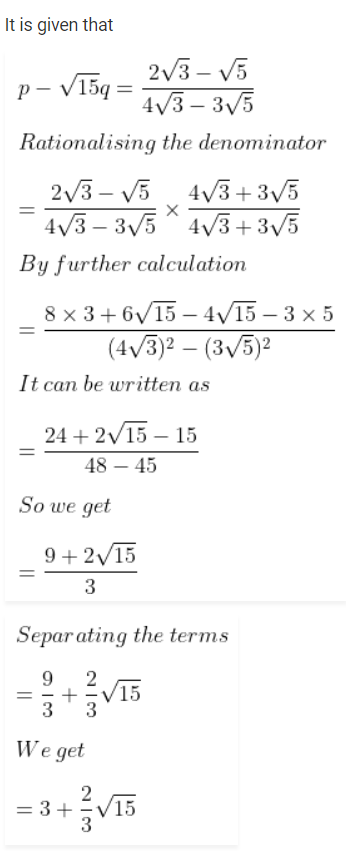
By comparing both sides

p = 3 and q = -2/3

Question 11. If x = 1/3 + 2√2, then find the value of x – 1/x.

Answer:

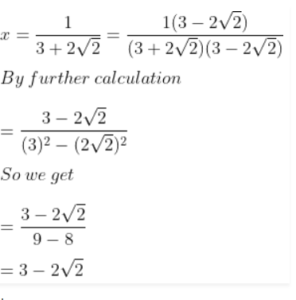
Here

1/x = 3 + 2√2/1 = √3 + 2√2

We know that

x – 1/x = (3 – 2√2) – (3 + 2√2)

By further calculation

= 3 – 2√2 – 3 – 2√2

So we get

= -4√2

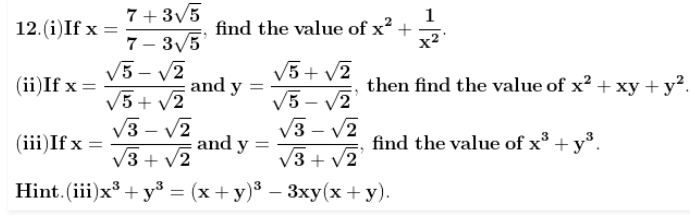
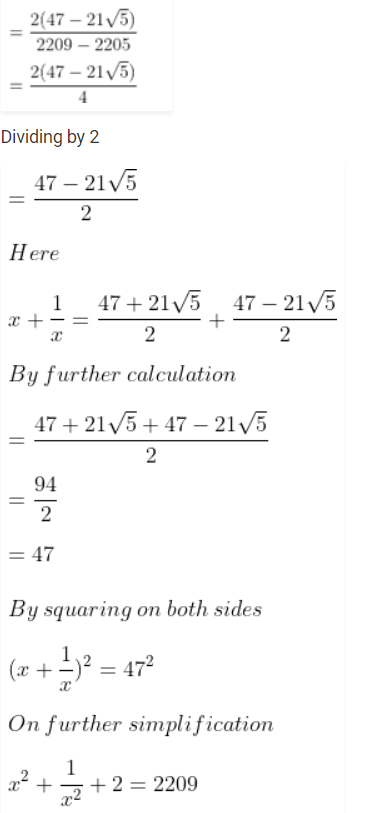
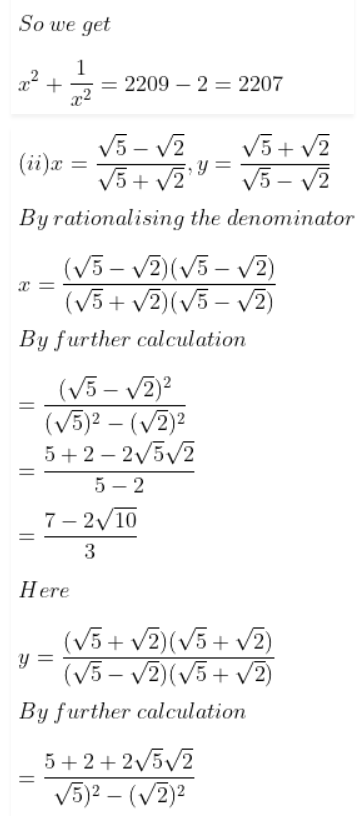
Answer:

We know that

√2 = √2

3.5 = √12.25

√10 = √10

Writing the above numbers in descending order

√18.75, √12.25, √10, √2, – √12.5

So we get

5/2 √3, 3.5, √10, √2, -5/√2

Question 14. Find a rational number and an irrational number between √3 and √5.

Answer:

Let (√3)² = 3 and (√5)² = 5

(i) There exists a rational number 4 which is the perfect square of a rational number 2.

(ii) There can be much more rational numbers which are perfect squares.

(iii) We know that

One irrational number between √3 and √5 = ½ (√3 + √5) = (√3 + √5)/ 2

Question 15. Insert three irrational numbers between 2√3 and 2√5, and arrange in descending order.

Answer:

Take the square

(2√3)² = 12 and (2√5)² = 20

So the number 13, 15, 18 lie between 12 and 20 between (√12)² and (√20)²

√13, √15, √18 lie between 2√3 and 2√5

Therefore, three irrational numbers between

2√3 and 2√5 are √13, √15, √18 or √13, √15 and 3√2.

Here

√20 ˃ √18 ˃ √15 ˃ √13 ˃ √12 or 2√5 ˃ 3√2 ˃ √15 ˃ √13 ˃ 2√3

Therefore, the descending order: 2√5, 3√2, √15, √13 and 2√3.

---

ML Aggarwal Rational and Irrational Number Chapter Test Class 9 ICSE Maths Solutions

Page 39

Question 16. Give an example each of two different irrational numbers, whose

(i) sum is an irrational number.

(ii) product is an irrational number.

Answer:

(i) Consider a = √2 and b = √3 as two irrational numbers

Here

a + b = √2 + √3 is also an irrational number.

(ii) Consider a = √2 and b = √3 as two irrational numbers

Here

ab = √2 √3 = √6 is also an irrational number.

Question 17. Give an example of two different irrational numbers, a and b, where a/b is a rational number.

Answer:

Consider a = 3√2 and b = 5√2 as two different irrational numbers

Here

a/b = 3√2/5√2 = 3/2 is a rational number.

Question 18. If 34.0356 is expressed in the form p/q, where p and q are coprime integers, then what can you say about the factorization of q?

Answer:

We know that

34.0356 = 340356/10000 (in p/q form)

= 85089/2500

Here

85089 and 2500 are coprime integers

So the factorization of q = 2500 = 2²× 5⁴

Is of the form (2^m × 5ⁿ)

Where m and n are positive or non-negative integers.

Question 19. In each case, state whether the following numbers are rational or irrational. If they are rational and expressed in the form p/q, where p and q are coprime integers, then what can you say about the prime factors of q?

(i) 279.034

(iii) 3.010010001…

(iv) 39.546782

(v) 2.3476817681…

(vi) 59.120120012000…

Answer:

(i) 279.034 is a rational number because it has terminating decimals

279.034 = 279034/1000 (in p/q form)

= 139517/500 (Dividing by 2)

We know that

Factors of 500 = 2 × 2 × 5 × 5 × 5 = 2² × 5³

Which is of the form 2^m × 5ⁿ where m and n are positive integers.

It is a rational number as it has recurring or repeating decimals

Consider

x = 76.17893 17893 17893 …..

100000x = 7617893.178931789317893…..

By subtraction

99999x = 7617817

x = 7617817/99999 which is of p/q form

We know that

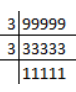
Prime factor of 99999 = 3 × 3 × 11111

q has factors other than 2 or 5 i.e. 3² × 11111

(iii) 3.010010001….

It is neither terminating decimal nor repeating

Therefore, it is an irrational number.

(iv) 39.546782

It is terminating decimal and is a rational number

39.546782 = 39546782/1000000 (in p/q form)

= 19773391/500000

We know that p and q are coprime

Prime factors of q = 2⁵ × 5⁶

Is of the form 2^m × 5ⁿ where m and n are positive integers

(v) 2.3476817681…

Is neither terminating nor repeated decimal

Therefore, it is an irrational number.

(vi) 59.120120012000….

It is neither terminating decimal nor repeated

Therefore, it is an irrational number.

—  : End of ML Aggarwal Rational and Irrational Number Chapter Test Class 9 ICSE Maths Solutions :–

Return to :-  ML Aggarawal Maths Solutions for ICSE  Class-9

Thanks

Please Share with Your Friends