ML Aggarwal Rational and Irrational Number Exe-1.3 Class 9 ICSE Maths Solutions. We Provide Step by Step Answer of Exe-1.3 Questions for Rational and Irrational Number as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-9.
ML Aggarwal Rational and Irrational Number Exe-1.3 Class 9 ICSE Maths Solutions
| Board | ICSE |
| Subject | Maths |
| Class | 9th |
| Chapter-1 | Rational and Irrational |
| Topics | Solution of Exe-1.3 Questions |
| Edition | 2024-2025 |
Rational and Irrational Number Exe-1.3
ML Aggarwal Class 9 ICSE Maths Solutions
Question 1. Locate √10 and √17 on the amber line.
Ans:√10
√10 = √(9 + 1) = √((3)2 + 12)
Now let us construct:
- Draw a line segment AB = 3cm.
- At point A, draw a perpendicular AX and cut off AC = 1cm.
- Join BC.
BC = √10cm

√17
√17 = √(16 + 1) = √((4)2 + 12)
Now let us construct:
- Draw a line segment AB = 4cm.
- At point A, draw a perpendicular AX and cut off AC = 1cm.
- Join BC.
BC = √17cm

Question 2. Write the decimal expansion of each of the following numbers and say what kind of decimal expansion each has:
(i) 36/100
(ii) 4 1/8
(iii) 2/9
(iv) 2/11
(v) 3/13
(vi) 329/400
Ans:
(i) 36/100

36/100 = 0.36
It is a terminating decimal.
(ii) 4 1/8
4 1/8 = (4×8 + 1)/8 = 33/8

33/8 = 4.125
It is a terminating decimal.
(iii) 2/9
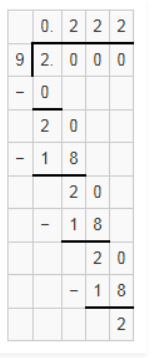
2/9 = 0.222
It is a non-terminating recurring decimal.
(iv) 2/11
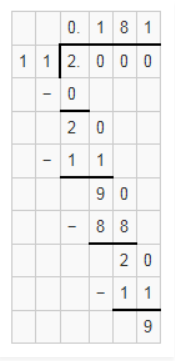
2/11 = 0.181
It is a non-terminating recurring decimal.
(v) 3/13

3/13 = 0.2317692307
It is a non-terminating recurring decimal.
(vi) 329/400
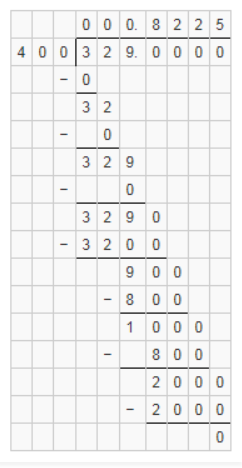
329/400 = 0.8225
It is a terminating decimal.
Question 3. Without actually performing the king division, State whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion:
(i) 13/3125
(ii) 17/8
(iii) 23/75
(iv) 6/15
(v) 1258/625
(vi) 77/210
Ans: We know that, if the denominator of a fraction has only 2 or 5 or both factors, it is a terminating decimal otherwise it is non-terminating repeating decimals.
(i) 13/3125

3125 = 5 × 5 × 5 × 5 × 5
Prime factor of 3125 = 5, 5, 5, 5, 5 [i.e., in the form of 2n, 5n]
It is a terminating decimal.
(ii) 17/8
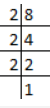
8 = 2 × 2 × 2
Prime factor of 8 = 2, 2, 2 [i.e., in the form of 2n, 5n]
It is a terminating decimal.
(iii) 23/75
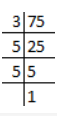
75 = 3 × 5 × 5
Prime factor of 75 = 3, 5, 5
It is a non-terminating repeating decimal.
(iv) 6/15
Let us divide both numerator and denominator by 3
6/15 = (6 ÷ 3) / (15 ÷ 3)
= 2/5
Since the denominator is 5.
It is a terminating decimal.
(v) 1258/625
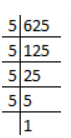
625 = 5 × 5 × 5 × 5
Prime factor of 625 = 5, 5, 5, 5 [i.e., in the form of 2n, 5n]
It is a terminating decimal.
(vi) 77/210
Let us divide both numerator and denominator by 7
77/210 = (77 ÷ 7) / (210 ÷ 7)
= 11/30

30 = 2 × 3 × 5
Prime factor of 30 = 2, 3, 5
It is a non-terminating repeating decimal.
ML Aggarwal Rational and Irrational Number Exe-1.3 Class 9 ICSE Maths Solutions
page 24
Question 4. Without actually performing the long division, find if 987/10500 will have terminating or non-terminating repeating decimal expansion. Give reasons for your answer.
Ans: Given:
The fraction 987/10500
Let us divide numerator and denominator by 21, we get
987/10500 = (987 ÷ 21) / (10500 ÷ 21)
= 47/500
So,
The prime factors for denominator 500 = 2 × 2 × 5 × 5 × 5
Since it is of the form: 2n, 5n
Hence it is a terminating decimal.
Question 5. Write the decimal expansions of the following numbers which have terminating decimal expansions:
(i) 17/8
(ii) 13/3125
(iii) 7/80
(iv) 6/15
(v) 2²×7/54
(vi) 237/1500
Ans:
(i) 17/8

17/8 = 2.125
(ii) 13/3125

13/3125 = 0.00416
(iii) 7/80

7/80 = 0.0875
(iv) 6/15
Let us divide both numerator and denominator by 3, we get
6/15 = (6 ÷ 3) / (15 ÷ 3)
= 2/5
Since the denominator is 5,
It is terminating decimal.
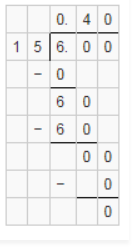
6/15 = 0.4
(v) (2²×7)/54
We know that the denominator is 54
It is a terminating decimal.
(2²×7)/54 = (2 × 2 × 7) / (5 × 5 × 5 × 5)
= 28/625
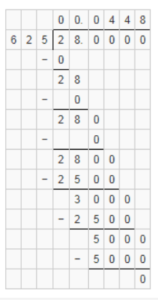
28/625 = 0.0448
It is a terminating decimal.
(vi) 237/1500
Let us divide both numerator and denominator by 3, we get
237/1500 = (237 ÷ 3) / (1500 ÷ 3)
= 79/500
Since the denominator is 500,
Its factors are, 500 = 2 × 2 × 5 × 5 × 5
= 22 × 53
It is terminating decimal.

237/1500= 79/500 = 0.1518
Question 6. Write the denominator of the rational number 257/5000 in the form 2m × 5n where m, n is non-negative integers. Hence, write its decimal expansion on without actual division.
Ans: Given:
The fraction 257/5000
Since the denominator is 5000,
The factors for 5000 are:

5000 = 2 × 2 × 2 × 5 × 5 × 5 × 5
= 23 × 54
257/5000 = 257/(23 × 54)
It is a terminating decimal.
So,
Let us multiply both numerator and denominator by 2, we get
257/5000 = (257 × 2) / (5000 × 2)
= 514/10000
= 0.0514
Question 7. Write the decimal expansion of 1/7. Hence, write the decimal expression of? 2/7, 3/7, 4/7, 5/7 and 6/7.
Ans:
Given:
The fraction: 1/7

1/7 = 0.142857142857
Since it is recurring,

Question 8. Express the following numbers in the form p/q’. Where p and q are both integers and q≠0;

Since there is one repeating digit after the decimal point,
Multiplying by 10 on both sides, we get
10x = 3.3333…
Now, subtract both the values,
9x = 3
x = 3/9
= 1/3
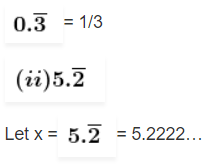
Since there is one repeating digit after the decimal point,
Multiplying by 10 on both sides, we get
10x = 52.2222…
Now, subtract both the values,
9x = 52 – 5
9x = 47
x = 47/9
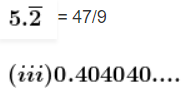
Let x = 0.404040
Since there is two repeating digit after the decimal point,
Multiplying by 100 on both sides, we get
100x = 40.404040…
Now, subtract both the values,
99x = 40
x = 40/99
0.404040… = 40/99
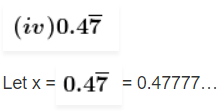
Since there is one non-repeating digit after the decimal point,
Multiplying by 10 on both sides, we get
10x = 4.7777
Since there is one repeating digit after the decimal point,
Multiplying by 10 on both sides, we get
100x = 47.7777
Now, subtract both the values,
90x = 47 – 4
90x = 43
x = 43/90
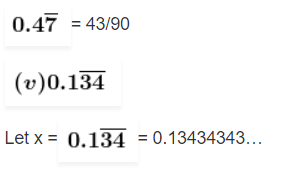
Since there is one non-repeating digit after the decimal point,
Multiplying by 10 on both sides, we get
10x = 1.343434
Since there is two repeating digit after the decimal point,
Multiplying by 100 on both sides, we get
1000x = 134.343434
Now, subtract both the values,
990x = 133
x = 133/990
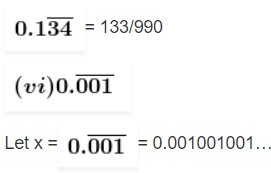
Since there is three repeating digit after the decimal point,
Multiplying by 1000 on both sides, we get
1000x = 1.001001
Now, subtract both the values,
999x = 1
x = 1/999
Question 9. Classify the following numbers as rational or irrational:
(i) √23
(ii) √225
(iii) 0.3796
(iv) 7.478478
(v) 1.101001000100001…
![]()
Ans:
(i) √23
Since, 23 is not a perfect square,
√23 is an irrational number.
(ii) √225
√225 = √(15)2 = 15
Since, 225 is a perfect square,
√225 is a rational number.
(iii) 0.3796
0.3796 = 3796/1000
Since, the decimal expansion is terminating decimal.
0.3796 is a rational number.
(iv) 7.478478
Let x = 7.478478
Since there is three repeating digit after the decimal point,
Multiplying by 1000 on both sides, we get
1000x = 7478.478478…
Now, subtract both the values,
999x = 7478 – 7
999x = 7471
x = 7471/999
7.478478 = 7471/999
Hence, it is neither terminating nor non-terminating or non-repeating decimal.
7.478478 is an irrational number.
(v) 1.101001000100001…
Since number of zero’s between two consecutive ones are increasing. So it is non-terminating or non-repeating decimal.
1.101001000100001… is an irrational number.
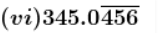
Let x = 345.0456456
Multiplying by 10 on both sides, we get
10x = 3450.456456
Since there is three repeating digit after the decimal point,
Multiplying by 1000 on both sides, we get
1000x = 3450456.456456…
Now, subtract both the values,
10000x – 10x = 3450456 – 345
9990x = 3450111
x = 3450111/9990
Since, it is non-terminating repeating decimal.
Question 10. The following real numbers have decimal expansions as given below. In each case, state whether they are rational or not. If they are rational and expressed in the form p/q, where p, q are integers, q≠ 0 and p, q are co-prime, then what can you say about the prime factors of q?
(i) 37.09158
![]()
(iii) 8.9010010001…
(iv) 2.3476817681…
Ans:
(i) 37.09158
We know that
It has terminating decimal
Here
It is a rational number and factors of q will be 2 or 5 or both.
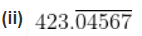
We know that
It has non-terminating recurring decimals
Here
It is a rational number.
(iii) 8.9010010001…
We know that
It has non-terminating, non-recurring decimal.
Here
It is not a rational number.
(iv) 2.3476817681…
We know that
It has non-terminating, recurring decimal.
Here
It is a rational number and the factors of q are prime factors other than 2 and 5.
Question 11. Insert an irrational number between the following.
(i) 1/3 and ½
(ii) -2/5 and ½
(iii) 0 and 0.1
Ans:
(i) One irrational number between 1/3 and ½
½ = 0.5
So there are infinite irrational numbers between 1/3 and ½.
One irrational number among them can be 0.4040040004…
(ii) One irrational number between -2/5 and ½
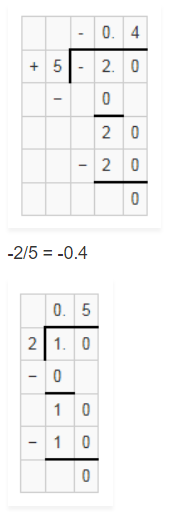
½ = 0.5
So there are infinite irrational numbers between -2/5 and ½.
One irrational number among them can be 0.1010010001…
(iii) One irrational number between 0 and 0.1
There are infinite irrational numbers between 0 and 1.
One irrational number among them can be 0.06006000600006…
Question 12. Insert two irrational numbers between 2 and 3.
Ans: 2 is expressed as √4
And 3 is expressed as √9
So, two irrational numbers between 2 and 3 or √4 and √9 are √5, √6
Question 13. Write two irrational numbers between 4/9 and 7/11.
Ans: 4/9 is expressed as 0.4444…
7/11 is expressed as 0.636363…
So, two irrational numbers between 4/9 and 7/11 are 0.4040040004… and 0.6060060006…
Question 14. Find one rational number between √2 and √3.
Ans: √2 is expressed as 1.4142…
√3 is expressed as 1.7320…
So, one rational number between √2 and √3 is 1.5.
Question 15. Find two rational numbers between 2√3 and √15.
Ans: √12 = √(4×3) = 2√3
Since, 12 < 12.25 < 12.96 < 15
So, √12 < √12.25 < √12.96 < √15
Hence, two rational numbers between √12 and √15are [√12.25, √12.96] or [√3.5, √3.6].
Question 16. Insert irrational numbers between √5 and √7.
Ans: Since, 5 < 6 < 7
So, irrational number between √5 and √7 is √6.
Question 17. Insert two irrational numbers between √3 and √7.
Ans: Since, 3 < 4 < 5 < 6 < 7
So,
√3 < √4 < √5 < √6 < √7
But √4 = 2, which is a rational number.
So,
Two irrational numbers between √3 and √7 are √5 and √6.
— : End of ML Aggarwal Rational and Irrational Number Exe-1.3 Class 9 ICSE Maths Solutions :–
Return to :- ML Aggarawal Maths Solutions for ICSE Class-9
Thanks
Please Share with Your Friends



Thanks icse help