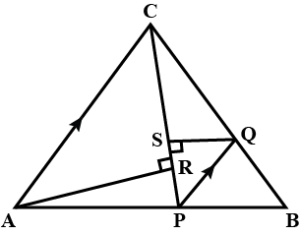ML Aggarwal Similarity Ch-Test Class 10 ICSE Maths Solutions

ML Aggarwal Similarity Ch-Test Class 10 ICSE Maths Solutions Ch-13. We Provide Step by Step Answer of Ch-Test Questions for Similarity as council prescribe guideline for upcoming board exam. Visit official Website  CISCE  for detail information about ICSE Board Class-10.

ML Aggarwal Similarity Ch-Test Class 10 ICSE Maths Solutions Ch-13

Board	ICSE
Subject	Maths
Class	10th
Chapter-13	Similarity
Writer / Book	Understanding
Topics	Solutions of Ch-Test
Academic Session	2024-2025

Ch-13 Similarity Ch-Test

ML Aggarwal Class 10 ICSE Maths Solutions

Page 294

Question 1 In the adjoining figure, ∠1 = ∠2 and ∠3 = ∠4. Show that PT x QR = PR x ST.

Answer 1

Given: In the given figure,
∠1 = ∠1 and ∠3 = ∠4

To prove : PT × QR = PR × ST
Proof: ∠1 = ∠2
Adding ∠6 to both sides
∠1 + ∠6 = ∠2 + ∠6
∠SPT = ∠QPR
In ∆PQR and ∆PST

From above ∠SPT = ∠QPR

∠3 = ∠4

Therefore, ∆PQR ~ ∆PST

So, PT/PR = ST/QR

By cross multiplication we get,

PT x QR = PR x ST

Hence, it is proved that PT x QR = PR x ST

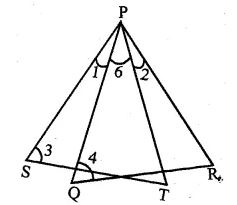
Question 2 In the adjoining figure, AB = AC. If PM ⊥ AB and PN ⊥ AC, show that PM x PC = PN x PB.

Answer 2

Given : In the given figure,
AB = AC, PM ⊥ AB and PN ⊥ AC
To prove : PM × PC = PN × PB
Proof: In ∆ABC, AB = AC
∠B = ∠C
Now in ∆CPN and ∆BPM,

∠N = ∠M … [both angles are equal to 90^o]

∠C = ∠B … [from above]

Therefore, ∆CPN ~ ∆BPM … [from AA axiom]

So, PC/PB = PN/PM

By cross multiplication we get,

PC x PM = PN x PB

Hence, it is proved that, PM x PC = PN x PB

Question 3 

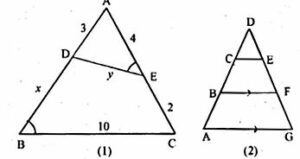
(a) In the figure (1) given below. ∠AED = ∠ABC. Find the values of x and y.

(b) In the fig. (2) given below, CD = 1/2 AC, B is mid-point of AC and E is mid-point of DF. If BF || AG, prove that :
(i) CE || AG
(ii) 3 ED = GD.

Answer 3

(a) Given : In following figure, ∠AED = ∠ABC
Required: The values of x and y.
Now, in ∆ABC and ∆ADE
∠AED = ∠ABC (given)
∠A = ∠A (common)
∴ ∆ABC ~ ∆ADE
(By A.A. axiom of similarity)

Then, AD/AC = DE/BC

3/(4 + 2) = y/10

3/6 = y/10

By cross multiplication we get,

y = (3 x 10)/6

y = 30/6

y = 5

Now, consider AB/AE = BC/DE

(3 + x)/4 = 10/y

(3 + x)/4 = 10/5

By cross multiplication,

5(3 + x) = 10 x 4

15 + 5x = 40

5x = 40 – 15

5x = 25

X = 25/5

x = 5

Hence, the value of x = 5 cm and y = 5 cm

(b) From the question it is given that,

CD = ½ AC

BF || AG

(i) We have to prove that, CE || AG 

Consider, CD = ½ AC

AC = 2BC … [because from the figure B is mid-point of AC]

So, CD = ½ (2BC)

CD = BC

Hence, CE || BF … [equation (i)]

Given, BF || AG … [equation (ii)]

By comparing the results of equation (i) and equation (ii) we get,

CE || AG

(ii) We have to prove that, 3 ED = GD

Consider the ∆AGD,

CE || AG … [above it is proved]

So, ED/GD = DC/AD

AD = AB + BC + DC

= DC + DC + DC

= 3DC

So, ED/GD = DC/(3DC)

ED/GD = 1/(3(1))

ED/GD = 1/3

3ED = GD

Hence,

it is proved that, 3ED = GD

Question 4  In the given figure, P is a point on AB such that PB : AP = 3 : 4 and PQ || AC.

(i) Calculate PQ : AC.

(ii) If AR ⊥ CP, QS ⊥ CB and  QS = 6 cm, calculate the length of AR

Answer 4

(i) Given, AP : PB = 4 : 3.

Since, PQ || AC. Using Basic Proportionality theorem,

Now, ∠PQB = ∠ACB       (Corresponding angles)

∠QPB = ∠CAB                (Corresponding angles)

∴ΔPBQ ~ ΔABC              (AA similarity)

(ii) ∠ARC = ∠QSP = 90°

∠ACR = ∠SPQ             (Alternate angles)

∴∆ARC ~ ∆QSP                     (AA similarity)

Question 5 In a ∆ABC, D and E are points on the sides AB and AC respectively such that DE || BC. If AD = 2.4 cm, AE = 3.2 cm, DE = 2 cm and BC = 5 cm, find BD and CE.

Answer 5

Given : In ∆ABC, D and E are the points
on the sides AB and AC respectively
DE || BC
AD = 2.4 cm, AE = 3.2 cm,
DE = 2 cm, BC = 5 cm

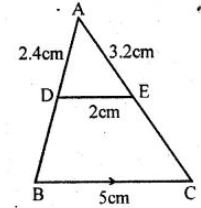
Consider the ∆ABC,

Given, DE || BC

So, AD/AB = AE/AC = DE/BC

Now, consider AD/AB = DE/BC

2.4/AB = 2/5

AB = (2.4 x 5)/2

AB = 12/2

AB = 6 cm

Then, consider AE/AC = DE/BC

3.2/AC = 2/5

AC = (3.2 x 5)/2

AC = 16/2

AC = 8 cm

Hence, BD = AB – AD

= 6 – 2.4

= 3.6 cm

CE = AC – AE

= 8 – 3.2

= 4.8 cm

---

ML Aggarwal Similarity Ch-Test Class 10 ICSE Maths Solutions Ch-13

Page 295

Question 6  In a ∆ABC, D and E are points on the sides AB and AC respectively such that AD = 5.7cm, BD = 9.5cm, AE = 3.3cm and AC = 8.8cm. Is DE || BC? Justify your answer.

Answer 6

In ∆ABC, D and E are points on the sides AB and AC respectively
AD = 5.7 cm, BD = 9.5 cm, AE = 3.3 cm and AC = 8.8 cm

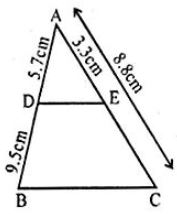
Consider the ∆ABC,

EC = AC – AE

= 8.8 – 3.3

= 5.5 cm

Then, AD/DB = 5.7/9.5

= 57/95

By dividing both numerator and denominator by 19 we get,

= 3/5

AE/EC = 3.3/5.5

= 33/55

By dividing both numerator and denominator by 11 we get,

= 3/5

So, AD/DB = AE/EC

Hence, DE || BC

Question 7 If the areas of two similar triangles are 360 cm² and 250 cm² and if one side of the first triangle is 8 cm, find the length of the corresponding side of the second triangle.

Answer 7

Let ∆ABC and ∆DEF are similar and area of
∆ABC = 360 cm²

let us assume area of ∆PQR = 360 cm², QR = 8 cm

And area of ∆XYZ = 250 cm²

Assume YZ = a

We know that, area of ∆PQR/area of ∆XYZ = QR²/yz²

360/250 = (8)²/a²

360/250 = 64/a²

By cross multiplication we get,

a² = (250 x 64)/360

a² = 400/9

a = √(400/9)

a = 20/3

a =
6 (2/3)

Therefore, the length of the corresponding side of the second triangle YZ =
6 (2/3)

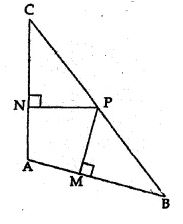
Question 8 In the adjoining figure, D is a point on BC such that ∠ABD = ∠CAD. If AB = 5 cm, AC = 3 cm and AD = 4 cm, find
(i) BC
(ii) DC
(iii) area of ∆ACD : area of ∆BCA.

Answer 8

In ∆ABC and ∆ACD
∠C = ∠C (Common)
∠ABC = ∠CAD (given)
∴ ∆ABC ~ ∆ACD

So, ∆ABC ~ ∆ACD

Then, AB/AD = BC/AC = AC/DC

(i) Consider AB/AD = BC/AC

5/4 = BC/3

BC = (5 x 3)/4

BC = 15/4

BC = 3.75 cm

(ii) Consider AB/AD = AC/DC

5/4 = 3/DC

DC = (3 x 4)/5

DC = 12/5

Dc = 2.4 cm

(iii) Consider the ∆ABC and ∆ACD

∠CAD = ∠ABC … [from the question]

∠ACD = ∠ACB … [common angle for both triangle]

Therefore, ∆ACD ~ ∆ABC

Then, area of ∆ACD/area of ∆ABC = AD²/AB²

= 4²/5²

= 16/25

Hence, area of ∆ACD : area of ∆BCA is 16: 25.

Question 9 In the adjoining figure, the diagonals of a parallelogram intersect at O. OE is drawn parallel to CB to meet AB at E, find area of DAOE : area of ||gm ABCD.

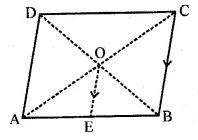
Answer 9

In the figure
Diagonals of parallelogram ABCD are
AC and BD which intersect each other at O.
OE is drawn parallel to CB to meet AB in E.

In the figure four triangles have equal area.

So, area of ∆OAB = ¼ area of parallelogram ABCD

Then, O is midpoint of AC of ∆ABC and DE || CB

E is also midpoint of AB

Therefore, OE is the median of ∆AOB

Area of ∆AOE = ½ area of ∆AOB

= ½ × ¼ area of parallelogram ABCD

= 1/8 area of parallelogram ABCD

So, area of ∆AOE/area of parallelogram ABCD = 1/8

Hence,

area of ∆AOE: area of parallelogram ABCD is 1: 8.

Question 10  In the given figure, ABCD is a trapezium in which AB || DC. If 2AB = 3DC, find the ratio of the areas of ∆AOB and ∆COD.

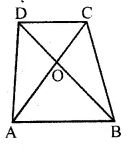
Answer 10

In the given figure, ABCD is trapezium in
which AB || DC, 2AB = 3DC

AB/DC = 3/2

Now, consider ∆AOB and ∆COD

∠AOB = ∠COD … [because vertically opposite angles are equal]

∠OAB = ∠OCD … [because alternate angles are equal]

∆AOB ~ ∆COD … [from AA axiom]

Then, area of ∆AOB/area of ∆COD = AB²/DC²

= 3²/2²

= 9/4

Hence, the ratio of the areas of ∆AOB and ∆COD is 9: 4

---

ML Aggarwal Similarity Ch-Test Class 10 ICSE Maths Solutions Ch-13

Question 11  In the adjoining figure, ABCD is a parallelogram. E is mid-point of BC. DE meets the diagonal AC at O and meet AB (produced) at F. Prove that .

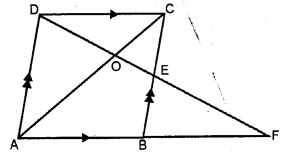
(i) DO : OE = 2 : 1
(ii) area of ∆OEC : area of ∆OAD = 1 : 4.

Answer 11

Given : In || gm ABCD,
E is the midpoint of BC and DE meets the diagonal AC at O
and meet AB produced at F.
To prove : (i) DO : OE = 2 : 1
(ii) area of ∆OEC : area of ∆OAD = 1 : 4
Proof: In ∆AOD and ∆EDC
∠AOD = ∠EOC (vertically opposite angle)
∠OAD = ∠OCB (alt. angles)
∆AOD ~ ∆EOC (AA postulate)

Then, OA/OC = DO/OE = AD/EC = 2EC/EC

OA/OC = DO/OE = 2/1

Hence, OA: OC = 2: 1

(ii) From (i) we proved that, ∆AOD ~ ∆EOC

So, area of ∆OEC/area of ∆AOD = OE²/DO²

area of ∆OEC/area of ∆AOD = 1²/2²

area of ∆OEC/area of ∆AOD = ¼

Hence, area of ∆OEC: area of ∆AOD is 1: 4.

Question 12   A model of a ship is made to a scale of 1 : 250. Calculate :
(i) the length of the ship, if the length of model is 1.6 m.

(ii) the area of the deck of the ship, if the area of the deck of model is 2.4 m².
(iii) the volume of the model, if the volume of the ship is 1 km³.

Answer 12

Scale factor (k) of the model of the ship = 1/250
(i) Length of model = 1.6 m

Then, length of the ship = (1.6 × 250)/1

= 400 m

(ii) Given, the area of the deck of the ship is 2.4 m²

Then, area of deck of the model = 2.4 × (1/250)²

= 1,50,000 m² = 4 m²

(iii) Given, the volume of the model is 1 km³

Then, Volume of ship = (1/250³) × 1 km³

= 1/(250)³ × 1000³

= 4³

= 64 m³

Therefore, volume of ship is 64 m³.

— : End ML Aggarwal Similarity Ch-Test Class 10 ICSE Maths Solutions Ch-13 :–

Return to :- ML Aggarwal Solutions for ICSE Class-10

Thanks

Please Share with Your Friends