ML Aggarwal Similarity Exe-13.3 Class 10 ICSE Maths Solutions

ML Aggarwal Similarity Exe-13.3 Class 10 ICSE Maths Solutions. We Provide Step by Step Answer of Exe-13.3 Questions for Similarity as council prescribe guideline for upcoming board exam. Visit official Website  CISCE  for detail information about ICSE Board Class-10.

ML Aggarwal Similarity Exe-13.3 Class 10 ICSE Maths Solutions

Board	ICSE
Subject	Maths
Class	10th
Chapter-13	Similarity
Writer / Book	Understanding
Topics	Solutions of Exe-13.3
Academic Session	2024-2025

 Similarity Exe-13.3

ML Aggarwal Class 10 ICSE Maths Solutions

Question 1

Given that ∆s ABC and PQR are similar. Find :
(i) The ratio of the area of ∆ABC to the area of ∆PQR if their corresponding sides are in the ratio 1 : 3.
(ii) the ratio of their corresponding sides if area of ∆ABC : area of ∆PQR = 25 : 36.

Answer 1

From the question it is given that,

(i) The area of ∆ABC to the area of ∆PQR if their corresponding sides are in the ratio 1 : 3

Then, ∆ABC ~ ∆PQR

area of ∆ABC/area of ∆PQR = BC²/QR²

BC : QR = 1 : 3

Hence, ∆ABC/area of ∆PQR = 1²/3²

= 1/9

Hence the ratio of the area of ∆ABC to the area of ∆PQR is 1: 9

(ii) The area of ∆ABC to the area of ∆PQR if their corresponding sides are in the ratio 25 : 36

Then, ∆ABC ~ ∆PQR

area of ∆ABC/area of ∆PQR = BC²/QR²

area of ∆ABC/area of ∆PQR = BC²/QR² = 25/36

= (BC/QR)² = (5/6)²

BC/QR = 5/6

Hence the ratio of their corresponding sides is 5 : 6

Question 2

∆ABC ~ DEF. If area of ∆ABC = 9 sq. cm., area of ∆DEF =16 sq. cm and BC = 2.1 cm., find the length of EF.

Answer 2

Let EF = x
Given that
∆ABC ~ ∆DEF,

Area of ∆ABC = 9 sq. cm

Area of ∆DEF =16 sq. cm

area of ∆ABC/area of ∆DEF = BC²/EF²

area of ∆ABC/area of ∆DEF = BC²/EF²

9/16 = BC²/EF²

9/16 = (2.1)²/x²

2.1/x = √9/√16

2.1/x = ¾

By cross multiplication we get,

2.1 × 4 = 3 × x

8.4 = 3x

x = 8.4/3

x = 2.8

Hence, EF = 2.8 cm

Question 3  

∆ABC ~ ∆DEF. If BC = 3 cm, EF = 4 cm and area of ∆ABC = 54 sq. cm. Determine the area of ∆DEF.

Answer 3

∆ABC ~ ∆DEF

BC = 3 cm, EF = 4 cm

Area of ∆ABC = 54 sq. cm.

We know that,

Area of ∆ABC/ area of ∆DEF = BC²/EF²

54/area of ∆DEF = 3²/4²

54/area of ∆DEF = 9/16

By cross multiplication we get,

Area of ∆DEF = (54 × 16)/9

= 6 × 16

= 96 cm

Question 4

The area of two similar triangles are 36 cm² and 25 cm². If an altitude of the first triangle is 2.4 cm, find the corresponding altitude of the other triangle.

Answer 4

The area of two similar triangles are 36 cm² and 25 cm².

Let us assume ∆PQR ~ ∆XYZ, PM and XN are their altitudes.

So, area of ∆PQR = 36 cm²

Area of ∆XYZ = 25 cm²

PM = 2.4 cm

Assume XN = a

area of ∆PQR/area of ∆XYZ = PM²/XN²

36/25 = (2.4)²/a²

By cross multiplication we get,

36a² = 25 (2.4)²

a² = 5.76 × 25/36

a² = 144/36

a² = 4

a = √4

a = 2 cm

Hence, altitude of the other triangle XN = 2 cm.

Question 5

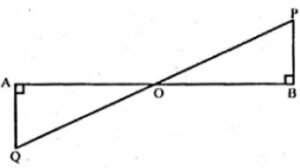
(a) In the figure, (i) given below, PB and QA are perpendiculars to the line segment AB. If PO = 6 cm, QO = 9 cm and the area of ∆POB = 120 cm², find the area of ∆QOA. (2006)

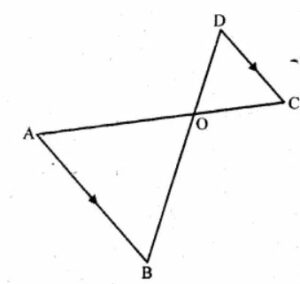
(b) In the figure (ii) given below, AB || DC. AO = 10 cm, OC = 5cm, AB = 6.5 cm and OD = 2.8 cm.
(i) Prove that ∆OAB ~ ∆OCD.
(ii) Find CD and OB.
(iii) Find the ratio of areas of ∆OAB and ∆OCD.

Answer 5

(a) From the question, PO = 6 cm, QO = 9 cm and the area of ∆POB = 120 cm²

Consider the ∆AOQ and ∆BOP,

∠OAQ = ∠OBP … [both angles are equal to 90^o]

∠AOQ = ∠BOP … [because vertically opposite angles are equal]

Hence, ∆AOQ ~ ∆BOP

area of ∆AOQ/area of ∆BOP = OQ²/PO²

Area of ∆AOQ/120 = 9²/6²

Area of ∆AOQ/120 = 81/36

Area of ∆AOQ = (81 × 120)/36

Area of ∆AOQ = 270 cm²

(b) From the question

AB || DC. AO = 10 cm, OC = 5cm, AB = 6.5 cm and OD = 2.8 cm

(i) We have to prove that, ∆OAB ~ ∆OCD

consider the ∆OAB and ∆OCD

∠AOB = ∠COD … [because vertically opposite angles are equal]

∠OBA = ∠OCD … [because alternate angles are equal]

Hence, ∆OAB ~ ∆OCD … [from AAA axiom]

(ii) Consider the ∆OAB and ∆OCD

OA/OC = OB/OD = AB/CD

Now consider OA/OC = OB/OD

10/5 = OB/2.8

OB = (10 × 2.8)/5

OB = 2 × 2.8

OB = 5.6 cm

Then, consider OA/OC = AB/CD

10/5 = 6.5/CD

CD = (6.5 × 5)/10

CD = 32.5/10

CD = 3.25 cm

(iii) We have to find the ratio of areas of ∆OAB and ∆OCD.

From (i) we proved that, ∆OAB ~ ∆OCD

Then, area of (∆OAB)/area of ∆OCD

AB²/CD² = (6.5)²/(3.25)²

= (6.5 × 6.5)/(3.25 × 3.25)

= 2 × 2/1

= 4/1

Hence, the ratio of areas of ∆OAB and ∆OCD = 4: 1.

---

ML Aggarwal Similarity Exe-13.3 Class 10 ICSE Maths Solutions

Page 287

Question 6  

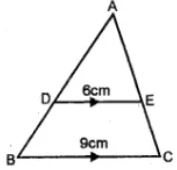
(a) In the figure (i) given below, DE || BC. If DE = 6 cm, BC = 9 cm and area of ∆ADE = 28 sq. cm, find the area of ∆ABC.

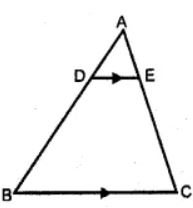
(b) In the figure (iii) given below, DE || BC and AD : DB = 1 : 2, find the ratio of the areas of ∆ADE and trapezium DBCE.

Answer 6

(a) In the figure,
DE || BC
∠D = ∠B and ∠E = ∠C
(Corresponding angles)

Now consider the ∆ADE and ∆ABC,

∠A = ∠A … [common angles for both triangles]

Hence, ∆ADE ~ ∆ABC

Then, area of ∆ADE/area of ∆ABC = (DE)²/(BC)²

28/area of ∆ABC = (6)²/(9)²

28/area of ∆ABC = 36/81

area of ∆ABC = (28 × 81)/36

area of ∆ABC = 2268/36

area of ∆ABC = 63 cm²

(b)

From the question,

DE || BC and AD : DB = 1 : 2,

∠D = ∠B, ∠E = ∠C … [corresponding angles are equal]

Consider the ∆ADE and ∆ABC,

∠A = ∠A … [common angles for both triangles]

Hence, ∆ADE ~ ∆ABC

But, AD/DB = ½

Then, DB/AD = 2/1

Now, adding 1 for both side LHS and RHS,

(DB/AD) + 1 = (2/1) + 1

(DB + AD)/AD = (2 + 1)

Therefore, ∆ADE ~ ∆ABC

Then, area of ∆ADE/area of ∆ABC = AD²/AB²

Area of ∆ADE/area of ∆ABC = (1/3)²

Area of ∆ADE/area of ∆ABC = 1/9

Area of ∆ABC = 9 area of ∆ADE

Area of trapezium DBCE

Area of ∆ABC – area of ∆ADE

9 area of ∆ADE – area of ∆ADE

8 area of ∆ADE

Therefore, area of ∆ADE/area of trapezium = 1/8

Then area of ∆ADE : area of trapezium DBCE = 1: 8

Question 7  In the given figure, DE || BC.
(i) Prove that ∆ADE and ∆ABC are similar.
(ii) Given that AD = 1/2 BD, calculate DE if BC = 4.5 cm.

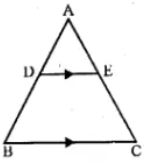
(iii) If area of ∆ABC = 18cm², find the area of trapezium DBCE

Answer 7

(i) From the question it is given that, DE || BC

We have to prove that, ∆ADE and ∆ABC are similar

∠A = ∠A … [common angle for both triangles]

∠ADE = ∠ABC … [because corresponding angles are equal]

Hence, ∆ADE ~ ∆ABC … [AA axiom]

(ii) From (i) we proved that, ∆ADE ~ ∆ABC

Then, AD/AB = AB/AC = DE/BC

So, AD/(AD + BD) = DE/BC

(½ BD)/ ((½BD) + BD) = DE/4.5

(½ BD)/ ((3/2)BD) = DE/4.5

½ × (2/3) = DE/4.5

1/3 = DE/4.5

Hence, DE = 4.5/3

DE = 1.5 cm

(iii) From the question it is given that, area of ∆ABC = 18 cm²

Then, area of ∆ADE/area of ∆ABC = DE²/BC²

area of ∆ADE/18 = (DE/BC)²

area of ∆ADE/18 = (AD/AB)²

area of ∆ADE/18 = (1/3)² = 1/9

area of ∆ADE = 18 × 1/9

area of ∆ADE = 2

area of trapezium DBCE = area of ∆ABC – area of ∆ADE

= 18 – 2

= 16 cm²

Question 8 In the given figure, AB and DE are perpendicular to BC.
(i) Prove that ∆ABC ~ ∆DEC
(ii) If AB = 6 cm: DE = 4 cm and AC = 15 cm, calculate CD.
(iii) Find the ratio of the area of ∆ABC : area of ∆DEC.

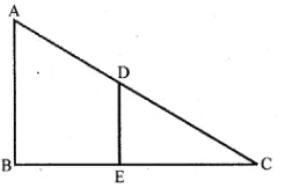
Answer 8

(i) Consider the ∆ABC and ∆DEC,

∠ABC = ∠DEC … [both angles are equal to 90^o]

∠C = ∠C … [common angle for both triangles]

Hence, ∆ABC ~ ∆DEC … [by AA axiom]

(ii) AC/CD = AB/DE

Corresponding sides of similar triangles are proportional

15/CD = 6/4

CD = (15 × 4)/6

CD = 60/6

CD = 10 cm

(iii) area of ∆ABC/area of ∆DEC = AB²/DE²

area of ∆ABC/area of ∆DEC = 6²/4²

area of ∆ABC/area of ∆DEC = 36/16

area of ∆ABC/area of ∆DEC = 9/4

Hence, the ratio of the area of ∆ABC : area of ∆DEC is 9 : 4.

Question 9  In the adjoining figure, ABC is a triangle.
DE is parallel to BC and AD/DB=3/2
(i) Determine the ratios AD/AB,DE/BC
(ii) Prove that ∆DEF is similar to ∆CBF.
Hence, find EF/FB.
(iii) What is the ratio of the areas of ∆DEF and ∆CBF ? (2007)

Answer 9

(i) We have to find the ratios AD/AB, DE/BC,

From the question

AD/DB = 3/2

Then, DB/AD = 2/3

Now add 1 for both LHS and RHS we get,

(DB/AD) + 1 = (2/3) + 1

(DB + AD)/AD = (2 + 3)/3

From the figure (DB + AD) = AB

So, AB/AD = 5/3

Now, consider the ∆ADE and ∆ABC,

∠ADE = ∠B … [corresponding angles are equal]

∠AED = ∠C … [corresponding angles are equal]

Hence, ∆ADE ~ ∆ABC … [by AA similarity]

Then, AD/AB = DE/BC = 3/5

(ii) Now consider the ∆DEF and ∆CBF

∠EDF = ∠BCF … [because alternate angles are equal]

∠DEF = ∠FBC … [because alternate angles are equal]

∠DFE = ∠ABFC … [because vertically opposite angles are equal]

Hence, ∆DEF ~ ∆CBF

So, EF/FB = DE/BC = 3/5

(iii) we have to find the ratio of the areas of ∆DEF and ∆CBF,

We know that, Area of ∆DFE/Area of ∆BFC = DE²/BC²

Area of ∆DFE/Area of ∆BFC = (DE/BC)²

Area of ∆DFE/Area of ∆BFC = (3/5)²

Area of ∆DFE/Area of ∆BFC = 9/25

Hence, the ratio of the areas of ∆DEF and ∆CBF is 9: 25.

---

Page 288

Question 10  

In ∆PQR, MN is parallel to QR and PM/MQ = 2/3

(i) Find MN/QR

(ii) Prove that ∆OMN and ∆PRQ are similar

(iii) Find area  of ∆OMN : area of ∆ORQ

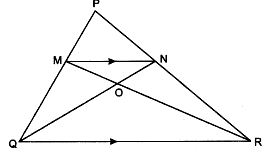
Answer 10

(i) In ΔPMN and ΔPQR, MN || QR

⇒∠PMN=∠PQR   (alternate angles)

⇒∠PNM=∠PRQ  (alternate angles)

=> ΔPMN ~ ΔPQR (AA postulate)

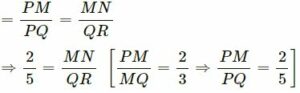
(ii) In ΔOMN and ΔORQ,

∠OMN=∠ORQ   (alternate angles)

∠MNO=∠OQR    (alternate angles)

=> ΔOMN ~ ΔORQ  (AA postulate)

(iii)

---

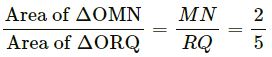
ML Aggarwal Similarity Exe-13.3 Class 10 ICSE Maths Solutions

Question 11

In ∆ABC, AP : PB = 2 : 3. PO is parallel to BC and is extended to Q so that CQ is parallel to BA. Find:
(i) Area ∆APO : area ∆ABC.
(ii) Area ∆APO : area ∆CQO.          (2008)

Answ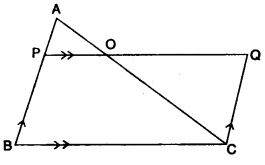er 11 :

Question 12 

(a) In the figure (i) given below, ABCD is a trapezium in which AB || DC and AB = 2 CD. Determine the ratio of the areas of ∆AOB and ∆COD.
(b) In the figure (ii) given below, ABCD is a parallelogram. AM ⊥ DC and AN ⊥ CB. If AM = 6 cm, AN = 10 cm and the area of parallelogram ABCD is 45 cm², find
(i) AB
(ii) BC
(iii) area of ∆ADM : area of ∆ANB.
(c) In the figure (iii) given below, ABCD is a parallelogram. E is a point on AB, CE intersects the diagonal BD at O and EF || BC. If AE : EB = 2 : 3, find
(i) EF : AD
(ii) area of ∆BEF : area of ∆ABD
(iii) area of ∆ABD : area of trap. AFED
(iv) area of ∆FEO : area of ∆OBC.

Answer 12

(a) In trapezium ABCD, AB || DC.
∠OAB = ∠OCD [alternate angles] ∠OBA = ∠ODC
∆AOB ~ ∆COD

So, area of ∆AOB/area of ∆COD = AB²/CD²

= (2CD)²/CD² … [because AB = 2 CD]

= 4CD²/CD²

= 4/1

Hence, the ratio of the areas of ∆AOB and ∆COD is 4: 1.

(b) From the question it is given that,

ABCD is a parallelogram, AM ⊥ DC and AN ⊥ CB

AM = 6 cm

AN = 10 cm

The area of parallelogram ABCD is 45 cm²

Then, area of parallelogram ABCD = DC × AM = BC × AN

45 = DC × 6 = BC × 10

(i) DC = 45/6

Divide both numerator and denominator by 3 we get,

= 15/2

= 7.5 cm

Hence, AB = DC = 7.5 cm

(ii) BC × 10 = 45

BC = 45/10

BC = 4.5 cm

(iii) Now, consider ∆ADM and ∆ABN

∠D = ∠B … [because opposite angles of a parallelogram]

∠M = ∠N … [both angles are equal to 90^o]

Hence, ∆ADM ~ ∆ABN

Therefore, area of ∆ADM/area of ∆ABN = AD²/AB²

= BC²/AB²

= 4.5²/7.5²

= 20.25/56.25

= 2025/5625

= 81/225

= 9/25

Hence, area of ∆ADM : area of ∆ANB is 9: 25

(c) From the question it is given that, ABCD is a parallelogram.

E is a point on AB, CE intersects the diagonal BD at O.

AE : EB = 2 : 3

(i) find EF : AD

So, AB/BE = AD/EF

EF/AD = BE/AB

AE/EB = 2/3 … [given]

Now add 1 to both LHS and RHS we get,

(AE/EB) + 1 = (2/3) + 1

(AE + EB)/EB = (2 + 3)/3

AB/EB = 5/3

EB/AB = 3/5

EF : AD is 3: 5

(ii) we have to find area of ∆BEF: area of ∆ABD,

Then, area of ∆BEF/area of ∆ABD = (EF)²/(AD)²

area of ∆BEF/area of ∆ABD = 3²/5²

= 9/25

area of ∆BEF: area of ∆ABD is 9: 25

(iii) From (ii) area of ∆ABD/area of ∆BEF = 25/9

25 area of ∆BEF = 9 area of ∆ABD

25(area of ∆ABD – area of trapezium AEFD) = 9 area of ∆ABD

25 area of ∆ABD – 25 area of trapezium AEFD = 9 area of ∆ABD

25 area of trapezium AEFD = 25 area of ∆ABD – 9 area of ∆ABD

25 area of trapezium AEFD = 16 area of ∆ABD

area of ∆ABD/area of trapezium AEFD = 25/16

Therefore, area of ∆ABD : area of trapezium AFED = 25: 16

(iv) Now we have to find area of ∆FEO : area of ∆OBC

consider ∆FEO and ∆OBC,

∠EOF = ∠BOC … [because vertically opposite angles are equal]

∠F = ∠OBC … [because alternate angles are equal]

∆FEO ~ ∆OBC

Then, area of FEO/area of ∆OBC = EF²/BC²

EF²/AD² = 9/25

Hence, area of ∆FEO: area of ∆OBC = 9: 25.

Question 13   In the adjoining figure, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1 : 2 and DP produced meets AB produced at Q. If area of ∆CPQ = 20 cm², find

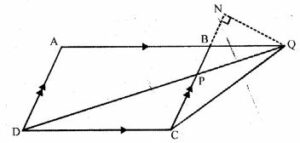
(i) area of ∆BPQ.
(ii) area ∆CDP.
(iii) area of || gm ABCD.

Answer 13

In the figure, ABCD is a parallelogram.
P is a point on BC such that BP : PC = 1 : 2
and DP is produced to meet ABC produced at Q.
Area ∆CPQ = 20 cm²

Then, area of ∆BPQ/area of ∆CPQ = ((½BP) × QN)/((½PC) × QN)

= BP/PC = ½

(i) So, area ∆BPQ = ½ area of ∆CPQ

= ½ × 20

area of ∆BPQ = 10 cm²

(ii) Now we have to find area of ∆CDP,

Consider the ∆CDP and ∆BQP,

Then, ∠CPD = ∠QPD … [because vertically opposite angles are equal]

∠PDC = ∠PQB … [because alternate angles are equal]

∆CDP ~ ∆BQP … [AA axiom]

area of ∆CDP/area of ∆BQP = PC²/BP²

area of ∆CDP/area of ∆BQP = 2²/1²

area of ∆CDP/area of ∆BQP = 4/1

area of ∆CDP = 4 × area ∆BQP

area of ∆CDP = 4 × 10

= 40 cm²

(iii) We have to find the area of parallelogram ABCD,

Area of parallelogram ABCD = 2 area of ∆DCQ

= 2 area (∆DCP + ∆CPQ)

= 2 (40 + 20) cm²

= 2 × 60 cm²

= 120 cm²

Hence, the area of parallelogram ABCD is 120 cm².

---

Similarity Exe-13.3

ML Aggarwal  Class 10 ICSE Maths Solutions

Page 289

Question 14

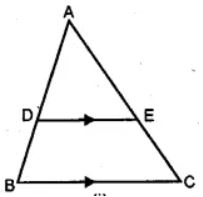
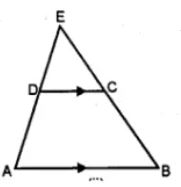
(a) In the figure (i) given below, DE || BC and the ratio of the areas of ∆ADE and trapezium DBCE is 4 : 5. Find the ratio of DE : BC.

(b) In the figure (ii) given below, AB || DC and AB = 2 DC. If AD = 3 cm, BC = 4 cm and AD, BC produced meet at E, find (i) ED (ii) BE (iii) area of ∆EDC : area of trapezium ABCD.

Answer 14

(a) In ∆ABC, DE || BC
Now in ∆ABC and ∆ADE
∠A = ∠A (common)
∠D = ∠B and ∠E = ∠C
(Corresponding angles)
∆ADE ~ ∆ABC

So, area of ∆ADE/area of ∆ABC = (DE)²/(BC)² … [equation (i)]

Then, area of ∆ADE/area of trapezium DBCE = 4/5

area of trapezium DBCE/area of ∆ADE = 5/4

Add 1 for both LHS and RHS we get,

(area of trapezium DBCE/area of ∆ADE) + 1 = (5/4) + 1

(area of trapezium DBCE + area of ∆ADE)/area of ∆ADE = (5 + 4)/4

area of ∆ABC/area of ∆ADE = 9/4

area of ∆ADE/area of ∆ABC = 4/9

From equation (i),

area of ∆ADE/area of ∆ABC = (DE)²/(BC)²

area of ∆ADE/area of ∆ABC = (DE)²/(BC)² = 4²/9²

area of ∆ADE/area of ∆ABC = (DE)²/(BC)² = 2/3

Hence, DE: BC = 2: 3

(b) AB || DC

AB = 2 DC, AD = 3 cm, BC = 4 cm

Now consider ∆EAB,

EA/DA = EB/CB = AB/DC = 2DC/DC = 2/1

(i) EA = 2, DA = 2 × 3 = 6 cm

Then, ED = EA – DA

= 6 – 3

= 3 cm

(ii) EB/CB = 2/1

EB = 2 CB

EB = 2 × 4

EB = 8 cm

(iii) Now, consider the ∆EAB, DC || AB

So, ∆EDC ~ ∆EAB

Therefore, area of ∆EDC/area of ∆ABE = DC²/AB²

area of ∆EDC/area of ∆ABE = DC²/(2DC)²

area of ∆EDC/area of ∆ABE = DC²/4DC²

area of ∆EDC/area of ∆ABE = ¼

Therefore, area of ABE = 4 area of ∆EDC

Then, area of ∆EDC + area of trapezium ABCD = 4 area of ∆EDC

Area of trapezium ABCD = 3 area of ∆EDC

So, area of ∆EDC/area of trapezium ABCD = 1/3

Hence, area of ∆EDC: area of trapezium ABCD = 1: 3

Question 15

(a) In the figure given below, ABCD is a trapezium in which DC is parallel to AB. If AB = 9 cm, DC = 6 cm and BB = 12 cm., find
(i) BP
(ii) the ratio of areas of ∆APB and ∆DPC.

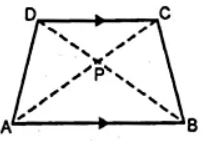
(b) In the figure given below, ∠ABC = ∠DAC and AB = 8 cm, AC = 4 cm, AD = 5 cm.
(i) Prove that ∆ACD is similar to ∆BCA
(ii) Find BC and CD
(iii) Find the area of ∆ACD : area of ∆ABC.

Answer 15

(a) In trapezium ABCD, DC || AB

AB = 9 cm, DC = 6 cm and BB = 12 cm

(i) Consider the ∆APB and ∆CPD

∠APB = ∠CPD … [because vertically opposite angles are equal]

∠PAB = ∠PCD … [because alternate angles are equal]

So, ∆APB ~ ∆CPD

Then, BP/PD = AB/CD

BP/(12 – BP) = 9/6

6BP = 108 – 9BP

6BP + 9BP = 108

15BP = 108

BP = 108/15

BP = 7.2 cm

(ii) area of ∆APB/area of ∆CPD = AB²/CD²

area of ∆APB/area of ∆CPD = 9²/6²

area of ∆APB/area of ∆CPD = 81/36

By dividing both numerator and denominator by 9, we get,

area of ∆APB/area of ∆CPD = 9/4

Hence, the ratio of areas of ∆APB and ∆DPC is 9: 4

(b)  From the question it is given that,

∠ABC = ∠DAC

AB = 8 cm, AC = 4 cm, AD = 5 cm

(i) Now, consider ∆ACD and ∆BCA

∠C = ∠C … [common angle for both triangles]

∠ABC = ∠CAD … [from the question]

So, ∆ACD ~ ∆BCA … [by AA axiom]

(ii) AC/BC = CD/CA = AD/AB

Consider AC/BC = AD/AB

4/BC = 5/8

BC = (4 × 8)/5

BC = 32/5

BC = 6.4 cm

consider CD/CA = AD/AB

CD/4 = 5/8

CD = (4 × 5)/8

CD = 20/8

CD = 2.5 cm

(iii) from (i) we proved that, ∆ACD ~ ∆BCA

area of ∆ACB/area of ∆BCA = AC²/AB²

= 4²/8²

= 16/64

By dividing both numerator and denominator by 16, we get,

= ¼

Hence, the area of ∆ACD : area of ∆ABC is 1: 4.

Question 16 

(a) In the given figure, ∠PQR = ∠PST = 90°, PQ = 5 cm and PS = 2 cm.
(i) Prove that △PQR ∼ APST.
(ii) Find Area of △PQR : Area of quadrilateral SRQT.

Answer 16

Question 17 ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that:
(i) ∆ADE ~ ∆ACB.
(ii) If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
(iii) Find, area of ∆ADE : area of quadrilateral BCED.

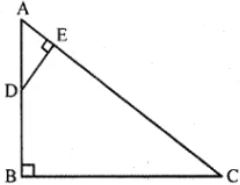
Answer 17

(i) Consider DADE and DACB
∠A = ∠A (Common)
m ∠B = m ∠E = 90°
Thus by angle-angle similarity, triangles,
∆ACB ~ ∆ADE
(ii) Consider ∆ADE and ∆ACB
Since they are similar triangles,

So, AE/AB = AD/AC = DE/BC … [equation (i)]

Consider the ∆ABC, is a right angle triangle

AC² = AB² + BC²

13² = AB² + 5²

169 = AB² + 25

AB² = 169 – 25

AB² = 144

AB = √144

AB = 12 cm

Consider the equation (i),

AE/AB = AD/AC = DE/BC

Take, AE/AB = AD/AC

4/12 = AD/13

1/3 = AD/13

(1 × 13)/3 = AD

AD = 4.33 cm

Now, take AE/AB = DE/BC

4/12 = DE/5

1/3 = DE/5

DE = (5 × 1)/3

DE = 5/3

DE = 1.67 cm

(iii) Now, we have to find area of ∆ADE : area of quadrilateral BCED,

Area of ∆ADE = ½ × AE × DE

= ½ × 4 × (5/3)

= 10/3 cm²

Then, area of quadrilateral BCED = area of ∆ABC – area of ∆ADE

= ½ × BC × AB – 10/3

= ½ × 5 × 12 – 10/3

= 1 × 5 × 6 – 10/3

= 30 – 10/3

= (90 – 10)/3

= 80/3 cm²

So, the ratio of area of ∆ADE : area of quadrilateral BCED = (10/3)/(80/3)

= (10/3) × (3/80)

= (10 × 3)/(3 × 80)

= (1 × 1)/(1 × 8)

= 1/8

Hence, area of ∆ADE : area of quadrilateral BCED is 1: 8.

---

ML Aggarwal  Class 10 ICSE Maths Solutions

Similarity Exe-13.3

Page 289

Question 18   Two isosceles triangles have equal vertical angles and their areas are in the ratio 7 : 16. Find the ratio of their corresponding height.

Answer 18

In two isosceles ∆s ABC and DEF

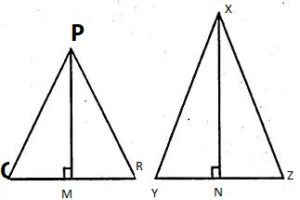
∠P = ∠X … [from the question]

So, ∠Q + ∠R = ∠Y + ∠Z

∠Q = ∠R and ∠Y = ∠Z [because opposite angles of equal sides]

Hence, ∠Q = ∠Y and ∠R = ∠Z

∆PQR ~ ∆XYZ

Then, area of ∆PQR/area of ∆XYZ = PM²/XN² … [from corollary of theorem]

PM²/XN² = 7/16

PM/XN = √7/√16

PM/XN = √7/4

ratio of PM: DM = √7: 4

Question 19   On a map drawn to a scale of 1 : 250000, a triangular plot of land has the following measurements :
AB = 3 cm, BC = 4 cm and ∠ABC = 90°. Calculate
(i) the actual length of AB in km.
(ii) the area of the plot in sq. km:

Answer 19

Scale factor k = 1 : 250000 = 1/250000
Length on map,
AB = 3 cm, BC = 4 cm

(i) We have to find the actual length of AB in km.

Let us assume scale factor K = 1: 250000

K = 1/250000

Then, length of AB of actual plot = 1/k × length of AB on the map

= (1/(1/250000)) × 3

= 250000 × 3

To covert cm into km divide by 100000

= (250000 × 3)/(100 × 1000)

= 15/2

length of AB of actual plot = 7.5 km

(ii) We have to find the area of the plot in sq. km

Area of plot on the map = ½ × AB × BC

= ½ × 3 × 4

= ½ × 12

= 1 × 6

= 6 cm²

Then, area of actual plot = 1/k² × 6 cm²

= 250000² × 6

To covert cm into km divide by (100000)²

= (250000 × 250000 × 6)/(100000 × 100000)

= (25/4) × 6

= 75/2

= 37.5 km²

Question 20 On a map drawn to a scale of 1 : 50,000, a rectangular plot of land ABCD has the following dimensions AB = 6 cm; BC = 8 cm and all angles are right angles. Find :
(i) the actual length of the diagonal distance AC of the plot in km.
(ii) the actual area of the plot in sq. km.

Answer 20

Scale used on the map is 1 : 50,000
Dimensions of a rectangular plot ABCD are AB = 6 cm, BC = 8 cm Since each angle is right angle
∴ By using Pythagoras theorem, we have

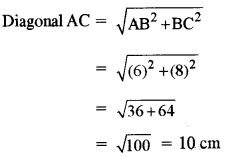
(i) Actual length of the diagonal AC = 10 × 50000 cm
= (500000/100000) km
= 5 km
(ii) Area of the rectangular field ABCD on map
= 6 × 8 = 48 cm²
Actual area of the field = 48 × 500000 × 500000
= 12(10)¹⁰ sq. cm.
= 12 sq. km.

Question 21  A map of a square plot of land is drawn to a scale 1 : 25000. If the area of the plot in the map is 72  cm², find:

(i) the actual area of the plot of the land

(ii) the length of the diagonal in the actual plot of land

Answer 21

Question 22 The model of a building is constructed with the scale factor 1 : 30.
(i) If the height of the model is 80 cm, find the actual height of the building in metres.
(ii) If the actual volume of a tank at the top of the building is 27 m³, find the volume of the tank on the top of the model. (2009)

Answer 22

The model of a building is constructed with the scale factor 1 : 30

So, Height of the model/Height of actual building = 1/30

(i) Given, the height of the model is 80 cm

Then, 80/H = 1/30

H = (80 × 30)

H = 2400 cm

H = 2400/100

H = 24 m

(ii) the actual volume of a tank at the top of the building is 27 m³

Volume of model/Volume of tank = (1/30)³

V/27 = 1/27000

V = 27/27000

V = 1/1000 m³

Hence, Volume of model = 1000 cm³

Question 23   A model of a ship is made to a scale of 1 : 200.
(i) If the length of the model is 4 m, find the length of the ship.
(ii) If the area of the deck of the ship is 160000 m², find the area of the deck of the model.
(iii) If the volume of the model is 200 litres, find the volume of the ship in m³.
(100 litres = m³)

Answer 23

Scale = 1 : 200
(i) Length of a model of ship = 4 m

Then, length of the ship = (4 × 200)/1

= 800 m

(ii) Given, the area of the deck of the ship is 160000 m²

Then, area of deck of the model = 160000 × (1/200)²

= 160000 × (1/40000)

= 4 m²

(iii) Given, the volume of the model is 200 liters

Then, Volume of ship = 200 × (200/1)³

= 200 × 8000000

= (200 × 8000000)/100

= 1600000 m³

—  : End of ML Aggarwal Similarity Exe-13.3 Class 10 ICSE Maths Solutions : –

Return to :- ML Aggarwal Solutions for ICSE Class-10

Thanks

Please Share with Your Friends