ML Aggarwal Solutions Linear Inequations Chapter-Test ICSE Class 10 Ch-4. Understanding APC Maths is a popular publication among ICSE Student. Therefore Step by Step Solved Questions of Chapter Test Inequality is given.

These Solutions are given as council Latest prescibe guideline for board exam. Visit official Website CISCE for detail information about ICSE Board Class-10.
ML Aggarwal Solutions Linear Inequations Chapter-Test ICSE Class 10 Ch-4
| Board | ICSE |
| Subject | Maths |
| Class | 9th |
| Chapter-4 | Linear Inequations |
| Writer / Book | Understanding |
| Topics | Solutions of Chapter-Test |
| Academic Session | 2024-2025 |
Chapter-Test
ML Aggarwal Solutions Linear Inequations ICSE Class 10 Ch-4
Question -1 Solve the inequation : 5x – 2 ≤ 3(3 – x) where x ∈ { – 2, – 1, 0, 1, 2, 3, 4}. Also represent its solution on the number line.
Answer- 1
5x – 2 < 3(3 – x)
⇒ 5x – 2 ≤ 9 – 3x
⇒ 5x + 3x ≤ 9 + 2
or 8x ≤ 11
⇒ x ≤ 11/8
∵ x ∈ {-2, – 1, 0, 1, 2, 3, 4}
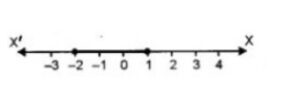
∴ So Solution set = {- 2, – 1, 0, 1}
and Solution set on number line
Question- 2 Solve the inequations : 6x – 5 < 3x + 4, x ∈ I.
Answer- 2
6x – 5 < 3x + 4
6x – 3x < 4 + 5
⇒ 3x <9
⇒ x < 3 as x ∈ I
Therefore Solution Set = { -1, -2, 2, 1, 0….. }
Question -3 Find the solution set of the inequation
x + 5 < 2 x + 3 ; x ∈ R
Graph the solution set on the number line.
Answer -3
x + 5 ≤ 2x + 3
x – 2x ≤ 3 – 5
⇒ -x ≤ -2
⇒ x ≥ 2
∵ x ∈ R , ∴ Solution set = {2, 3, 4, 5, …….}
Hence Solution set on number line
Question -4 If x ∈ R (real numbers) and – 1 < 3 – 2x ≤ 7, find solution set and represent it on a number line.
Answer -4
-1 < 3 – 2x ≤ 7
-1 < 3 – 2x and 3 – 2x ≤ 7
⇒ 2x < 3 + 1 and – 2x ≤ 7 – 3
or 2x < 4 and -2x ≤ 4
⇒ x < 2 and -x ≤ 2
and x ≥ -2 or -2 ≤ x
x ∈ R
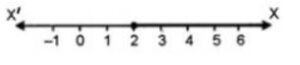
Solution set -2 ≤ x < 2
and Solution set on number line

Question- 5 Solve the inequation :
![]()
Answer -5
(5x + 1)/7 – 4(x/7 + 2/5) ≤ 1.3/5 + (3x – 1)/7
(5x + 1)/7 – 4(x/7 + 2/5) ≤ 8/5 + (3x – 1)/7
Multiplying by L.C.M. of 7 and 5 i.e., 35
25x + 5 – 4 (5x + 14) ≤ 56 + 15x – 5
⇒ 25 + 5 – 20x – 56 ≤ 56 + 15x – 5
⇒ 25x – 20x – 15x ≤ 56 – 5 – 5 + 56
or – 10x ≤ 102
⇒ – x ≤ 102/10
or – x ≤ 51/5
⇒ x ≥ – 51/5
∵ x ∈ R
∴ Therefore Solution set = {x : x ∈ R, x ≥ – 51/5}
Question -6 Find the range of values of a, which satisfy 7 ≤ – 4x + 2 < 12, x ∈ R. Graph these values of a on the real number line.
Answer- 6
7 < – 4x + 2 < 12
⇒ 7 < – 4x + 2 and – 4x + 2 < 12
⇒ 4x ≤ 2 – 7 and – 4x < 12 – 2
or 4x ≤ – 5 and – 4x < 10
⇒ x ≤ -5/4 and – x < 10/4
= x ≤ -5/4 and – x < 5/2
or x > – (5/2)
∵ x ∈ R
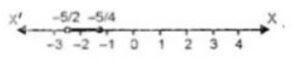
∴ Solution set – 5/2 < x ≤ -5/4
= {x : x ∈ R, – 5/2 < x ≤ – 5/4}
So Solution set on the number line
Question -7 If x ∈ R, solve
![]()
Answer- 7
![]()
⇒ 2x – 3 ≥ x + (1 – x)/3 and x + (1 – x)/3 > 2/5x
⇒ 2x – 3 ≥ (3x + 1 – x)/3 and (3x + 1 – x)/3 > 2/5x
on more solving
⇒ 6x – 9 ≥ 3x + 1 – x and 15x + 5 – 5x > 6x
⇒ 6x – 3x + x ≥ 1 + 9 and 15x – 6x – 5x > – 5
on further simplification
⇒ 4x ≥ 10 and 4x > – 5
⇒ x ≥ 10/4 and x > – 5/4
So , x ≥ 5/2 , ∴ x ≥ 5/2 , because ∵ x ∈ R
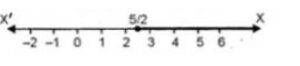
∴ Solution set = {x : x ∈ R, x ≥ 5/2}
Hence Solution set on number line
Question- 8 Find positive integers which are such that if 6 is subtracted from five times the integer then the resulting number cannot be greater than four times the integer.
Answer -8
Let the positive integer = x
According to the problem,
5a – 6 < 4x
⇒ 5a – 4x < 6
⇒ x < 6
Therefore Solution set = {x : x < 6}
= { 1, 2, 3, 4, 5, 6}
Question -9 Find three smallest consecutive natural numbers such that the difference between one-third of the largest and one-fifth of the smallest is at least 3.
Answer- 9
Let first least natural number = x
then second number = x + 1
and third number = x + 2
According to the condition 1/3(x + 2) – 1/5 (x) ≥ 3
5x + 10 – 3x ≥ 45
(Multiplying by 15 the L.C.M. of 2 and 5)
2x ≥ 45 – 10
⇒ 2x ≥ 35
x ≥ 35/2
⇒ x ≥ 17.1/2
∵ x is a natural least number and if ∴ x = 18
∴ find least natural number = 18
Second number = 18 + 1 = 19
And third numbers = 18 + 2 = 20
Hence, least natural numbers are 18, 19, 20
— : End of ML Aggarwal Solutions Linear Inequations Chapter-Test ICSE Class 10 :–
Return to :- ML Aggarwal Solutions for ICSE Class-10
Thanks
Please Share with Your Friends