ML Aggarwal Squares and Squares Roots Exe-3.3 Class 8 ICSE Ch-3 Maths Solutions

ML Aggarwal Squares and Squares Roots Exe-3.3 Class 8 ICSE Ch-3 Maths Solutions. We Provide Step by Step Answer of  Exe-3.3 Questions for Squares and Squares Roots as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-8.

ML Aggarwal Squares and Squares Roots Exe-3.3 Class 8 ICSE Maths Solutions

Board	ICSE
Publications	Avichal Publishig Company (APC)
Subject	Maths
Class	8th
Chapter-3	Squares and Squares Roots
Writer	ML Aggarwal
Book Name	Understanding
Topics	Solution of Exe-3.3 Questions
Edition	2023-2024

Squares and Squares Roots Exe-3.3

ML Aggarwal Class 8 ICSE Maths Solutions

Page-56

Question 1. Find the square roots of the following numbers by the prime factorisation method:

(i) 784

(ii) 441

(iii) 1849

(iv) 4356

(v) 6241

(vi) 8836

(vii) 8281

(viii) 9025

Answer:

(i) We know that

Square root of 784

It can be written as

So we get

= 2 × 2 × 7

= 28

(ii) We know that

Square root of 441

It can be written as

So we get

= 3 × 7

= 21

(iii) We know that

Square root of 1849

It can be written as

= 43

(iv) We know that

Square root of 4356

It can be written as

So we get

= 2 × 3 × 11

= 66

(v) We know that

Square root of 6241

It can be written as

= 79

(vi) We know that

Square root of 8836

So we get

= 2 × 47

= 94

(vii) We know that

Square root of 8281

So we get

= 7 × 13

= 91

(viii) We know that

Square root of 9025

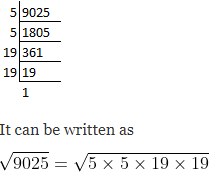
So we get

= 5 × 19

= 95

Question 2. Find the square roots of the following numbers by the prime factorisation method:

(i) 9 (67/121)

(ii) 17 (13/36)

(iii) 1.96

(iv) 0.0064

Answer:

(i) 9 67/121 = (9 × 121 + 67)/ 121

By further calculation

= (1089 + 67)/ 121

= 1156/121

By squaring, we get

So we get

= (2 × 17)/ 11

= 34/11

= 3 1/11

(ii) 17 13/36 = (17 × 36 + 13)/ 36

By further calculation

= (612 + 13)/ 36

= 625/36

By squaring we get

So we get

= (5 × 5)/ (2 × 3)

= 25/6

= 4 1/6

(iii) 1.96 = 196/100

By squaring, we get

So we get

= (2 × 7)/ (2 × 5)

= 14/10

= 1.4

(iv) 0.0064 = 64/10000

By squaring, we get

So we get

= (2 × 2 × 2)/ (2 × 2 × 5 × 5)

= 8/100

= 0.08

Question 3. For each of the following numbers, find the smallest natural number by which it should be multiplied so as to get a perfect square. Also, find the square root of the square number so obtained:

(i) 588

(ii) 720

(iii) 2178

(iv) 3042

(v) 6300

Answer:

(i) 588 = 2 × 2 × 3 × 7 × 7

By pairing the same kind of factors, one factor, 3 is left unpaired.

So to make it a pair, we must multiply it by 3

Required least number = 3

Square root of 588 × 3 = 1764

Here

2 × 3 × 7 = 42

(ii) 720 = 2 × 2 × 2 × 2 × 3 × 3 × 5

By pairing the same kind of factors, one factor, 5 is left unpaired.

So to make it a pair, we must multiply it by 5

Required least number = 5

Square root of 720 × 5 = 3600

Here

2 × 2 × 3 × 5 = 60

(iii) 2178 = 2 × 3 × 3 × 11 × 11

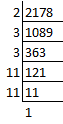
By pairing the same kind of factors, one factor, 2 is left unpaired.

So to make it a pair, we must multiply it by 2

Required least number = 2

Square root of 2178 × 2 = 4356

Here

2 × 3 × 11 = 66

(iv) 3042 = 2 × 3 × 3 × 13 × 13

By pairing the same kind of factors, one factor 2 is left unpaired

So to make it a pair, we must multiply it by 2

Required least number = 2

Square root of 3042 × 2 = 6084

Here

2 × 3 × 13 = 78

(v) 6300 = 2 × 2 × 3 × 3 × 5 × 5 × 7

By pairing the same kind of factors, one factor 7 is left unpaired

So, to make it a pair, we must multiply it by 7

Required least number = 7

Square root of 6300 × 7 = 44100

Here

2 × 3 × 5 × 7 = 210

Question 4. For each of the following numbers, find the smallest natural number by which it should be divided so that this quotient is a perfect square. Also, find the square root of the square number so obtained:

(i) 1872

(ii) 2592

(iii) 3380

(iv) 16224

(v) 61347

Answer:

(i) 1872 = 2 × 2 × 2 × 2 × 3 × 3 × 13

By pairing the same kind of factors, one factor 13 is left unpaired

Required least number = 13

The number 1872 should be divided by 13 so that the resultant number will be a perfect square

Resultant number = 1872 ÷ 13 = 144

Square root = 2 × 2 × 3 = 12

(ii) 2592 = 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3

By pairing the same kind of factors, one factor 2 is left unpaired

Required least number = 2

The number 2592 should be divided by 2 so that the resultant number will be a perfect square

Resultant number = 2592 ÷ 2 = 1296

Square root = 2 × 2 × 3 × 3 = 36

(iii) 3380 = 2 × 2 × 5 × 13 × 13

By pairing the same kind of factors, one factor 5 is left unpaired

Required least number = 5

The number 3380 should be divided by 5 so that the resultant number will be a perfect square

Resultant number = 3380 ÷ 5 = 676

Square root = 2 × 13 = 26

(iv ) 16224 = 2 × 2 × 2 × 2 × 2 × 3 × 13 × 13

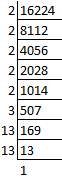
By pairing the same kind of factors, two factors 2 and 3 is left unpaired

Required least number = 2 × 3 = 6

The number 16224 should be divided by 6 so that the resultant number will be a perfect square

Resultant number = 16224 ÷ 6 = 2704

Square root = 2 × 2 × 13 = 52

(v) 61347 = 3 × 11 × 11 × 13 × 13

By pairing the same kind of factors, one factor 3 is left unpaired

Required least number = 3

The number 61347 should be divided by 3 so that the resultant number will be a perfect square

Resultant number = 61347 ÷ 3 = 20449

Square root = 11 × 13 = 143

Question 5. Find the smallest square number that is divisible by each of the following numbers:

(i) 3, 6, 10, 15

(ii) 6, 9, 27, 36

(iii) 4, 7, 8, 16

Answer:

(i) 3, 6, 10, 15

The number which is divisible by

3, 6, 10, 15 = LCM of 3, 6, 10, 15

It can be written as

So we get

= 2 × 3 × 5

= 30

(ii) 6, 9, 27, 36

The number which is divisible by

6, 9, 27, 36 = LCM of 6, 9, 27, 36

It can be written as

So we get

= 3 × 3 × 2 × 2 × 3

= 108

Here the smallest square

= 108 × 3

= 324

(iii) 4, 7, 8, 16

The number which is divisible by

4, 7, 8, 16 = LCM of 4, 7, 8, 16

It can be written as

So we get

= 2 × 2 × 2 × 2 × 7

= 112

Here the smallest square

= 112 × 7

= 784

Question 6. 4225 plants are to be planted in a garden in such a way that each row contains as many plants as the number of rows. Find the number of rows and the number of plants in each row.

Answer:

Total number of plants = 4225

Number of rows = Number of plants in each row

So the number of rows = square root of 4225

= 5 × 13

= 65

Hence, the number of rows is 65, and the number of plants in each row is 65.

Question 7. The area of a rectangle is 1936 sq. m. If the length of the rectangle is 4 times its breadth, find the dimensions of the rectangle.

Answer:

Area of rectangle = 1936 sq. m

Take breadth = x m

Length = 4x m

4x² = 1936

x² = 1936/4 = 484

= 2 × 11

= 22

Length = 4x = 4 × 22 = 88 m

Breadth = x = 22 m

Question 8. In a school, a P.T. teacher wants to arrange 2000 students in the form of rows and columns for P.T. display. If the number of rows is equal to the number of columns and 64 students cannot be accommodated in this arrangement, find the number of rows.

Answer:

Total number of students in a school = 2000

The P.T. teacher arranges in such a way that

No. of rows = no. of students in each row

So 64 students are left

Required number of students = 2000 – 64 = 1936

No. of rows = √1936

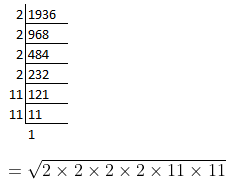
= 2 × 2 × 11

= 44

---

Squares and Squares Roots Exe-3.3

ML Aggarwal Class 8 ICSE Maths Solutions

Page-57

Question 9. In a school, the students of class VIII collected ₹2304 for a picnic. Each student contributed as many rupees as the number of students in the class. Find the number of students in the class.

Answer:

Amount collected for picnic = ₹2304

No. of students = no. of rupees contributed by each student = √2304

By further calculation

= 2 × 2 × 2 × 2 × 34= 48

Therefore, the number of students in class VIII is 4811.

Question 10. The product of two numbers is 7260. If one number is 15 times the other number, find the numbers.

Answer:

Product of two numbers = 7260

Consider one number = x

Second number = 15x

15x × x = 7260

15x² = 7260

x² = 7260/15 = 484

= 2 × 11

= 22

One number = 22

Second number = 22 × 15 = 330

Question 11. Find three positive numbers in the ratio 2: 3: 5, the sum of whose squares is 950.

Answer:

Ratio of three positive numbers = 2: 3: 5

Sum of their squares = 950

First number = 2x

Second number = 3x

Third number = 5x

It can be written as

(2x)²+ (3x)² + (5x)² = 950

4x² + 9x² + 25x² = 950

38x² = 950

X² = 950/38 = 25

x = √25 = 5

First number = 2 × 5 = 10

Second number = 3 × 5 = 15

Third number = 5 × 5 = 25

Question 12.  The perimeter of two squares is 60 metres and 144 metres, respectively. Find the perimeter of another square equal in area to the sum of the first two squares.

Answer:

Perimeter of first square = 60 m

Side = 60/4 = 15 m

Perimeter of second square = 144 m

Side = 144/4 = 36 m

So the sum of perimeters of two squares = 60 + 144 = 204 m

Sum of areas of these two squares = 15² + 36²

= 225 + 1296

= 1521 m²

Area of third square = 1521 m²

= 3 × 13

= 39 m

Here

Perimeter = 4 × side

Substituting the values

= 4 × 39

= 156 m

—  : End of ML Aggarwal Squares and Squares Roots Exe-3.3 Class 8 ICSE Maths Solutions :–

Return to –  ML Aggarwal Maths Solutions for ICSE Class -8

Thanks

Please Share with Your Friends