ML Aggarwal Squares and Squares Roots Exe-3.4 Class 8 ICSE Ch-3 Maths Solutions. We Provide Step by Step Answer of Exe-3.4 Questions for Squares and Squares Roots as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-8.
ML Aggarwal Squares and Squares Roots Exe-3.4 Class 8 ICSE Maths Solutions
| Board | ICSE |
| Publications | Avichal Publishig Company (APC) |
| Subject | Maths |
| Class | 8th |
| Chapter-3 | Squares and Squares Roots |
| Writer | ML Aggarwal |
| Book Name | Understanding |
| Topics | Solution of Exe-3.4 Questions |
| Edition | 2023-2024 |
Squares and Squares Roots Exe-3.4
ML Aggarwal Class 8 ICSE Maths Solutions
Page-62
Question 1. Find the square root of each of the following by division method:
(i) 2401
(ii) 4489
(iii) 106929
(iv) 167281
(v) 53824
(vi) 213444
Answer:
(i) √2401 = 49
By division method

(ii) √4489 = 67
By division method

(iii) √106929 = 327
By division method

(iv) √167281 = 409
By division method

(v) √53824 = 232
By division method

(vi) √213444 = 462
By division method

Squares and Squares Roots Exe-3.4
ML Aggarwal Class 8 ICSE Maths Solutions
Page-63
Question 2. Find the square root of the following decimal numbers by division method:
(i) 51.84
(ii) 42.25
(iii) 18.4041
(iv) 5.774409
Answer:
(i) √51.84 = 7.2
By division method

(ii) √42.25 = 6.5
By division method

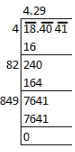
(iii) √18.4041 = 4.29
By division method
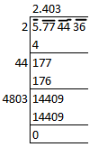
(iv) √5.774409 = 2.403
By division method
Question 3. Find the square root of the following numbers correct to two decimal places:
(i) 645.8
(ii) 107.45
(iii) 5.462
(iv) 2
(v) 3
Answer:
(i) √645.8 = 25.41
It can be written as

(ii) √107.45 = 10.36
It can be written as

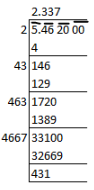
(iii) √5.462 = 2.337 = 2.34
It can be written as
(iv) √2 = 1.41
It can be written as

(v) √3 = 1.73
It can be written as

Question 4. Find the square root of the following fractions correct to two decimal places:
(i) 11(3/8)
(ii) 5(5/11)
(iii) 7(1/3)
Answer: update soon
Question 5. Find the least number which must be subtracted from each of the following numbers to make them a perfect square. Also, find the square root of the perfect square number so obtained:
(i) 2000
(ii) 984
(iii) 8934
(iv) 11021
Answer:
(i) 2000
We know that

By taking the square root, 64 is left as the remainder
Subtracting 64 from 2000
We get 1936 which is a perfect square, and its square root is 44.
(ii) 984
We know that

By taking the square root, 23 is left as the remainder
Subtracting 23 from 984
We get 961 which is a perfect square, and its square root is 31.
(iii) 8934
We know that

By taking the square root, 98 is left as the remainder
Subtracting 98 from 894
We get 8934 – 98 = 8836 which is a perfect square, and its square root is 94.
(iv) 11021
We know that

By taking the square root, 205 is left as the remainder
Subtracting 205 from 11021
We get 11021 – 205 = 10816 which is a perfect square, and its square root is 104.
Question 6. Find the least number which must be added to each of the following numbers to make them a perfect square. Also, find the square root of the perfect square number so obtained:
(i) 1750
(ii) 6412
(iii) 6598
(iv) 8000
Answer:
(i) 1750
We know that

By taking the square root
412 is less than 1750
So by taking 422
164 – 150 = 14 less
Adding 14, we get a square of 42 which is 1764.
(ii) 6412
We know that

By taking the square root
802 is less than 6412
So by taking 812
161 – 12 = 14 less
Adding 149, we get a square of 81 which is 6561.
(iii) 6598
We know that
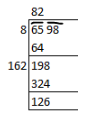
By taking the square root
812 is less than 6598
So by taking 822
324 – 198 = 126 less
Adding 126, we get a square of 82 which is 6724.
(iv) 8000
We know that

By taking the square root
892 is less than 8000
So by taking 902
8100 – 8000 = 100 less
Adding 100, we get a square of 90 which is 8100.

Question 7. Find the smallest four-digit number, which is a perfect square.
Answer:
It is given that
Smallest four–digit number = 1000
We know that

By taking the square root, we find that 39 is left.
If we subtract any number from 1000, we get 3 digit number
Take 322 = 1024
Here 1024 – 1000 = 24 is to be added to get a perfect square of least 4 digit number
Therefore, the required 4-digit smallest number is 1024.
Question 8. Find the greatest number of six digits, which is a perfect square.
Answer:
It is given that
Greatest six-digit number = 999999
We know that

By taking the square root, we find that 1998 is left
If we subtract 1998 from 999999, we get 998001 which is a perfect square.
Therefore, the required six-digit greatest number is 998001.
Question 9. In a right triangle ABC, ∠B = 900.
(i) If AB = 14 cm, BC = 48 cm, find AC.
(ii) If AC = 37 cm, BC = 35 cm, find AB.
Answer:
(i) In a right-angled triangle ABC
It is given that
AB = 14 cm and BC = 48 cm
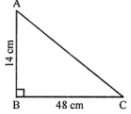
Using Pythagoras theorem
AC2 = AB2 + BC2
Substituting the values
= 142 + 482
By further calculation
= 196 + 2304
= 2500
So we get
AC = √2500 = 50 cm

(ii) In a right triangle, ABC
B = 900, AC = 37 cm, BC = 35 cm
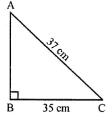
Using Pythagoras Theorem
AC2 = AB2 + BC2
Substituting the values
372 = AB2 + 352
By further calculation
1369 = AB2 + 1225
AB2 = 1369 – 1225 = 144
So we get
AB = √144 = 12 cm
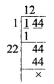
Question 10. A gardener has 1400 plants. He wants to plant these in such a way that the number of rows and columns remains the same. Find the minimum number of plants he needs more for this.
Answer:
It is given that
Total number of plants = 1400
We know that

Here
Number of columns = Number of rows
By taking the square root of 1400
372 < 1400
So take 382 = 1444
We need 1444 – 1400 = 44 plants more
Therefore, the minimum number of plants he needs more for this is 44.
Question 11. There are 1000 children in a school. For a P.T. drill, they have to stand in such a way that the number of rows is equal to the number of columns. How many children would be left out in this arrangement?
Answer:
It is given that
No. of total children in a school = 1000
For a P.T. drill, children have to stand in such a way that
No. of rows = No. of columns
Take the square root of 1000
39 is left as the remainder
Left out children = 39

Hence, 39 children would be left out in this arrangement.
Question 12. Amit walks 16 m south from his house and turns east to walk 63 m to reach his friend’s house. While returning, he walks diagonally from his friend’s house to reach back to his house. What distance did he walk while returning?
Answer:
It is given that
Amit walks 16 m south from his house and turns east to walk 63 m to reach his friend’s house
Consider O as the house and A and B as the places
OA = 16 m, AO = 63 m

Using Pythagoras theorem
OB2 = OA2 + AB2
Substituting the values
= 162 + 632
By further calculation
= 256 + 3969
= 4225
So we get
OB = √4225 = 65

Therefore, Amit has to walk 65 m to reach his house.
Question 13. A ladder 6 m long leaned against a wall. The ladder reaches the wall to a height of 4.8 m. Find the distance between the wall and the foot of the ladder.
Answer:
It is given that
Length of ladder = 6 m
The ladder reaches the wall to a height of 4.8 m
Consider AB as the ladder and AC as the height of the wall
AB = 6 m and AC = 4.8 m
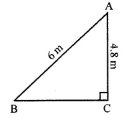
The distance between the foot of the ladder and the wall is BC
Using the Pythagoras theorem,
AB2 = AC2 + BC2
Substituting the values
62 = 4.82 + BC2
By further calculation
BC2 = 62 – 4.82
BC2 = 36 – 23.04 = 12.96
So we get
BC = √12.96 = 3.6 m

Hence, the distance between the wall and the foot of the ladder is 3.6 m.
— : End of ML Aggarwal Squares and Squares Roots Exe-3.4 Class 8 ICSE Maths Solutions :–
Return to – ML Aggarwal Maths Solutions for ICSE Class -8
Thanks
Please Share with Your Friends