ML Aggarwal Visualising Solid Shapes Check Your Progress Class 8 ICSE Ch-17 Maths Solutions. We Provide Step by Step Answer of Check Your Progress Questions for Visualising Solid Shapes as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-8.
ML Aggarwal Visualising Solid Shapes Check Your Progress Class 8 ICSE Maths Solutions
| Board | ICSE |
| Publications | Avichal Publishig Company (APC) |
| Subject | Maths |
| Class | 8th |
| Chapter-17 | Visualising Solid Shapes |
| Writer | ML Aggarwal |
| Book Name | Understanding |
| Topics | Solution of Check Your Progress |
| Edition | 2023-2024 |
Visualising Solid Shapes Check Your Progress
ML Aggarwal Class 8 ICSE Maths Solutions
Page-289
Question 1. Write the number of faces, vertices and edges of a
(i) hexagonal pyramid
(ii) octagonal pyramid
(iii) decagonal pyramid
(iv) nonagonal pyramid
(v) heptagonal prism
(vi) decagonal prism.
Answer:
| Faces | Vertices | Edges | |
| (i) hexagonal pyramid | 7 | 7 | 12 |
| (ii) octagonal pyramid | 9 | 9 | 16 |
| (iii) decagonal pyramid | 11 | 11 | 20 |
| (iv) nonagonal pyramid | 10 | 10 | 18 |
| (v) heptagonal prism | 9 | 14 | 21 |
| (vi) decagonal prism | 12 | 20 | 30 |
Question 2. Give three examples of 3-dimensional shapes around you which are the combinations of 2 or more 3-dimensional shapes.
Answer:
3-dimensional shapes which are the combination of
2 or more 3-dimensional shapes.
(i) A funnel: Combination of cone and cylinder.
(ii) A toy: Combination of a cone and hemisphere.
(iii) An ice-cream cone: Combination of a cone and hemisphere.
(iv) A circus tent: Combination of a cylinder and a cone.
Question 3. Give two examples of solids which are not polyhedrons.
Answer:
Sides which are not polyhedron:
(i) Cylinder
(ii) Sphere
Question 4. Why a pentagonal pyramid having all its edges congruent cannot be a regular polyhedron?
Answer:
A pentagonal pyramid having all its edges congruent cannot be a regular
polyhedron because all the vertices of it are not formed by the same number of faces.
Question 5. In a polyhedron, if F = 8 and V = 12 then find the number of edges.
Answer:
In a polyhedron,
F = 8, V = 12, then edges
F + V = E + 2
⇒ E = F + V- 2
⇒ Edges = 8 + 12 – 2 = 18
Question 6. Verify Euler’s formula for the following figures:
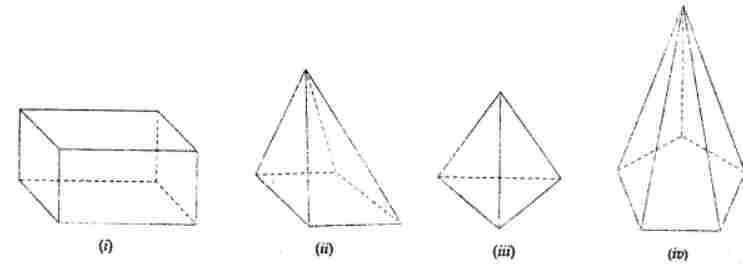
Answer:
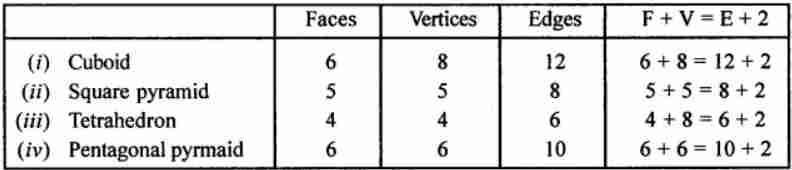
— End of Visualising Solid Shapes Check Your Progress Class 8 ICSE Maths Solutions :–
Return to : – ML Aggarwal Maths Solutions for ICSE Class -8
Thanks


