Model Question Paper-3 ML Aggarwal Class-7 ICSE Maths

Model Question Paper-3 Solved Class-7 ML Aggarwal ICSE Mathematics . APC Understanding Mathematics for ICSE Class-7 Model Question Paper-3 Solutions based on Chapter-1 to 9. Visit official Website CISCE for detail information about ICSE Board Class-7 Mathematics.

Model Question Paper-3 ML Aggarwal Class-7 ICSE Maths

–: Select Topic :–

ML Aggarwal Class-7 ICSE Maths Model Question Paper 3

( based on chapter-1 to 9)

Time Allowed-1 hour

max mark-25

General Instructions

All questions are compulsory.
The question paper consists of 29 questions divided into four sections A, B, C and D.
Section A comprises of 8 questions of 1 mark each.
Section B comprises of 6 questions of 2 marks each.
Section C comprises of 10 questions of 4 marks each and
Section D comprises of 5 questions of 6 marks each.
Question numbers 1 to 8 in Section A is multiple choice questions where you are to select one correct option out of the given four.

Section – A

Choose the correct answer from the given four option (1-2)

Question 1

Question 1.
The number of integers between -16 and 5 is
(a) 19
(b) 20
(c) 21
(d) 22

Answer

Number of integer between -16 and 5 is -15 to 4 = 20 (b)

Question 2.
50 m 5 cm is the same as
(a) 50.5 m
(b) 50.05 m
(c) 50.005 m
(d) 5.05 m

Answer

50 m 5 cm = 50.05 m (b)

Question 3

……………..

Answer

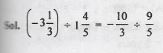
Question 4

The number 5,540,000,000,000 in the scientific notation can be written as:
(a) 554 × 10¹⁰
(b) 55.4 × 10¹¹
(c) 5.54 × 10¹²
(d) 5.54 × 10¹¹

Answer

5,540,000,000,000 = 5.54 × 10¹² (c)

Question 5.

The number of unlike terms in the expression 5x²y – 2xy² – 2yx² + 3y(xy + y²) + 7 is
(a) 3
(b) 4
(c) 5
(d) 6

Answer

Number of unlike terms
5x²y – 2xy² – 2yx² + 3y(xy + y²) + 7
= 5x²y – 2xy² – 2yx² + 3xy² + 3y³ + 7
= 3x²y + xy² + 3y³ + 7 = 4 (b)

Question 6

x = -2 is a solution of the equation
(a) 2x + 5 = 9
(b) 3x – 1 = 5
(c) 4x + 3 = 1
(d) 5x + 12 = 2

Answer

5x + 12 = 5 × (-2) + 12 = -10 + 12 = 2 (d)

Question 7

The ratio of the number of girls to the number of boys in a class is 5 : 4. If there are 16 boys in the class, then the number of students in the class is
(a) 20
(b) 32
(c) 36
(d) 45

Answer

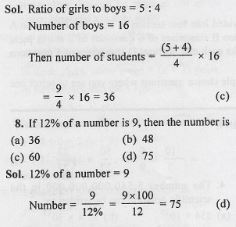
Section – B

Question numbers 9 to 14 are of 2 marks each.

Question 9.

Using suitable properties, evaluate:
238 × (-44) + (-238) × 56.

Answer

238 × (-44) + (-238) × 56
= 238 × (-44) – (238) × 56
= 238 (-44 – 56)
= 238 × (-100)
= -23800

Question 10

State whether each of the following statement is true or false for the sets P and Q where P = {letters of TITLE} and Q = {letters of LITTLE}
(i) P ↔ Q
(ii) P = Q
Solution:
P = {letters of TITLE} = {T, I, L, E}
Q = {letters of LITTLE} = {L, I, T, E}
(i) P ↔ Q – True
(ii) P = Q – True

Question 11

Evaluate: -3 $\frac { 3 }{ 8 }$ – (-2 $\frac { 1 }{ 6 }$ )

Answer

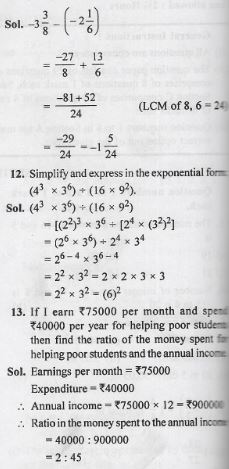
Ans 11 to 13 Model Question Paper 3 Linear Equations and Linear Inequalities ML Aggarwal Class-7 ICSE Mathematics Solutions-compressed

Question 14

If ₹ 4000 amounts to ₹ 5000 in 2 years, find the rate of simple interest per annum.
Solution:
Principal (P) = ₹ 4000
Amount (A) = ₹ 5000
S.I. = A – P = ₹ 5000 – ₹ 4000 = ₹ 1000
Time (T) = 2 years

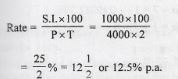
Section – C

Question numbers 15 to 24 are of 4 marks each.

Question 15.
Simplify:

……………….

Answer

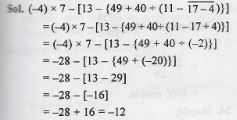
Question 16

Vikram’s monthly salary is ₹ 12750. He spends $\frac { 1 }{ 5 }$ of his salary on food and out of the remaining, he spends $\frac { 1 }{ 4 }$ on rent and $\frac { 1 }{ 6 }$ on the education of children. Find
(i) how much he spends on each item?
(ii) how much money is still left with him?

Answer

Monthly salary of Vikram = ₹ 12750
Spent on food = $\frac { 1 }{ 5 }$ of 12750 = ₹ 2550
Remaining salary = ₹ 12750 – ₹ 2550 = ₹ 10200
Spent on rent = $\frac { 1 }{ 4 }$ of ₹ 10200 = ₹ 2550
Spent on Education = $\frac { 1 }{ 6 }$ × ₹ 10200 = ₹ 1700
Amount still left with him = ₹ 10200 – ₹ (2550 + 1700)
= ₹ 10200 – ₹ 4250
= ₹ 5950

Question 17

Insert five rational numbers between $\frac { -2 }{ 5 }$ and $\frac { -1 }{ 3 }$

Answer

Question 18

Afzal can walks 5 $\frac { 3 }{ 4 }$ km in one hour. How much distance will he cover in 2 hours 40 minutes? What are the health advantages of having a brisk walk?

Answer

In one hour, Afzal can walk = 5 $\frac { 3 }{ 4 }$ = $\frac { 23 }{ 4 }$

Question 19

If a vehicle covers a distance of 57.72 km in 3.7 litres of petrol. How much distance will it cover in one litre of petrol?
Solution:
In 3.7 litres of petrol a vehicle can travel = 57.72 km
It will cover in 1 litre = $\frac { 57.72 }{ 3.7 }$
= 15.6 km

Answer

Question 22

Solve the equation: 3(2x – 1) – 2(2 – 5x) = 1

Answer

3(2x – 1) – 2(2 – 5x) = 1
⇒ 6x – 3 – 4 + 10x = 1
⇒ 16x – 7 = 1
⇒ 16x = 1 + 7 = 8
⇒ x = $\frac { 8 }{ 16 }$ = $\frac { 1 }{ 2 }$

Question 23

If 74% of the population of a village is illiterate and the number of literate people is 2158, then find the population of the village.

Answer

Section -D

Question numbers 25 to 29 are of 6 marks each.

Question 25.
If we represent the distance above the ground by a positive rational number and that below the ground by a negative rational number, then answer the following question:
An elevator descends into a mine shaft at the rate of 4 $\frac { 3 }{ 4 }$ metre per minute. If it begins to descend from 7 $\frac { 1 }{ 2 }$ metre above the ground, what will be its position after 18 minutes from the ground?

Answer

Speed of elevator into the mine = 4 $\frac { 3 }{ 4 }$ = $\frac { 19 }{ 4 }$ m/min
Time taken = 18 m
Total distance covered = $\frac { 19 }{ 4 }$ × 18 = $\frac { 171 }{ 2 }$ m = 85.5 m
Distance above the ground = 7.5 m
Distance below the ground = 85.7 – 7.5 = 78 m
It is below the ground.
It will be = -78 m

Question 26

In a competition, the question paper consists of 25 questions. 4 marks are awarded for every correct answer, 2 marks are deducted for every incorrect answer and no marks for not attempting a question. If Vaishali scored 58 marks and got 17 correct answers, how many questions she attempted incorrectly? How many questions she did not attempt?

Answer

Total number of questioins = 25
For correct answer = 4 marks per question
Deduction of 2 marks for incorrect answer
No marks for unattemtped question
Vaishali got 58 marks and got 17 correct questions
Let x be the questions of wrong answer
17 × 4 – 2x + (25 – 17 – x) × 0 = 58
68 – 58 = 2x + 0
2x = 10
x = 5
Number of wrong answer questions = 5
and number of questions not attempted = 25 – 17 – 5 = 3

Question 27.

Divide ₹ 216000 into two parts such that one-fourth of one part is equal to one-fifth of the other part. Find the two parts.

Answer

Amount = ₹ 216000
Let $\frac { 1 }{ 4 }$ of one part = $\frac { 1 }{ 5 }$ of second part = x
First part = 4x
Second part = 5x
4x + 5x = 216000
⇒ 9x = 216000
⇒ x = $\frac { 216000 }{ 9 }$ = 24000
First part = ₹ 24000 × 4 = ₹ 96000
Second part = ₹ 24000 × 5 = ₹ 120000