Motion in One Dimension Exe-2C Equations of Motion Numericals Type for Class-9 ICSE Concise Physics. There is the solutions of Numericals type Questions of your latest textbook which is applicable in 2023-24 academic session. Visit official Website CISCE for detail information about ICSE Board Class-9.
Motion in One Dimension Exe-2 C Equations of Motion Numericals
(ICSE Class – 9 Physics Concise Selina Publishers)
| Board | ICSE |
| Class | 9 |
| Subject | Physics |
| Writer / Publication | Concise selina Publishers |
| Chapter-2 | Motion in One Dimension |
| Exe – 2 C | Equations of Motion |
| Topics | Solution of Exe-2(C) Numericals |
| Academic Session | 2023-2024 |
Exe-2C Equations of Motion Numericals Type
Ch-2 Motion in One Dimension Physics Class-9 ICSE Concise
Page 60
Question 1. A body starts from rest with uniform acceleration 2 m s-2. Find the distance covered by the body in 2 s.
Answer:
Initial velocity u = 0
Acceleration a = 2 m/s2
Time t = 2 s
Let ‘S’ be the distance covered.
Using the second equation of motion,
S = ut + (1/2) at2
S = 0 + (1/2) (2) (2) 2
S = 4 m
Question 2. A body starts with an initial velocity of 10m s-1 and acceleration 5 m s-2. Find the distance covered by it in 5 s.
Answer:
Initial velocity u = 10 m/s
Acceleration a = 5 m/s2
Time t = 5s
Let ‘S’ be the distance covered.
Using the second equation of motion,
S = ut + (1/2) at2
S = (10)(5) + (1/2) (5) (5) 2
S = 50 + 62.5
S = 112.5 m
Question 3. A vehicle is accelerating on a straight road. Its velocity at any instant is 30 km/h. After 2s, it is 33.6 km/h, and after further 2 s, it is 37.2 km/h. Find the acceleration of the vehicle in m s-2. Is the acceleration uniform?
Answer:
Acceleration = Change in velocity/time taken
In the first two seconds,
Acceleration = [(33.6 – 30)/2] km/h2
= 1.8 km/h2
= 0.5 m/s2 …(i)
In the next two seconds,
Acceleration = [(37.2 – 33.6)/2] km/h2
= 1.8 km/h2
= 0.5 m/s–2…(ii)
From (i) and (ii), we can say that the acceleration is uniform.
(Motion in One Dimension Exe-2C Numericals Class-9 ICSE)
Question 4. A body, initially at rest, starts moving with a constant acceleration 2 m s-2. Calculate: (i) the velocity acquired and (ii) the distance travelled in 5 s.
Answer:
Initial velocity u = 0 m/s
Acceleration a = 2 m/s2
Time t = 5 s
(i) Let ‘v’ be the final velocity.
Then, (v – u)/5 = 2
v = 10 m/s-1
(ii) Let ‘s’ be the distance travelled.
Using the third equation of motion,
v2 – u2 = 2as
We get,
(10) 2 – (0) 2 = 2(2) (s)
Thus, s = (100/4) m = 25 m
Question 5. A bullet initially moving with a velocity 20 m/s strikes a target and comes to rest after penetrating a distance 10 cm into the target. Calculate the retardation caused by the target.
Answer :
Initial velocity u = 20 m/s
Final velocity v = 0
Distance travelled s = 10 cm = 0.1 m
Let acceleration be ‘a’.
Using the third equation of motion,
v2 – u2 = 2as
We get,
(0) 2 – (20) 2 = 2(a) (0.1)
a = -(400/0.2) m/s2
a = -2000 m/s2
Thus, retardation = 2000 m/s-2
(Motion in One Dimension Exe-2C Numericals Class-9 ICSE)
Question 6. A train moving with a velocity of 20 m s-1 is brought to rest by applying brakes in 5 s. Calculate the retardation.
Answer :
Initial velocity u = 20 m/s
Final velocity v = 0
Time taken t = 5 s
Let acceleration be ‘a’.
Using the first equation of motion,
v = u + at
0 = 20 + 5a
a = -4 m/s-2
Thus, retardation = 4 m/s-2
Question 7. A train travels with a speed of 60 km h-1 from station A to station B and then comes back with a speed 80 km h-1 from station B to station A.
Find :
(i) The average speed
(ii) The average velocity of the train
Answer :
Let ‘s’ be the distance between stations A and B.
(i) Average speed = Total distance/total time taken
Here, total distance = s + s = 2s
Total time taken = Time taken to travel from A to B + Time taken to travel from B to A.
= [(s/ 60) + (s/ 80)] s
= [ 140 s / 4800] s
and Average speed =2s/(140s/4800)
=(2×4800) /140
=68.57km/h
(ii) Average velocity = Displacement/total time taken
Because the train starts and ends at the same station, the displacement is zero. Thus the average velocity is zero.
Exe-2C Equations of Motion Numericals Type
Motion in One Dimension Exe-2C Numericals Class-9 ICSE
Page 60
Question 8. A train is moving with a velocity of 90 km h-1. When the brakes are applied, retardation produced is 0.5 ms-2.
Find:
(i) The velocity after 10 s
(ii) The time taken by the train to come to rest.
Answer:
Initial velocity u = 90 km/h = 25 m/s
Final velocity v = 0 m/s
Acceleration a = -0.5 m/s2
(i) Let ‘V’ be the velocity after time t = 10 s
Using the first equation of motion,
v = u + at
We get,
V = 25 + (-0.5) (10) m/s
V = 25 – 5 = 20 m/s-1
(ii) Let t’ be the time taken by the train to come to rest.
Using the first equation of motion,
v = u + at
We get,
t’ = [(0 – 25)/ (-0.5)] s
t’ = 50 s
Question 9. A car travels a distance 100 m with constant acceleration and average velocity of 20 ms-1. The final velocity acquired by the car is 25 ms-1.
Find:
(i) The initial velocity.
(ii) Acceleration of the car.
Answer:
Distance travelled s = 100 m
Average velocity V = 20 m/s
Final velocity v = 25 m/s
(i) Let u be the initial velocity.
Average velocity = (Initial velocity + Final velocity)/2
V = (u + v)/2
20 = (u + 25)/2
u = 40 – 25 = 15 m/s-1
(ii) Let ‘a’ be the acceleration of the car.
Using the third equation of motion,
v2 – u2 = 2as
We get,
(25) 2 – (15) 2 = 2 (a) (100)
625 – 225 = 200 a
a = (400/200) m/s2 = 2 m/s-2
Question 10. When brakes are applied to a bus, retardation produced is 25 cm s-2 and the bus takes 20 s to stop.
Calculate :
(i) The initial velocity of the bus
(ii) The distance travelled by the bus during this time.
Answer:
Final velocity v = 0
Acceleration = -25 cm/s2 or -0.25 m/s2
Time taken t = 20 s
(i) Let ‘u’ be the initial velocity.
Using the first equation of motion,
v = u + at
We get,
u = v – at
u = 0 – (-0.25)(20) = 5 m/s-1
(ii) Let ‘s’ be the distance traveled.
Using the third equation of motion,
v2 – u2 = 2as
We get,
(0) 2 – (5)2 = 2 (-0.25) (s)
s = (25/0.5) = 50 m.
Question 11. A body moves from rest with uniform acceleration and travels 270 m in 3 s. Find the velocity of the body at 10 s after the start.
Answer:
Initial velocity u = 0 m/s
Distance travelled s = 270 m
Time taken to travel s distance = 3 s
Let ‘a’ be the uniform acceleration.
Using the second equation of motion,
S = ut + (1/2) at2
We get,
270 = 0 + (1/2) a (3)2
270 = 9a/2
a = 60 m/s2
Let v be the velocity of the body 10 s after the start.
Using the first equation of motion, we get
v = u + at
v = 0 + (60)(10) = 600 m/s-1
(Motion in One Dimension Exe-2C Numericals Class-9 ICSE)
Question 12. A body moving with a constant acceleration travels the distances 3 m and 8 m, respectively in 1 s and 2 s.
Calculate:
(i) The initial velocity.
(ii) The acceleration of body.
Answer:
Let the constant acceleration with which the body moves be ‘a’.
Given, the body travels distance S1 = 3 m in time t1 = 1 s.
Same body travels distance S2 = 8 m in time t2 = 2 s.
(i) Let ‘u’ be the initial velocity.
Using the second equation of motion,
S = ut + (1/2) at2
Substituting the value for S1 and S2, we get
(ii) Putting u = 2 m/s in the equation
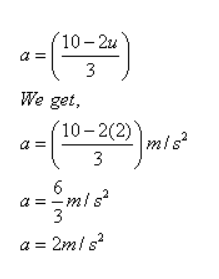
Question 13. A car travels with uniform velocity of 25 m s-1 for 5 s. The brakes are then applied and the car is uniformly retarded and comes to rest in further 10 s. Find: (i) The distance which the car travels before the brakes are applied, (ii) Retardation and (iii) The distance travelled by the car after applying the brakes.
Answer:
Initial velocity u = 25 m/s
Final velocity v = 0
(i) Before the brakes are applied, let S be the distance travelled.
Distance = Speed × time
S = (25) × (5) m
S = 125 m
(ii) Acceleration = (Final velocity – Initial velocity)/Time taken
= [(0 – 25)/15] ms-2
and = (-5/2) ms-2
so = -2.5 ms-2
Therefore, retardation = 2.5 ms-2
(iii) After applying brakes, the time taken to come to stop = 10 s
Let S’ be the distance travelled after applying the brakes.
Initial velocity u = 25 m/s
Final velocity v = 0
Using the third equation of motion,
v2 – u2 = 2as
We get,
(0) 2 – (25)2 = 2 (-2.5) (S’)
625 = 5(S’)
S’ = 125 m
Question 14. A space craft flying in a straight course with velocity of 75 km s-1 fires its rocket motors for 6.0 s. At the end of this time its speed is 120 km s-1 in the same direction.
Find:
(i) The space craft’s average acceleration while the motors were firing
(ii) The distance travelled by the space craft in the first 10 s after the rocket motors were started, the motors being in action for only 6 s.
Answer:
Given, the initial velocity u = 75 km/s
Final velocity v = 120 km/s
Time taken = 6 s
(i) Acceleration = (Final velocity – Initial velocity)/time taken
= [(120 – 75)/6] kms-2
and = (45/6) kms-2
hence = 7.5 kms-2
(ii) Distance travelled by the aircraft in the first 10 s = Distance travelled in the first 6 s + Distance travelled in the next 4 s.
Distance travelled in the first 6s (S1) = ut + (1/2) at2
(S1) = ut + (1/2) at2
(S1) = (75)(6) + (1/2) (7.5)(6)2
(S1) = 450 + 135
(S1) = 585 km
Distance travelled in the next 4 s (S2) = Speed × time
Speed at the end of 6 s is 120 km/s.
(S2) = (120) (4)
(S2) = 480 km
Thus, the distance travelled by the aircraft in the first 10 s = (S1) + (S2) = 585 + 480 = 1065 km.
(Motion in One Dimension Exe-2C Numericals Class-9 ICSE)
Question 15. A train starts from rest and accelerates uniformly at a rate of 2 m s-2 for 10 s. It then maintains a constant speed for 200 s. The brakes are then applied and the train is uniformly retarded and comes to rest in 50 s. Find
(i) The maximum velocity reached,
(ii) The retardation in the last 50 s,
(iii) The total distance travelled,
(iv) The average velocity of the train.
Answer:
(i) For the first 10 s, initial velocity u = 0
Acceleration a = 2 m/s2
Time taken t = 10 s
Let ‘v’ be the maximum velocity reached.
Using the first equation of motion
v = u + at
We get
V = (0) + (2) (10) = 20 m/s-1
(ii) For the last 50 s: Final velocity = 0 m/s, initial velocity = 20 m/s.
Acceleration = (Final velocity – Initial velocity)/time
= (0 – 20)/50 = -0.4 m/s2
Retardation = 0.4 m/s-2
(iii) Total distance travelled = Distance travelled in the first 10 s + Distance travelled in 200 s + Distance travelled in last 50 s
Distance travelled in first 10s (s1) = ut + (1/2) at2
S1= (0) + (1/2) (2) (10)2
S1= 100 m
Distance travelled in 200s (s2) = speed × time
S2 = (20) (200) = 4000 m
Distance travelled in last 50s (s3) = ut + (1/2) at2
Here, u = 20 m/s, t = 50 s and a = -0.4 m/s2
S3= (20)(50) + (1/2) (-0.4) (50)2
S3= 1000 – 500
S3= 500 m
Therefore, total distance travelled = S1 + S2 + S3 = 100 + 4000 + 500 = 4600 m
(iv) Average velocity = Total distance travelled/total time taken
= (4600/260) m/s
= 17.69 m/s-1
— : End of Motion in One Dimension Exe-2C Equations of Motion Numericals Type Solutions :–
Return to Concise Selina Physics ICSE Class-9 Solutions
Thanks
Please share with your friends
