Newton Laws Numerical on Connected Motion Class-11 Nootan ISC Physics Ch-6 Step by step solutions of Kumar and Mittal Physics of Nageen Prakashan as council latest prescribe guideline for upcoming exam. Visit official Website CISCE for detail information about ISC Board Class-11 Physics.
Newton Laws Numerical on Connected Motion
Class-11 ISC Nootan Ch-6 Solutions of Kumar and Mittal Physics of Nageen Prakashan
| Board | ISC |
| Class | 11 |
| Subject | Physics |
| Writer | Kumar and Mittal |
| Publication | Nageen Prakashan |
| Chapter-6 | Newton Laws of Motion |
| Topics | Numericals based on Connected Motion |
| Academic Session | 2024-2025 |
Numericals based on Connected Motion
Ch-6 Newton Laws of Motion ISC Class-11 Nootan Solutions of Kumar and Mittal Physics of Nageen Prakashan
Question-5: A boy pulls a toy having two carriages placed on a frictionless table by applying a force of 1.5 newton at 30° in a vertical plane. Calculate
(i) the acceleration of the 40 g carriage,
(ii) the acceleration of the 20 g carriage and
(iii) the tension in the string fastened between the two carriages. Show in the figure the forces acting on both separately.

Answer- Now the components of Force are :
Vertical: 1.5 sin 30 = 1.5/2 = 7.5 N
Horizontal: 1.5 cos 30 = 1.5 x √3/2 = 0.75√3 N
Acceleration for 20 gm will be:
Total mass will be: 0.04 kg +0.02 kg = 0.06 kg
a = F/m = 0.75√3 N/ 0.06 kg
a = 21.65 m/s²
Now acceleration for 40 gm will be:
A = √(0.75√3/0.06)²+ (0.75 -0.4/ 0.04)²
After solving, we get:
A = 23.34 m/s²
Then the Tension will be :
T = ma = 0.02 x 21.65 = 0.43 N
=> So the acceleration of the 40 g carriage is 23.34 m/s² acceleration of the 20 g carriage is 21.65 m/s² and the tension in string fastened between two carriages is 0.43 N.
Question-6: In the given figure, three blocks are connected by strings. Masses of blocks are m, 3m and 5m respectively and they are pulled by a force F on a frictionless horizontal surface. The tension P in the first string is 16 N. Calculate: (i) acceleration of blocks, (ii) tension Q in the second string, (iii) force F.
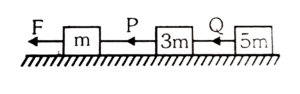
Answer- The total mass of the system is
m = m1+m2+m3 = m + 3m kg + 5m kg = 9m kg
As per given conditions;
F1= (m2+m3)x a;
16 = (8m)a
a = 16/8m
a = 2/m m/s²
(value of m has not been defined as per question statement)
Now; calculating F2;
F2 = m3 x a; = 5m x 2/m;
F2 = 10N
Now calculating F;
Total force = m x a;
Mass have been calculated above;
F = 9m x 2/m, F = 18 N
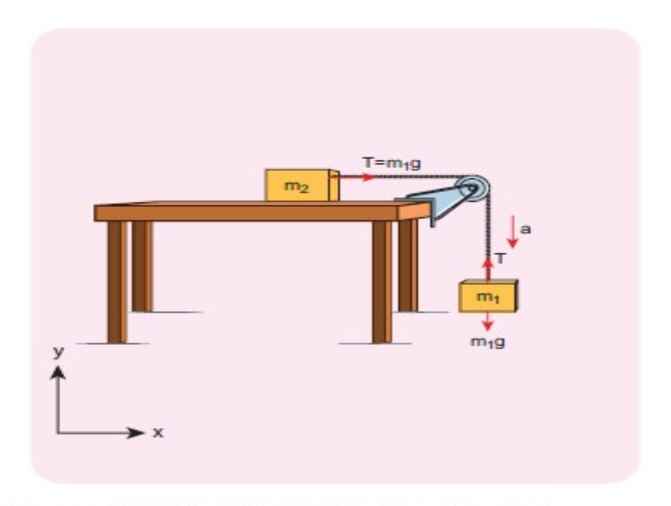
Question-7: Determine, in the given diagram, the acceleration of the system and the tensions T₁ and T₂ in the strings. Assume that the table and the pulleys are frictionless and the strings are massless (g = 9.8 m/s²).

Answer-
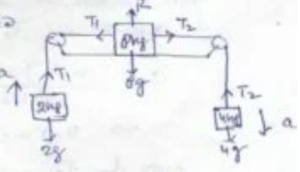
8g will balance R
now,
4g – T2 = 4a
T1 – 2g = 2a
T2 – T1 = 8a
—————–
2 g = 14 a
a = 1.4 m/s²
again, 4 x 9.8 – T2 = 4 x 1.4
T2 = 33.6 N
T1 = 2 x 1.4 + 2 x 9.8
T1 =22.4 N
Question-8: The figure shows a massless, frictionless pulley hanging by a spring-balance. The free ends of a cord passing over the pulley carry 1 kg and 5 kg weights which move under the action of gravity. Will the spring- balance read 6 kg-wt or less than 6 kg-wt or more than 6 kg-wt during the motion of the weights?
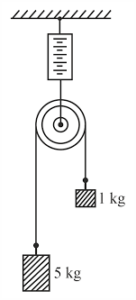
Answer-
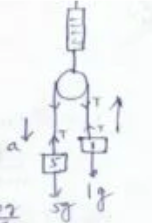
5g -T = 5a
T – g = a
—————–
4g = 6a
a= 4g /6
∴ T = g + a = 4g/6 + g = 10g/6
∴ reading of spring = 2T = 20g/6
which is less than 6g (total suspended weight)
Question-9: Two blocks of masses 10 g and 30 g are fastened to the ends of a cord which passes over a frictionless pulley. The 10 g block rests on the table.
What minimum force must be applied on the 10 g block to keep it on the table ?
What will be the tension in the cord under this condition?
What will be the acceleration of the system and the tension in the cord when the force is withdrawn?
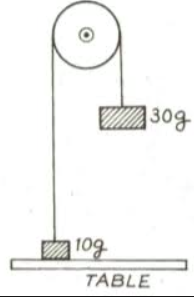
Answer- For two blocks of masses fastened to the ends of a cord which passes over a frictionless pulley we have as per Newton’s Second law :
motion for 30g or 0.03 kg mass will be, 0.03 g – T = 0.03 a ——-(1)
motion for 10g or 0.01 kg mass will be, T – 0.01 g = 0.01 a ——-(2)
Now the answer for the third part of the question can be obtained by solving (1) & (2) and putting g = 9.8 m/s²
a = 4.9 m/s² and T = 0.147 N
for the first and second part of the question the eq (2) has to be modified as under to accommodate minimum force, t, say to be
applied. ‘t’ will be applied downward to keep the 0.01kg mass from rising up. Also now the system will be at rest and so a = 0
The equations will be now as under:
0.03 g T = 0.03 x0 = 0 ———(3)
T 0.01 g t = 0.01×0 = 0 ——–(4)
solving (3) & (4) we get,
t= min force to be applied = 0.196 N
T = tension = 0.294 N
Question-10: Two blocks are connected by a string as shown in the figure. The upper block is hung by another string.
(i) What will be the tension in the upper string due to the two blocks suspended in rest position?
(ii) What force F will have to be applied on the upper string to produce an acceleration of 2 m/s² in the upward direction in both blocks?
(iii) Then, what will be the tension in the string between the two blocks

Answer-10
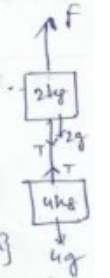
(i) when the system is in rest
F = (4 + 2) g = 6 x 9.8 = 58.8 N
(ii) in case of acceleration 2 m/s² (upward)
=> F – 58.8 N = (2 + 4) x 2
=> F = 58.8 + 12
{F -mg = ma}
=> F = 70.8 N
(iii) for tension in string
T – 4g = 4a
=> T = 4(g +a) => 4(9.8 + 2)
=> T = 47.2 N
—: end of Newton Laws Numerical on Connected Motion Class-11 Nootan ISC Physics Ch-6 solutions of Kumar and Mittal Physics of Nageen Prakashan :—
Return to : – Nootan Solutions for ISC Physics Class-11 Nageen Prakashan
Thanks
Please Share with your friends if helpful


