Nootan Solutions Isothermal and Adiabatic Processes ISC Class-11 Physics Nageen Prakashan

Nootan Solutions Isothermal and Adiabatic Processes ISC Class-11 Physics Nageen Prakashan Chapter-20. Numericals of latest edition. Step by step Solutions of Kumar and Mittal ISC Physics Part-2 Class-11 Nageen Prakashan Numericals Questions. Visit official Website CISCE for detail information about ISC Board Class-11 Physics.

Nootan Solutions Isothermal and Adiabatic Processes ISC Class-11 Physics Nageen Prakashan

Class:	11
Subject:	Physics Part-2
Chapter	20 Isothermal and Adiabatic Processes

Board	ISC
Writer / Publications	Nootan / Nageen Prakashan / Kumar and Mittal
Topics	Solved Numericals of page 779, 780

Nootan Solutions Isothermal and Adiabatic Processes ISC Class-11 Physics Nageen Prakashan

Adiabatic Processes :-

Adiabatic is a process in which there is no heat flow takes place between the system and the surroundings.
These processes are sudden.
The walls of the container should be adiabatic
For an adiabatic process of an ideal gas
From Boyle’s law
PV ^γ = constant

Where γ = C_p/C_v Specific heat ratio

Example: – Hot tea in Thermos flask. It will remain hot as there is no exchange of heat takes place because the walls of thermos is insulating.

Adiabatic change of an ideal gas :-

It implies how much work is done during adiabatic change of an ideal gas.
Initially ideal gas is at Pressure P₁, Volume V₁and Temperature T₁ (P₁,V₁,T₁)
Final state of an ideal gas Pressure P₂,Volume V₂ and Temperature T₂ (P₂,V₂,T₂)
P V ^γ = const
γ =Cp/Cv
If an ideal gas undergoes a change in its state adiabatically from (P₁, V₁) to (P₂, V₂)
P₁V₁^γ = P₂V₂^γ
The work done in an adiabatic change of an ideal gas from the

state (P₁, V₁, T₁) to the state (P₂, V₂, T₂).

W =∫ P V dV = P ∫V dV (Integrating between the limits V₂ and V₁)

For Adiabatic Process

P V ^γ = constant This implies P= constant / V ^γ
W = constant ∫dV/ V ^γ
constant [V^γ-1/- γ+1]
constant/1- γ [V₂^{1- γ} – V₁ ^1-γ]
= constant/1- γ[1/ V₂^{1- γ}– 1/ V₁ ^1-γ]
By solving Work done W= R/ (γ-1)(T₂-T₁), where
T₂= final Temperature
T₁=initial temperature
R=Universal gas constant
γ = Specific heat ratio
This is the work done during adiabatic change.
Consider W= R/ (γ-1)(T₂-T₁)

Isothermal Processes :-

Isothermal :- Iso means same and thermal related to temperature. In Isothermal process the temperature remains constant throughout while all other variables change.
Temperature is constant throughout.
For an ideal gas
- PV = nRT where
- n=no. of moles (constant), R = universal gas constant, T =constant for isothermal process.
This implies PV=constant
Pressure and volume are inversely proportional to each other.
Graphically if we plot pressure and volume

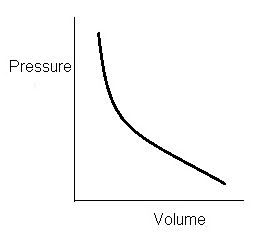
We will get decreasing curve because if we increase pressure volume decreases and vice versa.
This curve is known as Isothermal Curve.

Isothermal Expansion of an Ideal gas :-

It can be described as amount of work done during isothermal expansion of an ideal gas under constant temperature.
Initially ideal gas is at Pressure P₁ and Volume V₁.
At constant temperature the gas will expand from pressure P₁ to P₂ and volume changes from V₁ to V₂.So the final state (P₂,V₂).
These all expansions are QuasiStatic processes.
Consider any intermediate stage ,
- Pressure is P and volume is V₁ + ΔV where ΔV increase in volume.
- ΔW=P ΔV where ΔW = small work done
- By solving and doing calculation the above equation the work done for an ideal gas the work done will be given as :-