Percent and Percentage ICSE Class-8th Concise Selina Mathematics Solutions Chapter-7. We provide step by step Solutions of Exercise / lesson-7 Percent and Percentage for ICSE Class-8 Concise Selina Mathematics. Our Solutions contain all type Questions with Exe-7 A, Exe-7 B and Exe-7 C to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-8.
Percent and Percentage ICSE Class-8th Concise Selina Mathematics Solutions Chapter-7
–: Select Topics :–
Exercise – 7 A Percent and Percentage ICSE Class-8th Concise Selina
Question 1 :-
Evaluate :
(i) 55% of 160 + 24% of 50 – 36% of 150
(ii) 9.3% of 500 – 4.8% of 250 – 2.5% of 240
Answer :-

Question 2 :-
(i) A number is increased from 125 to 150; find the percentage increase.
(ii) A number is decreased from 125 to 100; find the percentage decrease.
Answer :-
New value = 150
Increase
= (150 – 125)
= 25
Increase %
= 25/125 x 100
= 20%
New value = 100,
Decrease
= (125 – 100)
= 25
Decrease %
= 25/125 x 100
= 20%
Question 3 :-
Find :
(i) 45 is what percent of 54?
(ii) 2.7 is what percent of 18?
Answer :-

Question 4 :-
(i) 252 is 35% of a certain number, find the number.
(ii) If 14% of a number is 315; find the number.
Answer :-
By the given condition,
252 = x × 35⁄100
= x×720
∴ x = 252 × 20⁄7
= 36 x 20
= 720
Hence required. number = 720
By the given condition,
315 = x×14⁄100
∴ x = 315×100⁄14
= 45×100⁄2
= 45 x 50
= 2250
Hence required. number = 2250.
Question 5 :-
Find the percentage change, when a number is changed from :
(i) 80 to 100
(ii) 100 to 80
(iii) 6.25 to 7.50
Answer :-
New Number = 100,
Change
= (100 – 80)
= 20
∴ Percentage change (increase)
= 20/80 x 100
= 25%
New number = 80
Change
=(100 – 80)
= 20
∴ Percentage change (decrease)
= 20/100 × 100
= 20%
Original number = 6.25,
New number = 7.50
Change (Increase)
= (7.50 – 6.25)
= 1.25
∴ increase
= 1.25/6.25 x 100
= 20%
Question 6 :-
An auctioneer charges 8% for selling a house. If a house is sold for Rs.2, 30, 500; find the charges of the auctioneer.
Answer :-
Selling price of the house = Rs. 2,30,500
Rate of charges of the auctioneer
= 8% of selling price
∴ Charge of the auctioneer
= 8% of 2,30,500
= 8⁄100 × 2,30,500
= Rs.18,440
Question 7 :-
Out of 800 oranges, 50 are rotten. Find the percentage of good oranges.
Answer :-
Total number of oranges = 800
Rotten oranges = 50
Number of good oranges
= 800 – 50
= 750
Percentage of good oranges
= 750⁄800 × 100
= 750⁄8
= 375/4
= 933⁄4 %
Question 8 :-
A cistern contains 5 thousand litres of water. If 6% water is leaked. Find how many litres of water are left in the cistern.
Answer :-
Water in the cistern = 5000 litres
Quantity of water leaked
= 6⁄100×5000
= 300 litres
Quantity of water left in the cistern
= (5000 – 300) litres
= 4700 litres
Question 9 :-
A man spends 87% of his salary. If he saves Rs.325; find his salary.
Answer :-
Let salary = Rs.x
∴ Expenditure = 87/100 of x
= Rs. 87x/100
Saving = Rs. 325
∴ x-87x/100
= 325
⇒ 100x-87x/100
= 325
⇒ 13x/100
= 325
⇒ x = 325×100/13
⇒ x = 32500/13
⇒ x = 2500
∴ Salary = Rs.2500
Question 10 :-
(i) A number 3.625 is wrongly read as 3.265; find the percentage error.
(ii) A number 5.78 × 103 is wrongly written as 5.87 × 103; find the percentage error
Answer :-
(i)
Correct number = 3.625
Number wrongly read as = 3.265
Error
= 3.625 – 3.265
= 0.360
% Error
= 0.360/3.625 × 100
= 360/3625 × 100
= 36000/3625
= 9.93%
(ii)
Correct number = 5.78 x 103
Number wrongly written as = 5.87 x 103
Error
= 5.87 x 103 – 5.78 x 103
= 0.09 x 103
% Error
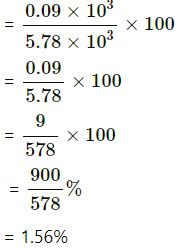
Question 11 :-
In an election between two candidates, one candidate secured 58% of the votes polled and won the election by 18, 336 votes. Find the total number of votes polled and the votes secured by each candidate.
Answer :-
Since, winning candidate secured 58% of the votes polled.
∴ Losing candidate secured
= (100 – 58) of the votes polled
= 42% of the votes polled
Difference of votes
= 58 – 42
= 16% of the votes polled
We are given :
16% of votes polled = 18,336
⇒ 16/100 of the votes polled = 18,336
⇒ Votes polled = 18,336 × 100/16
⇒ Votes polled = 18,33,600/16
⇒ Votes polled = 1,14,600
∴ Votes secured by winning candidate
= 58/100 × 1,14,600
= 66,468
Votes secured by losing candidate
= 42/100 × 1,14,600
= 48,132
Votes polled = 1,14,600
Votes secured by winning candidate = 66,468
Votes secured by losing candidate = 48,132
Question 12 :-
In an election between two candidates, one candidate secured 47% of votes polled and lost the election by 12, 366 votes. Find the total votes polled and die votes secured by the winning candidate.
Answer :-
Since, the losing candidate secured 47% of the votes polled
Winning candidate secures votes
= (100 – 47)% of the votes polled
= 53% of the votes polled
Difference of votes
= 53 – 47
= 6% of the votes polled
We are given :
6% of the votes polled = 12,366
⇒ 6/100 of the votes polled = 12,366
⇒ Votes polled
= 12,366 × 100/6
⇒ = 1236600/6
⇒ = 2,06,100
Votes secured by winning candidate
= 53/100 × 2,06,100
= 1,09,233
∴ Votes polled = 2,06,100
Votes secured by winning candidate = 1,09,233
Question 13 :-
The cost of a scooter depreciates every year by 15% of its value at the beginning of the year. If the present cost of the scooter is
₹ 8,000; find its cost:
(i) after one year
(ii) after 2 years
Answer :-
(i)
Present cost of scooter = Rs.8000
The cost of scooter depreciates by 15% every year
cost of scooter after one year
= (100-15)/100×8000
= 85/100 × 8000
= Rs.6800
(ii)
Present cost of scooter = Rs.8000
The cost of scooter depreciates by 15% every year
Cost of scooter after 2 years
= (100-15)/100 × 6800
= 85/100 × 6800
= Rs.5780
Question 14 :-
In an examination, the pass mark is 40%. If a candidate gets 65 marks and fails by 3 marks; find the maximum marks.
Answer :-
Marks obtained by the candidate = 65
Fails by = 3 marks
Pass marks = 65 + 3 = 68
% of Pass marks = 40%
∴ Required maximum marks
= 100/40 × 68
= 10 x 17
= 170
Question 15 :-
In an examination, a candidate secured 125 marks and failed by 15 marks. If the pass percentage was 35 %; find the maximum marks.
Answer :-
Total marks secured = 125
Failed by 15 marks
∴ Pass marks = 125 + 15
= 140
Let Maximum marks = x
∴ x × 35/100
= 140
⇒ x = 140 × 100/35
= 4 x 100 = 400
Hence maximum marks = 400
Question 16 :-
In an objective type paper of 150 questions; John got 80% correct answers and Mohan got 64% correct answers.
(i) How many correct answers did each get?
(ii) What percent is Mohan’s correct answers to John’s correct answers?
Answer :-
Total questions = 150
John got correct answers = 80%
Mohan got correct answer = 64%
(i) Number of correct answers got by John
= 80/100 × 150
= 120
Number of correct answers got by Mohan
= 64/100 × 150
= 64/4 × 6
= 96
(ii) % of Mohan’s correct answers to John’s correct answers
= 96/120 × 100
= 4/5 × 100
= 4 x 20
= 80%
Question 17 :-
The number 8,000 is first increased by 20% and then decreased by 20%. Find the resulting number.
Answer :-
The resulting number
= The original number x (1+20/100) × (1-20/100)
= 8000 × 120/100 × 80/100
= 7,680
Question 18 :-
The number 12,000 is first decreased by 25% and then increased by 25%. Find the resulting number.
Answer :-
The resulting = The original number x (1-25/100) × (1+25/100)
= 12000 × 75/100 × 125/100
= 11,250
Question 19 :-
The cost of an article is first increased by 20% and then decreased by 30%, find the percentage change in the cost of the article.
Answer :-
Let the original cost = ₹100
Increased by 20%
∴ New cost = 100 + 20 = ₹120
Decreased by 30% = 120×30/100 = ₹36
∴ New cost = 120 – 36 = ₹84
Overall change = 100 – 84 = ₹ 16
Required percentage = 16/100 × 100 = 16% decrease
Question 20 :-
The cost of an article is first decreased by 25% and then further decreased by 40%. Find the percentage change in the cost of the article.
Answer :-
Let the original cost = ₹100
Decreased by 25%
∴ New cost = 100 – 25 = ₹75
Decreased by 40%
= 75 × 40/100 = ₹30
∴ New cost = ₹75 – 30 = ₹45
Overall change = 100 – 45 = ₹55
Required percentage
= 55/100 × 100
= 55% decrease
Exercise – 7 B Solved Questions of Percent and Percentage for ICSE Class-8th Concise Selina Publications
Question 1 :-
A man bought a certain number of oranges ; out of which 13 percent were found rotten. He gave 75% of the remaining in charity and still has 522 oranges left. Find how many had he bought?
Answer :-
Suppose number of oranges bought = 100
Number of Rotten oranges
= 13/100 × 100
= 13
Remaining oranges = 87
Oranges given in charity
= 75/100 × 87
= 3 × 87/4
= 261/4
Net balance of oranges
= 87 – 261/4
= 348 – 261/4
= 87/4
If the balance is 87/4 then number of oranges bought = 100
If the balance is 1 then number of oranges bought = 100×4/87
if the balance is 522 then number of oranges bought
= 100×4/87×522
= 100×4×522/87
= 100 x 4 x 6
= 2400
Question 2 :-
5% pupil in a town died due to some diseases and 3% of the remaining left the town. If 2, 76, 450 pupil are still in the town; find the original number of pupil in the town.
Answer :-
Let original number of pupil in the town = 100
Number of pupil did due to disease
= 5/100×100 = 5
Remaining pupil = 100 – 5 = 95
Number of pupil who left the town
= 3/100×95
= 3×95/100
= 57/20
Actual remaining pupil
= 95-57/20
= 1900-57/20
= 1843/20
If the remaining pupil in the town are 1843/20, then original number of pupil = 100
If the remaining pupil in the town is 1, then original number of pupil = 100×20/1843
If the remaining pupil in the town are 276450, the original number of pupil
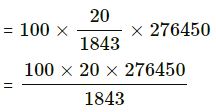
= 100 x 20 x 150
= 3,00,000.
Question 3 :-
In a combined test in English and Physics; 36% candidates failed in English; 28% failed in Physics and 12% in both; find:
(i) the percentage of passed candidates
(ii) the total number of candidates appeared, if 208 candidates have failed.
Answer :-
(i) Candidates failed only in English
= 36% – 12%
= 24%
Candidates failed only in Physics
= 28% – 12%
=16%
Candidates failed in both subjects = 12%
Total failed candidates
= 24% + 16% + 12%
= 52%
Percentage of passed candidates
= 100% – 52%
= 48%
(ii) Candidates failed only in English
= 36% – 12%
= 24%
Candidates failed only in Physics
= 28% – 12%
=16%
Candidates failed in both subjects = 12%
Total failed candidates
= 24% + 16% + 12%
= 52%
If failed candidates are 52, then total candidates appeared = 100
If failed candidates is 1, then total candidates appeared = 100/52
if failed candidates are 208, the total candidates appeared
= 100/52×208
= 100 x 4
= 400
Question 4 :-
In a combined test in Maths and Chemistry; 84% candidates passsed in Maths; 76% in Chemistry and 8% failed in both. Find :
(i) the percentage of failed candidates ;
(ii) if 340 candidates passed in the test ; then how many appeared?
Answer :-
(i) Since, candidates passed in Maths = 84%
∵ candidates failed in Maths
= 100% – 84%
= 16%
Again, candidates passed in Chemistry = 76%
∴ Candidates failed in Chemistry
= 100% – 76%
= 24%
Candidates failed in both = 8%
∴ Candidates failed in only Maths
= 16% – 8%
= 8%
Candidates failed in only Chemistry
= 24% – 8%
= 16%
Total failed candidates
= 8% + 16% + 8%
= 32%
Percentage of failed candidates = 32%
(ii)
Since, candidates passed in Maths = 84%
∵ candidates failed in Maths
= 100% – 84%
= 16%
Again, candidates passed in Chemistry = 76%
∴ Candidates failed in Chemistry
= 100% – 76%
= 24%
Candidates failed in both = 8%
∴ Candidates failed in only Maths
= 16% – 8%
= 8%
Candidates failed in only Chemistry
= 24% – 8%
= 16%
Total failed candidates
= 8% + 16% + 8%
= 32%
Passed candidates
= 100% – 32%
= 68%
If passed candidates are 68, then total candidates appeared = 100
If passed candidate is 1 then total candidates appeared = 100/68
If passed candidates are 340 total candidates appeared
= 100/68×340
= 100×340/68
= 500
Question 5 :-
A’s income is 25% more than B’s. Find, B’s income is how much percent less than A’s.
Answer :-
Let B’s income = Rs.100
then A’s income = 100 + 25
= Rs.125
Now, difference of income of A and B
= Rs.(125 – 100)
= Rs.25
If A’s income is Rs.125, then B’s income less than A = Rs.25
If A’s income is Rs1, the B’s income less than A
= Rs.25/125
If A’s income is rs.100, then B’s income less than A
= Rs. (25/125×100)
= 1/5×100
= Rs.20
∴ B’s income is less than A’s income = 20%
Question 6 :-
Mona is 20% younger than Neetu. How much percent is Neetu older than Mona?
Answer :-
Let Neetu’s age = 100 years
then Mona’s age
= 100 – 20
= 80 years
Difference of ages
= 100 – 80
= 20 years
If Mona is 80 years, then Neetu is older than Mona by = 20 years
If Mona is 1, year, then Neetu is older tan Mona by = 20/80years
If Mona is 100 years, then Neetu is older than Mona by
= 20/80×100years
= 20×100/80
= 25%
Question 7 :-
If the price of sugar is increased by 25% today; by what percent should it be decreased tomorrow to bring the price back to the original?
Answer :-
Let original price of sugar = rs.100
∴ Price of sugar for today
= Rs.100 + Rs.25
= Rs.125
In order to bring down the price to original
i.e. Rs.100, its price should be decreased by
= Rs.125 – Rs100
= Rs.25
∴ On Rs.125, the price should be decreased by
= Rs.25
On Rs.1, the price should be decreased by
= Rs. 25/125
On Rs.100, the price should be decreased by
= Rs. 25/125×100
= Rs. 1/5×100
= Rs.20
∴ Price should be decreased by 20%
Question 8 :-
A number increased by 15% becomes 391. Find the number.
Answer :-
Let the required number = x
∴ According to the statement,
15% of x + x = 391
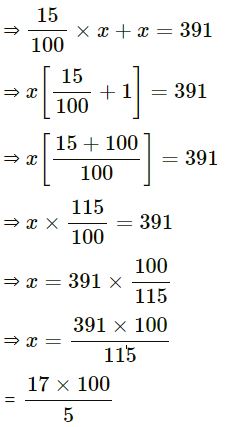
⇒ x = 340
∴ Required number = 340
Question 9 :-
A number decreased by 23 % becomes 539. Find the number.
Answer :-
Let the number = x
According to the statement,
x – 23% of x = 539
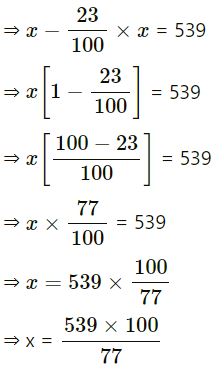
= 7 x 100
⇒ x = 700
∴ Required number = 700
Question 10 :-
Two numbers are respectively 20 percent and 50 percent more than a third number. What percent is the second of the first?
Answer :-
Let the third number = x
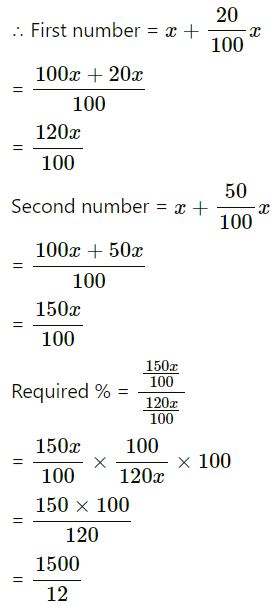
= 125%
Question 11 :-
Two numbers are respectively 20 percent and 50 percent of a third number. What percent is the second of the first?
Answer :-
Let the third number be 100
∴ The first number = 20% of 100
= 20/100×100
= 20
and the second number = 50% of 100
= 50/100×100
= 50
∴ The second no. as the present of the first
= 50/20×100%
= 250%
Question 12 :-
Two numbers are respectively 30 percent and 40 percent less than a third number. What percent is the second of the first?
Answer :-
Let the third number = x
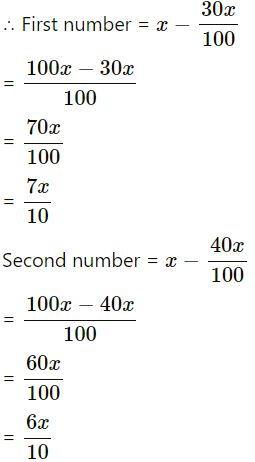

Exercise – 7 C Percent and Percentage for ICSE Class-8th Concise Selina
Question 1 :-
A bag contains 8 red balls, 11 blue balls and 6 green balls. Find the percentage of blue balls in the bag.
Answer :-
Total ball
= 8 + 11 + 6
= 25
Blue balls = 11
∴ Required. percentage
= 11/25×100
= 44%
Question 2 :-
Mohan gets Rs. 1, 350 from Geeta and Rs. 650 from Rohit. Out of the total money that Mohan gets from Geeta and Rohit. what percent does he get from Rohit?
Answer :-
Total money received
= Rs. (1350 + 650)
= Rs. 2000
Amount received from Rohit
= Rs. 650
∴ Required. percentage
= 650/2000×100
= 32.5%
Question 3 :-
The monthly income of a man is Rs. 16, 000. 15 percent of it is paid as income-tax and 75% of the remainder is spent on rent, food, clothing, etc. How much money is still left with the man?
Answer :-
Monthly income = Rs. 16,000
Income tax
= Rs. 16,000×15/100
= Rs.2,400
Remaining
= (16,000 – 2,400)
= Rs. 13,600
Amount spent to rent, food clothing etc.
= 13,600×75/100
= 13,600×3/4
= 3,400 x 3
= Rs. 10,200
Balance left
= 13600 – 10200
= Rs. 3400
Question 4 :-
A number is first increased by 20% and the resulting number is then decreased by 10%. Find the overall change in the number as percent.
Answer :-
Let the original number = 100
Increased by 20%
∴ New number = 100 + 20 = 120
Decreased by 10% = 120×10/100 = 12
∴ New number = 120 – 12 = 108
Overall change = 108 – 100 = 8
Required. Percentage = 8/100×100
= 8% (increase)
Question 5 :-
A number is increased by 10% and the resulting number is again increased by 20%. What is the overall percentage increase in the number?
Answer :-
Let the number be = 100
Increased by 10%
∴ New number = 100 + 10 = 110
Increased by 20%
∴ Net increase = 110×20/100 = 22
∴ New number = 110 + 22 = 132
Overall change = 132 – 100 = 32 (increase)
∴ Increase %
= 32/100×100 = 32%
Question 6 :-
During 2003, the production of a factory decreased by 25%. But, during 2004, it (production) increased by 40% of what it was at the beginning of2004. Calculate the resulting change (increase or decrease) in production during these two years.
Answer :-
Let at the start of 2003, production = 100
decrease = 25%
∴ New production = 100 – 25 = 75
In 2004, it is increased by 40%
∴ Increase = 75×40/100 = 30
∴ New production = 75 + 30 = 105
∴ Resulting change in two years (Increase)
= 105 – 100 = 5
∴ percentage change in increase
= 5/100×100 = 5%
Question 7 :-
Last year, oranges were available at Rs. 24 per dozen ; but this year, they are available at Rs. 50 per score. Find the percentage change in the price of oranges.
Answer :-
Price of 1 orange = 24/12 = Rs.2
New price = 50/20 = Rs.2.50 …[∵ 1 score = 20]
Increase in price = Rs.2.5 – Rs.2.0 = Rs. 0.50
∴ % Change in price (increase)
= 0.50/2 × 100 = 0.50×50 = 25%
Question 8 :-
In an examination, Kavita scored 120 out of 150 in Maths, 136 out of 200 in English and 108 out of 150 in Science. Find her percentage score in each subject and also on the whole (aggregate).
Answer :-
In Maths percentage = 120/150×100
= 4/5xx 100 = 80%
In English percentage
= 136/200×100
= 136/2
= 68%
In Science percentage
= 108/150×100
= 108×2/3
= 72%
Total number scored = 120 + 136 + 108 = 364
Maximum marks = 150 + 200 + 150 = 500
∴ Overall % = 364/500×100 = 364/5 = 72.8%
Question 9 :-
A is 25% older than B. By what percent is B younger than A ?
Answer :-
Alternative Method:
Let age of B = 100 years
∴ Age of A
= 100 + 100 x 25/100
= 125 years
Difference in age by which A is older than B
= 125 – 100
= 25 years
∴ % by which B is younger than A
= 25/125×100
= 20%
Question 10 :-
(i) Increase 180 by 25%.
(ii) Decrease 140 by 18%.
Answer :-
(i)
Increase 180 by 25%
New value
= 180+180×25/100
= 180 + 45
= 225
(ii)
Decrease 140 by 18%
New value
= 140-140×18/100
= 140-14×18/10
= 140-126/5
= 140 – 25.2
= 114.8
Question 11 :-
In an election, three candidates contested and secured 29200, 58800 and 72000 votes. Find the percentage of votes scored by winning candidate.
Answer :-
Total number of votes polled
= 29200 + 58800 + 72000
= 160000
∴ Percentage of votes scored by winning candidate
= 72000/160000×100
= 72×10/16
= 9×10/2
= 45%
Question 12 :-
(i) A number when increased by 23% becomes 861 ; find the number.
(ii) A number when decreased by 16% becomes 798 ; find the number.
Answer :-
(i)
Let the number be x
By the given condition,
x + x × 23/100 = 861
⇒ 100x + 23x /100 = 861
⇒ x(123/100) = 861
⇒ x = 861×100/123 = 7 x 100 = 700
∴ the required number = 700
(ii)
Let the number = 100
By the given condition,
x-x×16100 = 798
⇒ 100x-16x/100 = 798
⇒ 84/100x = 798
⇒ x = 798 × 100/84
= 114 × 100/12
= 114×25/3
= 38 x 25
= 950
∴ The required number = 950
Question 13 :-
The price of sugar is increased by 20%. By what percent must the consumption of sugar be decreased so that the expenditure on sugar may remain the same?
Answer :-
Let price of x kg of sugar = Rs. 100
Increase in price = 20%
∴ New price = 100 + 20 = Rs.120
∴ For Rs. 120, sugar obtained = x kg.
For Rs. 100, sugar obtained
= x/120×100
= 5x/6kg
Original consumption = x kg
New consumption = 5x/6kg
Decrease in consumption
= x – 5x/6
= x 6
Required % decrease in consumption
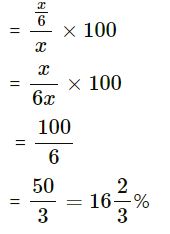
— End of Percent and Percentage Class-8th Solutions :–
Return to – Concise Selina Maths Solutions for ICSE Class -8
Thanks


