ML Aggarwal Percentage and its Applications Exe-7.1 Class 8 ICSE Maths Solutions. We Provide Step by Step Answer of Exe-7.1 Questions for Percentage and its Applications as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-8.
ML Aggarwal Percentage and its Applications Exe-7.1 Class 8 ICSE Maths Solutions
| Board | ICSE |
| Publications | Avichal Publishig Company (APC) |
| Subject | Maths |
| Class | 8th |
| Chapter-7 | Percentage and its Applications |
| Writer | ML Aggarwal |
| Book Name | Understanding |
| Topics | Solution of Exe-7.1 Questions |
| Edition | 2023-2024 |
Percentage and its Applications Exe-7.1
ML Aggarwal Class 8 ICSE Maths Solutions
Page-113
Question 1. Express the following percentages as fractions:
(i) 356%
(ii) 2 ½%
(iii) 16 2/2 %
Answer:
(i) 356%
= 356/100
= 89/25
= 3 14/25
(ii) 2 ½%
= 5/2%
= 5/ (2 × 100)
= 1/40
(iii) 16 2/3 %
= 50/3 %
= 50/3 × 1/100
= 1/6
Question 2. Express the following fractions as percentages:
(i) 3/2
(ii) 9/20
(iii) 1 ¼
Answer:
(i) 3/2
= 3/2 × 100%
= 150%
(ii) 9/20
= 9/20 × 100%
= 45%
(iii) 1 ¼
= 5/4 × 100%
= 125%
Question 3. Express the following fractions as decimals. Then express the decimals as percentages:
(i) ¾
(ii) 5/8
(iii) 3/16
Answer:
(i) ¾ = 0.75
¾ = ¾ × 100%
= 3 × 25%
= 75%
(ii) 5/8 = 0.625
5/8 = 5/8 × 100%
= 5/2 × 25%
= 125/2%
= 62.5%
(iii) 3/16 = 0.1875
3/16 = 3/16 × 100%
= ¾ × 25%
= 75/4%
= 18.75%
Question 4. Express the following fractions as decimals correct to four decimal places. Then express the decimals as percentages:
(i) 2/3
(ii) 5/6
(iii) 4/7
Answer:
(i) 2/3 = 0.6667
2/3 = 0.6667 × 100% = 66.67%
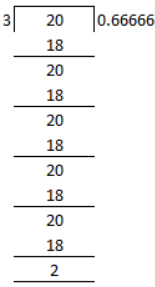
(ii) 5/6 = 0.8333
5/6 = 0.8333 × 100% = 83.33%
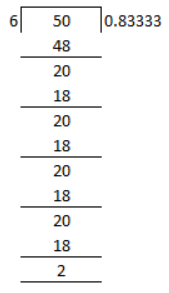
(iii) 4/7 = 0.5714
4/7 = 0.5714 × 100% = 57.14%
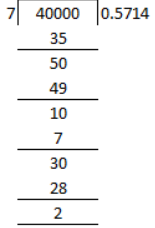
Question 5. Express the following ratios as percentages:
(i) 17: 20
(ii) 13: 18
(iii) 93: 80
Answer:
(i) 17: 20
17: 20 = 17/ 20
= 17/20 × 100%
= 17 × 5%
= 85%
(ii) 13: 18
13: 18 = 13/18
= 13/18 × 100%
= 13/9 × 50%
= 650/9 %
= 72 2/9%
(iii) 93: 80
93: 80 = 93/80
= 93/80 × 100%
= 93/4 × 5%
= 465/4%
= 116.25 %
Question 6. Express the following percentages as decimals:
(i) 20%
(ii) 2%
(iii) 3 ¼ %
Answer:
(i) 20%
= 20/100
= 0.20
= 0.2
(ii) 2%
= 2/100
= 0.02
(iii) 3 ¼
= 13/4
Multiply the denominator by 100
= 13/ (4 × 100)
= 13/ 400
= 3.25/100
= 0.325
Question 7. Find the value of:
(i) 27 % of ₹ 50
(ii) 6 ¼ % of 25 kg
Answer:
(i) 27 % of ₹ 50
= 27/100 of ₹50
= 27/100 × 50
= 27/2
= ₹ 13.50
(ii) 6 ¼ % of 25 kg
= 25/4% of 25 kg
= 25/ (4 × 100) of 25 kg
= (25 × 25)/ (4 × 100)
= 25/16
= 1 9/16 kg
Question 8. What percent is:
(i) 300 g of 2 kg
(ii) ₹ 7.50 of ₹ 6
Answer:
(i) Required percentage = [300 gram/ 2 kg × 100] %
= [300 gram/ (2 × 1000 gram) × 100] %
= [300/ (2 × 1000) × 100] %
= (30/2) %
= 15 %
(ii) Required percentage = [₹ 7.50/ ₹ 6 × 100] %
= [7.50/ 6 × 100] %
= [7.50/3 × 50] %
= [2.50 × 50] %
= 125%
Question 9. What percent of:
(i) 50 kg is 65 kg
(ii) ₹ 9 is ₹ 4
Answer:
(i) Consider x% of 50 kg as 65 kg
x% of 50 kg = 65 kg
x/ 100 × 50 = 65
x/ 2 = 65
x = 130
Therefore 130% of 50 kg is 65 kg.
(ii) Consider x% of ₹ 9 is ₹ 4
x% of ₹ 9 = ₹ 4
x/ 100 × 9 = 4
x = 4 × 100/9
x = 400/9
x = 44 4/9
Therefore, 44 4/9 % of ₹ 9 is ₹ 4
Question 10.
(i) If 16 2/3 % of a number is 25, find the number.
(ii) If 13.25 % of a number is 159, find the number.
Answer:
(i) Consider the number as x
16 2/3 % of x = 25
50/3 % of x = 25
50/3 × 1/100 of x = 25
x = (25 × 3 × 100)/ 50
x = 150
Therefore, the number is 150.
(ii) Consider the number as x
13.25% of x = 159
13.25/ 100 of x = 159
x = (159 × 100)/ 13.25
Multiply and divide by 100
x = (159 × 100 × 100)/ 1325
x = (159 × 4 × 100)/ 53
x = 3 × 4 × 100
x = 1200
Therefore, the number is 1200.
Question 11.
(i) Increase the number 60 by 30 %
(ii) Decrease the number 750 by 10%
Answer:
(i) New number = (1 + 30/100) of 60
= (1 + 3/10) × 60
= 13/10 × 60
= 78
(ii) New number = (1 – 10/100) of 750
= (1 – 1/10) × 750
= 9/10 × 750
= 9 × 75
= 675
Question 12.
(i) What number when increased by 15% becomes 299?
(ii) On decreasing the number by 18%, it becomes 697. Find the number.
Answer:
(i) Consider the original number as x
New number = (1 + 15/100) of original number
299 = (1 + 3/20) × x
Taking LCM
299 = [(20 + 3)/ 20] × x
299 = 23/20 × x
x = (299 × 20)/ 23
x = 13 × 20
x = 260
Therefore, the original number is 260.
(ii) Consider the original number as x
New number = (1 – 18/100) of original number
697 = (1 – 18/100) of x
Taking LCM
697 = [(100 – 18)/ 100] × x
697 = 82/100 × x
x = (697 × 100)/ 82
x = (697 × 50)/ 41
x = 17 × 50
x = 850
Therefore, the original number is 850
Question 13. Mr. Khanna spent 83% of his salary and saved ₹ 1870. Calculate his monthly salary.
Answer:
Mr. Khanna spent 83% of his salary
Savings = 100 – 83 = 17%
So 17% of his salary = ₹ 1870
His salary = ₹ (1870 × 100)/ 17
= ₹ 11000
Question 14. In school, 38% of the students are girls. If the number of boys is 1023, find the total strength of the school.
Answer:
No. of girls in school = 38%
No. of boys in school = (100 – 38) % = 62%
Consider x as the total strength of school
62% of x = 1023
62/100 × x = 1023
x = 1023 × 100/62
x = 1023 × 50/31
x = 33 × 50
x = 1650
Therefore, the total strength of the school is 1650.
Percentage and its Applications Exe-7.1
ML Aggarwal Class 8 ICSE Maths Solutions
Page-114
Question 15. The price of an article increases from ₹ 960 to ₹ 1080. Find the percentage increase in the price.
Answer:
Increase in the price of an article = 1080 – 960 = ₹ 120
Percentage increase in the price = 120/960 × 100%
= 1/8 × 100%
= 100/8 %
= 25/2 %
= 12.5 %
Question 16. In a straight contest, the loser polled 42% votes and lost by 14400 votes. Find the total number of votes polled. If the total number of eligible voters was 1 lakh, find what percentage of voters did not vote.
Answer:
Losing candidate got 42% of the votes polled
Votes secured by winning candidate = (100 – 42) % of the votes polled
= 58 % of the votes polled
So the difference of votes = 58% – 42%
= 16% of the votes polled
16% of the votes polled = 14400
16%/100 of the votes polled = 14400
So the votes polled = 14400 × 100/16
= 900 × 100
= 90000
Total number of eligible voters = 100000
No. of voters who did not vote = 100000 – 90000
= 10000
Percentage of voters did not vote = [10000/ 100000 × 100] %
= 10000/1000 %
= 10 %
Question 17. Out of 8000 candidates, 60% were boys. If 80% of the boys and 90% of the girls passed the exam, find the number of candidates who failed.
Answer:
Total number of candidates = 8000
No. of boys = 60% of 8000
= 60/100 × 8000
= 60 × 80
= 4800
No. of girls = 8000 – 4800 = 3200
No. of passed boys = 80% of No. of boys
= 80/100 × 4800
= 80 × 48
= 3840
No. of passed girls = 90% of No. of girls
= 90/100 × 3200
= 90 × 32
= 2880
No. of passed candidates = 3840 + 2880 = 6720
No. of failed candidates = 8000 – 6720 = 1280
Hence, the number of candidates who failed is 1280.
Question 18. On increasing the price of an article by 16%, it becomes ₹ 1479. What was its original price?
Answer:
Consider the original price of an article = ₹ x
1479 = (1 + 16/100) of original price
1479 = [(100 + 16)/ 100] × ₹ x
1479 = 116/100 × x
116x/100 = 1479
By separating the terms
x = (1479 × 100)/ 116
x = (1479 × 25)/ 29
x = 51 × 25
x = 1275
Hence, the original price of an article is ₹ 1275.
Question 19. Pratibha reduced her weight by 15%. If now she weighs 59.5 kg, what was her earlier weight?
Answer:
Weight reduced by Pratibha = 15%
Present weight of Pratibha = 59.5 kg
Consider her original weight = 100
Reduced weight = 100 – 15 = 85%
85% of her original weight = 59.5 kg
So her original weight = (59.5 × 100)/ 85
= 0.7 × 100
= 70 kg
Question 20. In a sale, a shop reduces all its prices by 15%. Calculate:
(i) the cost of an article which was originally priced at ₹ 40.
(ii) the original price of an article which was sold for ₹ 20.40.
Answer:
Rate of reduction = 15%
(i) Original price of an article = ₹ 40
Rate of reduction = 15%
Reduction = (40 × 15)/ 100 = ₹ 6
So the sale price = 40 – 6 = ₹ 34
(ii) Sale price = ₹ 20.40
Rate of reduction = 15%
Cost price = (SP × 100)/ (100 – reduction %)
= (20.40 × 100)/ (100 – 15)
= (2040 × 100)/ (100 × 85)
= ₹ 24
Question 21. Increase the price of ₹ 200 by 10% and then decrease the new price by 10%. Is the final price same as the original one?
Answer:
Rate of increase = 10%
Rate of decrease = 10%
Price of article = ₹ 200
Increased price = ₹ 200 × (100 + 10)/ 100
= ₹ 200 × 110/100
= ₹ 220
Decreased price = ₹ 200 × (100 – 10)/ 100
= ₹ 220 × 90/100
= ₹ 198
No, the final price is not as same as the original one.
Question 22. Chandani purchased some parrots. 20% flew away and 5% died. Of the remaining, 45% were sold. Now 33 parrots remain. How many parrots had Chandani purchased?
Answer:
Consider Chandani purchased x parrots
No. of parrots flew away = 20% of x
= 20/100 × x
= 1/5 × x
= x/5
No. of parrots died = 5% of x
= 5/100 × x
= x/20
No. of parrots remaining = x – (x/5 + x/20)
Taking LCM
= x – [(4x + x)/ 20]
= x – 5x/20
= x – x/4
Taking LCM
= (4x – x)/ 4
= 3x/4
No. of sold parrots = 45% of 3x/4
= 45/100 × 3x/4
= 9/20 × 3x/4
= 27x/80
No. of parrots which are not sold = 3x/4 – 27/80
Taking LCM
= (60x – 27x)/ 80
= 33x/80
33x/80 = 33
By cross multiplication
33x = 33 × 80
x = (33 × 80)/ 33
x = 80
hence, Chandani purchased 80 parrots.
Question 23. A candidate who gets 36% marks in an examination fails by 24 marks but another candidate, who gets 43% marks, gets 18 more marks than the minimum pass marks. Find the maximum marks and the percentage of pass marks.
Answer:
Consider x as the maximum marks
Marks secured by the first candidate = 36% of x
= 36/100 × x
= 36x/ 100
Marks secured by another candidate = 43% of x
= 43/100 × x
= 43x/ 100
The qualifying marks are same for both the candidates
36x/100 + 24 = 43x/100 – 18
24 + 18 = 43x/100 – 36x/ 100
Taking LCM
42 = (43x – 36x)/ 100
42 = 7x/100
x = 42 × 100/7
x = 6 × 100
x = 600
Here the maximum marks = 600
Marks secured by first candidate = 36/100 × 600 = 36 × 6 = 216
Qualifying marks = 216 + 24 = 240
So the percentage of qualifying marks = (240/600 × 100) %
= 240/6 %
= 40 %
therefore, the maximum mark is 600 and the percentage of pass marks is 40%.
Question 24. The side of rectangle are 20 cm and 15 cm. If each side is increased by 20 %, find the percentage increase in the area.
Answer:
Length of rectangle is 20cm
Breadth is 15cm
Area of rectangle is length *breadth
Area is 20*15 = 300cm².
A1= 300 cm²
If the length and breadth are increased by 20percent
Then length = 20+ 20*0.20= 24cm
Breath = 15+15*0.20= 18Cm.
Area is 24*18 =432cm²
A2= 432cm²
Difference between two areas is = 432–300
132cm²
Percentage of area increased is (132/300)*100
Is 44% Ans
Question 25. Imran gives 1 % of his monthly income to his two sons as pocket money. The elder son gets 80 % of the total amount given and he spends 80 % of his share. If he saves 60 Rs. per month determine imrans’s monthly income.
Answer:
Let, Imran’s monthly income be x
Pocket money given to the two sons = x/100
Money given to the elder son = (80/100 x x/100)
Savings on his share = (100-80)% = 20%
ATP
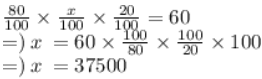
Imran’s monthly income is ₹37500.
— : End of ML Aggarwal Percentage and its Applications Exe-7.1 Class 8 ICSE Maths Solutions :–
Return to – ML Aggarwal Maths Solutions for ICSE Class -8
Thanks
Please Share with Your Friends


