Perimeter and Area of Plane Figures ICSE Class-6th Concise Selina Maths

Perimeter and Area of Plane Figures ICSE Class-6th Concise Selina Mathematics Solutions Chapter-32. We provide step by step Solutions of Exercise / lesson-32 The Perimeter and Area of Plane Figures for ICSE Class-6 Concise Selina Mathematics.

Our Solutions contain all type Questions of Exe-32 A and Exe-32 B with Notes on “Perimeter and Area of Plane Figures” to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-6 Mathematics.

Perimeter and Area of Plane Figures ICSE Class-6th Concise Selina Mathematics Solutions Chapter-32

---

–: Select Topics :–

 Notes 

Exe-32 A,

 Exe-32 B,

---

Notes 

1. Perimeter: It is the length of the boundary of the given figure.
(i) Perimeter of a triangle = Sum of its three sides.
(ii) Perimeter of rectangle = 2 (length + breadth)
(iii) Perimeter of square = 4 x side.

2. Area: Area is the measure of surface of the plane covered by a closed plane figure. In other words, we can say that area of a closed plane figure is the measure of its interior region.

(i) Area of rectangle = length x breadth
(ii) Area of square = (side)².

3. Units of measurement of perimeter and area :
(i) Perimeter is measured in centimetre (cm) metre (m) or millimetre (mm).
(ii) Area is measured in square mm, square cm or square metre.

---

 Exercise – 32 (A) Perimeter and Area of Plane Figures for ICSE Class-6th Concise Selina Mathematics 

Question -1.

What do you understand by a plane closed figure?
Answer-1

Any geometrical plane figure bounded by lines (straight or curved) in a plane is called a plane closed figure.
Each of the following figures is a plane closed figure

Question- 2.

The interior of a figure is called region of the figure. Is this statement true ?
Answer-2

Yes. The interior of the figure along with its boundary is called region of the figure

Question- 3.

Answer-3

(i) Required perimeter

= AB + AC + BE + EF + FH + HG + HD
= 15 + 5 + 25 + 10 + 5 + 15 + 25 = 110 cm

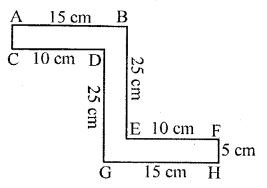
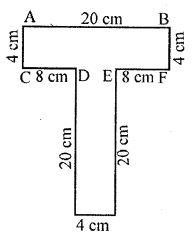
(ii) Required perimeter

= AB + AC + CD + DG + BF + EF + EH + GH
= 20 + 4 + 8 + 20 + 4 + 8 + 20 + 4 = 88 cm

Question -4.

(i) length = 40 cm and breadth = 35 cm
(ii) length = 10 m and breadth = 8 m
(iii) length = 8 m and breadth = 80 cm
(iv) length = 3.6 m and breadth = 2.4 m
Answer-4

(i) length = 40 cm and breadth = 35 cm
∴Perimeter = 2 (length + breadth)
= 2 (40 cm + 35 cm)
= 2 x 75 cm
= 150 cm = ¹⁵⁰⁄₁₀₀
= 1.5 m
(ii) length = 10 m and breadth = 8 m
∴Perimeter = 2 (length + breadth)
= 2 (10 m + 8 m)
= 2 x 18 m = 54 m
(iii) length = 8 m and
breadth = 80 cm
Length = 8 m
Breadth = 80 cm= ⁸⁰⁄₁₀₀ m = 0.8 m
∴ Perimeter = 2 (length + breadth)
= 2 (8 m + 0.8m)
= 2 x 8.8 m = 17.6 m
(iv) length = 3.6 m and breadth = 2.4 m
∴ Perimeter = 2 (length + breadth)
= 2 (3.6 m + 2.4 m)
= 2 x 6 m = 12 m

Question -5.

(i) l, if P = 38cm and b = 7cm
(ii) b, if P = 3.2m and l = 100 cm
(iii) P, if l = 2 m and b = 75cm
Answer-5

(i)

l, if P = 38cm and b = 7cm

Length, (l) = P⁄₂  -b

=³⁸⁄₂   -7 cm

= 19 cm – 7 cm

= 10 cm

(ii) b, if P = 3.2m and l = 100 cm

b, if P = 3.2m and l = 100 cm

[∴100 cm=100⁄₁₀₀ m= 1m]

Breadth, (b) = P⁄₂-l

=3.2⁄₂m  -1m

= 1.6 m – 1 m = 0.6

(iii) P, if l = 2 m and b = 75cm

[∴100 cm=  75⁄₁₀₀ m= 0.75 m]

P, if l = 2 m and b = 75cm

∴ Perimeter = 2(l + b)

= 2 (2 + 0.75)

= 2 (2.75)

= 5.5 m

Question -6.

Answer-6

∵ Side of the square = 1.6 m

∴ its perimeter = 4 x side

= 4 x 1.6 m

= 6.4 m

Question -7.

Find the side of the square whose perimeter is 5 m.
Answer-7

Perimeter of the square = 5 m

∴ Its side = ^perimeter⁄₄

=⁵⁄₄m

= 1.25 m

Question- 8.

A square field has each side 70 m whereas a rectangular field has length = 50 m and breadth = 40 m. Which of the two fields has greater perimeter and by how much?
Answer-8

Perimeter of the square field = 4 x side = 4 x 70m = 280m

Perimeter of rectangular field = 2 (length + breadth)

= 2 (50 m + 40 m)

= 2 x 90 m

= 180 m

∴Square field has greater perimeter by 280 m – 180 m

= 100 m

Question- 9.

A rectangular field has length = 160m and breadth = 120 m. Find :
(i) the perimeter of the field.
(ii) the length of fence required to enclose the field.
(iii) the cost of fencing the field at the rate of ? 80 per metre.
Answer-9

Given = length = 160 m, breadth = 120m

(i) The Perimeter of the field = 2 (l + b)

= 2 (160 m + 120 m)

= 2 x 280

= 560 m

(ii) The length of fence required to enclose the field = The perimeter of the rectan-gular field = 560 m

(iii) The cost of fencing the field = Length of fence x Rate of fence

= 560 m x ₹80 per metre

= ₹44, 800

Question- 10.

Each side of a square plot of land is 55 m. Find the cost of fencing the plot at the rate of ₹32 per metre.
Answer-10

∵ Perimeter of square field = 4 x its side = 4 x 55 m

∴ Length of required fencing = 220 m Now, the cost of fencing = its length x its rate

= 220 m x ₹ 32 per metre?

= ₹ 7040

Question -11.

Each side of a square field is 70 cm. How much distance will a boy walk in order to make ?
(i) one complete round of this field?
(ii) 8 complete rounds of this field?
Answer-11

(i) Distance covered by the boy to make one complete round of the field.
The perimeter of the field: 4 x its side = 4 x 70 = 280 m

(ii) Distance covered by the boy to make 8 complete rounds of this field.
= 280 m x 8 m = 2240 m

Question- 12.

A school playground is rectangular in shape with length = 120 m and breadth = 90 m. Some school boys run along the boundary of the play-ground and make 15 complete rounds in 45 minutes. How much distance they run during this period.
Answer-12

Length of the rectangular playground = 120 mBreadth of the rectangular playground = 90 m

∴ Perimeter of the rectangular ground = 2(l + b)

= 2(120 + 90) m = 420 m

Thus, in one complete round, boys covers a distance of = 420 m

∴ Distance covered in 15 complete rounds = 420 m x 15 = 6300 m

Question- 13.

Mohit makes 8 full rounds of a rectangular field with length = 120 m and breadth = 75 m.
John makes 10 full rounds of a square field with each side 100 in. Find who covers larger distance and by how much?
Answer-13

Mohit

Length of the rectangular field = 120

Breadth of the rectangular field = 75 m

∴ Distance covered in one round (perimeter)

= 2(1 + b) = 2(120 + 75) = 390 m

Hence, distance covered in 8 rounds = 390 x 8 m = 3120 m

John

Side of the field = 100 m

∴Distance covered in one round = 4 x a = 4 x 100 = 400 m

Hence, Distance covered in 10 rounds = 400 x 10 m = 400 m

John a covers greater distance then Mohit by = (4000-3120) m = 880 m

Question -14.

The length of a rectangle is twice of its breadth. If its perimeter is 60 cm, find its length.
Answer-14

Let the breadth of the field = x cm

∴ its length = 2x

and, its perimeter = 2 x (length + breadth)

= 2 x (2x + x)

= 2(3x)

= 6x cm

Perimeter = 60 cm

⇒ 60 cm = 6x cm

⇒ x =⁶⁰⁄₆ = 10 cm

∴ Breadth = x = 10 cm

Length = 2x = 2 x 10 = 20 cm

Question -15.

Find the perimeter of :
(i) an equilateral triangle of side 9.8 cm.
(ii) an isosceles triangle with each equal side = 13 cm and the third side = 10 cm.
(iii) a regular pentagon of side 8.2 cm.
(iv) a regular hexagon of side 6.5 cm.
Answer-15

(i)

The perimeter of equilateral triangle = 3 x side

= 3 x 9.8 cm

= 29.4 cm

(ii)

Required perimeter = 13 cm + 13 cm + 10 cm = 36 cm

(iii)

Perimeter of given pentagon = 5 x side = 5 x 8.2 cm = 41 cm
(iv)

Perimeter of given hexagon = 6 x side = 6 x 6.5 cm = 39 cm

Question -16.

An equilateral triangle and d square have an equal perimeter. If the side of the triangle is 9.6 cm; what is the length of the side of the square?
Answer-16

Perimeter of equilateral triangle = Perimeter of square Side of triangle = 9.6 cm

∴ Perimeter of triangle = 3 x side

= 3 x 9.6 cm = 28.8 cm

⇒ Perimeter of the square = 28.8 cm

4 x the side of square = 28.8 cm

⇒ The side of the square = ^28.8⁄₄ cm

= 7. 2 cm

Question- 17.

A rectangle with length = 18 cm and breadth = 12 cm has same perimeter as that of a regular pentagon. Find the side of the pentagon.
Answer-17

Length of rectangle = 18 cm

Breadth of rectangle = 12 cm

∴ Perimeter of rectangle = 2 x (l + b)

= 2 x (18+12)

= 2 x 30 = 60 cm

∵ Perimeter, of rectangle = Perimeter of pentagon

60 cm = 5 x side

side = ⁶⁰⁄₅ cm = 12 cm

∴ Side of the pentagon = 12 cm

Question -18.

A regular pentagon of each side 12 cm has same perimeter as that of a regular hexagon. Find the length of each side of the hexagon.
Answer-18

Perimeter of regular pentagon = 5 x length of the side

= 5 x 12 cm = 60 cm

Clearly, perimeter of the given pentagon = 60 cm

⇒ 6 x side of hexagon = 60 cm 60

⇒ side of hexagon = ⁶⁰⁄₆ cm = 10 cm

cm = 10 cm

Question- 19.

Each side of a square is 45 cm and a rectangle has length 50 cm. If the perimeters of both (square and rectangle) are same, find the breadth of the rectangle.
Answer-19

Side of a square = 45 cm

∴ Perimeter = 4a = 4 × 45 cm = 180 cm

or perimeter of rectangle = 180 cm

Length of rectangle = 50 cm

∴ Breadth = ^P⁄₂ -l=¹⁸⁰⁄₂ -50

= 90 – 50 = 40

Question -20.

A wire is bent in the form of an equilateral triangle of each side 20 cm. If the same wire is bent in the form of a square, find the side of the square.
Answer-20

∵ Each side of the given equilateral triangle = 20 cm

∴ Perimeter of the triangle = 3 x side = 3 x 20 cm = 60 cm,

∴ Perimeter of the square = Perimeter of equilateral triangle

⇒ 4 x side of square = 60 cm

⇒ The side of the square =  ⁶⁰⁄₄

= 15 cm

---

Selina Solutions of Perimeter and Area of Plane Figures Exe-32 (B), for ICSE Class-6th Concise Mathematics  

Question -1.

Find the area of a rectangle whose :
(i) length = 15 cm breadth = 6.4 cm
(ii) Length = 8.5 m breadth = 5 m
(iii) Length = 3.6 m breadth = 90 cm

(iv) Length = 24 cm breadth =180 mm

Answer-1

(i)

length = 15 cm breadth = 6.4 cm

⇒ Area of the rectangle = Length × breadth

= 15 cm × 6.4 cm

= 96 cm²

(ii)

length = 8.5 m breadth = 5 m

⇒ Area of the rectangle = Length × breadth

= 8.5 m × 5 m

= 42.5 m²

(iii)

length = 3.6 m breadth = 90 cm

⇒ Area of the rectangle = Length × breadth

= 3.6 m × 0.9 m  …[90cm=⁹⁰⁄₁₀₀ m=0.9m]

= 3.24 m²

(iv)

length = 24 cm breadth =180 mm

⇒ length = 24 cm

breadth =180 mm = ¹⁸⁰⁄₁₀ cm = 18 cm

⇒ Area of the rectangle = Length × breadth

= 24 cm × 18 cm

= 432 cm²

Question -2.

Find the area of a square, whose each side is :
(i) 7.2 cm
(ii) 4.5 m
(iii) 4.1 cm
Answer-2

(i) 7.2 cm

Area of the square = (side)²

= (7.2 cm)²

= 7.2 cm x 7.2 cm

= 51.84 cm²

(ii) 4.5 m

Area of the square = (side)²

= (4.5 m)²

= 4.5 m x 4.5 m

= 20.25 m²

(iii) 4.1 cm

Area of the square = (side)²

= (4.1 cm)²

= 4.1 cm x 4.1 cm

= 16.81 cm²

Question- 3.

If A denotes area of a rectangle, l represents its length and b represents its breadth, find :
(i) l, if A = 48 cm² and b = 6 cm
(ii) b, if A = 88 m² and l = 8m
Answer-3

(i) l, if A = 48 cm² and b = 6 cm

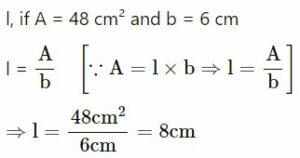
(ii) b, if A = 88 m² and l = 8m

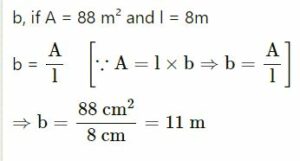
Question- 4.

Each side of a square is 3.6 cm; find its
(i) perimeter
(ii) area.
Answer-4

(i) perimeter

Perimeter = 4 x side

= 4 x 3.6 cm

= 14.4 cm

(ii) area.

Area = (side)²

= (3.6 cm)²

= 12.96 cm²

Question- 5.

The perimeter of a square is 60 m, find :
(i) its each side its area
(ii) its new area obtained on increasing
(iii) each of its sides by 2 m.
Answer-5

Perimeter of a square = 60 m
(i) Perimeter of a square = 4 x side
60 m = 4 x side
⁶⁰⁄₄  = side
∴side = 15 m
(ii) Area of square = (side)² = (15 m)²
= 15 m x 15 m
= 225 m²
(iii) Increased each side = 2 m
Side of square = 15 m
New length of side = (2m + 15m)
= 17m
∴New Area of square = (17m)² = 17m x 17m = 289 m²

Question -6.

Each side of a square is 7 m. If its each side be increased by 3 m, what will be the increase in its area.
Answer-6

Each side of square = 7 m
∴Area of square = (side)²= (7 m)²
= 7m x 7m =49m²
∵ Side increased by 3 m
∴Total length of side will be = 3 m + 7 m = 10m
∴Area of square = (10 m)²= 10m x 10 m = 100 m²
∴Increase in area = 100 m² – 49 m² = 51 m²

Question -7.

The perimeter of a square field is numerically equal to its area. Find each side of the square.
Answer-7

Perimeter of square = Area of square

∵ 4a = a²

⇒a²⁄_a =4

⇒ a = 4

∴ each side of square = 4

Question -8.

A rectangular piece of paper has area = 24 cm² and length = 5 cm. Find its perimeter.
Answer-8

∵ Area of rectangle = length × breadth

⇒ 24 cm² = 5 cm × breadth

⇒ breadth = 24cm²⁄_5cm=4.8 cm

and, perimeter = 2 × (l + b)

= 2 × (5 cm + 4.8 cm)

= 2 × 9.8 cm

= 19.6 cm

Question -9.

Find the perimeter of a rectangle whose area = 2600 m² and breadth = 50 m.
Answer-9:

∵ Area of rectangle = 2600 m²

and breadth = 50 m

⋅ its length = area ⁄_breadth

=2600cm²⁄_50cm=52 cm

⇒ Perimeter of the rectangle

= 2 × (length + breadth)

= 2 × (52 cm + 50 cm)

= 2 × 102 = 204 cm

Question -10.

What will happen to the area of a rectangle, if its length and breadth both are trebled?
Answer-10:

Let the original length of the rectangle = l and its original breadth = b

∴ its original area = length x breadth i.e A = l – b i. e.

Since,

Increased length -=3l

and, increased breadth = 3b

∴ New area = 3l x 3b = 9 x l x b [∵A = l x b]

⇒ Area of the new rectangle = 9 times than area of original rectangle

Question -11.

Length of a rectangle is 30 m and its breadth is 20 m. Find the increase in its area if its length is increased by 10 m and its breadth is doubled.
Answer-11:

Length of a rectangle (l) = 30 m,

Breadth of the rectangle (b) = 20 m

Area of rectangle = l x b

= 30 x 20 = 600 m²

Since, the length its increased by 10 m and breadth is doubled

∴New length (l) = (30 + 10) m = 40 m

and new breadth = (20 x 2) m = 40 m

∴New area = l x b = 40 x 40 m² = 1600 m²

Hence, the increase in the area = (1600 – 600) m²

= 1000 m²

Question -12.

The side of a square field is 16 m. What will be increase in its area, if:
(i) each of its sides is increased by 4 m
(ii) each of its sides is doubled.
Answer-12:

(i) each of its sides is increased by 4 m

Side of a square field (a) = 16 m

∴ Area of a square field = (a)²

= 16 × 16 m² = 256 m²

Each of its sides is increased by 4 m

∴ New side = (16 + 4)m = 20 m

∴ New area of the square field = (a)²

= 20 × 20 m² = 400 m²

(ii) each of its sides is doubled.

Side of a square field (a) = 16 m

∴ Area of a square field = (a)²

= 16 × 16 m² = 256 m²

Each of its side is doubled

∴ New side = (16 × 2)m = 32 m

∴ New area of the square field.. = (a)²

= 32 × 32 m² = 1024 m²

Question- 13.

Each rectangular tile is 40 cm long and 30 cm wide. How many tiles will be required to cover the floor of a room with length = 4.8 m and breadth = 2.4 m.
Answer-13:

Area of each rectangular tiles = 40 cm × 30 cm

= 0.4 m × 0.3 m tiles = 0.12 m²

⇒ Area to be covered by the tiles = 4.8 m × 2.4 m = 15.36 m²

∴ Required number of tiles

= Area to be covered by tiles / Area of each tiles

= …15.36m² ⁄_0.12…= 128.

Question -14.

Each side of a square tile is 60 cm. How many tiles will be required to cover the floor of a hall with length = 50 m and breadth = 36 m.
Answer-14:

Area of each square tile = (side)²

= (60 cm)² = (0.6 m)²

= 0.6 m × 0.6 m = 0.36 m²

And, area to be covered by the tiles = length × breadth

= 50 m × 36 m

= 1800 m²

∴ Required no. of tiles

= Area to be covered by tiles / Area of each tiles

= 1800m² ⁄_0.36m²…= 5000.

Question- 15.

The perimeter of a square plot = 360 m. Find :
(i) its area.
(ii) cost of fencing its boundary at the rate of ₹ 40 per metre.
(iii) cost of levelling the plot at ₹60 per square metre.
Answer-15:

Given, perimeter of square plot = 360 m

∵ Perimeter of the square = 4 x its side

∴ 4 x side of square = 360 m

⇒ side of the square = ³⁶⁰⁄₄ = 90m

(i) The area of the square field = (side)²

= (90 m)²

= 90 m x 90 m

= 8100 m²

(ii) Cost of fencing at ₹ 40 per metre

= 8100 m² x ₹ 40 per metre

= ₹ 324000

(iii) Cost of levelling at₹ 60 per m²

= 8100 m² x ₹60 per m²

= ₹ 486000

Question -16.

The perimeter of a rectangular field is 500 m and its length = 150 m. Find:
(i) its breadth,
(ii) its area.
(iii) cost of ploughing the field at the rate of ₹1.20 per square metre.
Answer-16:

(i) Perimeter of a rectangle = 2 x (length + breadth)

⇒ 500 m = 2 x (150 m + breadth)

⇒ 250 m – 150 m = breadth

∴ breadth = 100 m

(ii) Area of rectangular field = length x breadth

= 150 m x 100 m

= 15000 m²

(iii) Cost of ploughing the field at the rate of

= ₹ 1.20 per square m²= area of the field x rate of ploughing

= 15000 m² x ₹ 1.20 per square metre

= ₹ 15000 x 1.20 = ₹ 18000

Question -17.

The cost of flooring a hall of ₹64 per square metre is ₹2,048. If the breadth of the hall is 5m, find :
(i) its length.
(ii) its perimeter.
(iii) cost of fixing a border of very small width along its boundary at the rate of ₹60 per square metre.
Answer-17:

∵ Total cost of flooring the room = ₹ 2048

and, cost of flooring per square meter = ₹ 64

∴ Area of the room = Total cost of flooringcost of flooring per square meter

=204864 m² = 32 m²

(i) ∵ length × breadth = area

⇒ length × 5 m = 32 m²

⇒ length = 32m25 m = 6.4 m

(ii) Perimeter = 2 × (length + breadth)

= 2 × (6.4 m + 5 m)

= 2 × 11.4 m

= 22.8 m

(iii) Cost of fixing a border at the rate of ₹ 60 per m² = area of hall × rate of fixing

= 32 m² × ₹ 60 per m²

= ₹ 1920

Question- 18.

The length of a rectangle is three times its breadth. If the area of the rectangle is 1875 sq. cm, find its perimeter.
Answer-18

Let the breadth of a rectangle = x

and the length of a rectangle = 3x

∴ Area of the rectangle = l × b

⇒ 1875 cm² = x × 3x

⇒ 3x² = 1875

⇒ x² = ¹⁸⁴⁵⁄₃

⇒ x = √625

⇒ x = 25 cm

∴ Breadth of a rectangle = 25 cm

and length of a rectangle = 3 × 25 cm = 75 cm

Now, perimeter of a rectangle = 2 (l + b)

= 2 (75 + 25) cm

= 2 × 100 cm = 200 cm

–: End of Perimeter and Area of Plane Figures Solutions :–

Return to – Concise Selina Maths Solutions for ICSE Class -6

Thanks