Polygons ICSE Class-6th Concise Selina Mathematics Solutions Chapter-28. We provide step by step Solutions of Exercise / lesson-28 Polygons for ICSE Class-6 Concise Selina Mathematics.
Our Solutions contain all type Questions of Exe-28 A and Exe-28 B with Notes on Polygons to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-6.
Polygons ICSE Class-6th Concise Selina Mathematics Solutions Chapter-28
–: Select Topics :–
What are Polygons?
- A Polygon is a closed figure made up of lines segments (not curves) in two-dimensions.
- A minimum of three line segments are required for making a closed figure, thus a polygon with a minimum of three sides is known as Triangle.
Type of Polygons
Regular Polygon
If all the sides and interior angles of the polygon are equal, then it is known as a regular polygon.
Irregular Polygon
If all the sides and the interior angles of the polygon are of different measure, then it is known as an irregular polygon.
Convex Polygon
If all the interior angles of a polygon are strictly less than 180 degrees, then it is known as a convex polygon. The vertex will point outwards from the centre of the shape.
Concave Polygon
If one or more interior angles of a polygon are more than 180 degrees, then it is known as a concave polygon. A concave polygon can have at least four sides. The vertex points towards inside of the polygon.

Exercise – 28 A Polygons ICSE Class-6th Concise Mathematics Selina Solutions
Question -1.
State, which of the following are polygons :

Answer-1:
Only figure (ii) and (iii) are polygons.
Question- 2.
Find the sum of interior angles of a polygon with :
(i) 9 sides
(ii) 13 sides
(iii) 16 sides
Answer-2:
(i) 9 sides
No. of sides n = 9
∴Sum of interior angles of polygon = (2n – 4) x 90°
= (2 x 9 – 4) x 90°
= 14 x 90°= 1260°
(ii) 13 sides
No. of sides n = 13
∴ Sum of interior angles of polygon = (2n – 4) x 90° = (2 x 13 – 4) x 90° = 1980°
(iii) 16 sides
No. of sides n = 16
∴ Sum of interior angles of polygon = (2n – 4) x 90°
= (2 x 16 – 4) x 90°
= (32 – 4) x 90° = 28 x 90°
= 2520
Question -3.
Find the number of sides of a polygon, if the sum of its interior angles is :
(i) 1440°
(ii) 1620°
Answer-3
(i) 1440°
1440°
Let no. of. sides = n
∴ Sum of interior angles of polygon = 1440°
∴ (2n – 4) × 90° = 1440°
⇒ 2n – 4 = 1440⁄90
⇒ 2(n – 2) = 1440⁄90
⇒ n – 2 = 1440⁄90×2
⇒ n – 2 = 8
⇒ n = 8 + 2
⇒ n = 10
(ii) 1620°
Let no. of sides = n
∴ Sum of angles of polygon = 1620°
∴ (2n – a) × 90° = 1620°
⇒ 2(n – 2) = 1620⁄90
⇒ n – 2 = 1620⁄90×2
⇒ n – 2 = 9
⇒ n = 9 + 2
⇒ n = 11
Question- 4.
Answer-4:
Let no. of. sides be = n
Sum of interior angles of polygon = 1030°
∴ (2n – 4) × 90° = 1030°
⇒ 2(n – 2) = 1030⁄90
⇒ (n – 2) = 1030⁄90×2
⇒ (n – 2) = 103⁄18
⇒ n = 103⁄18+2
⇒ n = 139⁄18
Which is not a whole number. Hence it is not possible to have a polygon, the sum of whose interior angles is 1030°.
Question -5.
(ii) If all the angles of an octagon are equal, find the measure of each angle,
Answer-5:
No. of sides of hexagon, n = 6
Let each angle be = x°
Sum of angles = 6x°
(n – 2) x 180° = Sum of angles
(6 – 2) x 180° = 6x°
4 x 180 = 6x
x = 4×180⁄6
x = 120°
∴ Each angle of hexagon = 120°
(ii) If all the angles of an octagon are equal, find the measure of each angle,
No. of. sides of octagon n = 8
Let each angle be = x°
∴ Sum of angles = 8x°
∴ (2n – 4) × 90° = Sum of angles
(2 × 8 – 4) × 90° = 8x°
12 × 90° = 8x°
⇒ x° =90 x 12⁄8
⇒ x° = 135°
∴ Each angle of octagon = 135°
Question -6.
Answer-6:
Let the angles of a quadrilateral be x°,
x°, x° and 90°
∴ Sum of interior angles of quadrilateral = 360°
⇒ x° + x° + x° + 90° = 360°
⇒ 3x° = 360° – 90°
⇒ x = 270⁄3
⇒ x = 90°
Question -7.
If angles of quadrilateral are in the ratio 4 : 5 : 3 : 6 ; find each angle of the quadrilateral.
Answer-7:
Let the angles of the quadrilateral be 4x, 5x, 3x and 6x.
∴ 4x + 5x + 3x + 6x = 360°
18x = 360°
x = 360⁄18=20°
∴ First angle = 4x = 4 × 20° = 180°
Second angle = 5x = 5 × 20° = 100°
Third angle = 3x = 3 × 20° = 60°
Fourth angle = 6x = 6 × 20° = 120°
Question -8.
Answer-8:
One angle of a pentagon = 120°
Let remaining four angles be x, x, x and x
Their sum = 4x + 120°
But sum of all the interior angles of a pentagon = (2n – 4) x 90°
= (2 x 5 – 4) x 90° = 540°
= 3 x 180° = 540°
∴ 4x+120o° = 540°
4x = 540° – 120°
4x = 420
x = 420⁄4 ⇒ x = 105°
∴Equal angles are 105° (Each)
Question- 9.
The angles of a pentagon are in the ratio 5 : 4 : 5 : 7 : 6 ; find each angle of the pentagon.
Answer-9:
Let the angles of the pentagon be 5x, 4x, 5x, 7x, 6x
Their sum = 5x + 4x + 5x + 7x + 6x = 27x
Sum of interior angles of a polygon
= (2n – 4) × 90°
= (2 × 5 – 4) × 90° = 540°
∴ 27x = 540 ⇒ 540⁄27
⇒ x = 20°
∴ Angles are 5 × 20° = 100°
4 × 20° = 80°
5 × 20° = 100°
7 × 20° = 140°
6 × 20° = 120°
Question- 10.
Two angles of a hexagon are 90° and 110°. If the remaining four angles arc equal, find each equal angle.
Answer-10:
Two angles of a hexagon are 90°, 110°
Let remaining four angles be x, x, x and x
Their sum = 4x + 200°
But sum of all the interior angles of a hexagon
= (2n – 4) × 90°
= (2 × 6 – 4) × 90° = 8 × 90° = 720°
∴ 4x + 200° = 720°
⇒ 4x = 720° – 200° = 520°
⇒ x = 520⁄4=130°
∴ Equal angles are 130° (each)
Polygons Exe-28 B for ICSE Class-6th Concise Selina Mathematics Solved Questions
Question -1.
Fill in the blanks :
In case of regular polygon, with

Answer-1:
| Number of sides | Each exterior angle | Each interior angle |
| (i) 6 | 60° | 120° |
| (ii) 8 | 45° | 135° |
| (iii) 10 | 36° | 144° |
| (iv) 18 | 20° | 160° |
| (v) 8 | 45° | 135° |
| (vi) 24 | 15° | 165° |
(i) Each exterior angle = 360⁄6=60∘
Each interior angle = 180° – 60° = 120°
(ii) Each exterior angle = 360⁄8 = 45°
Each interior angle = 180° – 45° = 135°
(iii) Since each exterior angles = 36°
∴ Number of sides = 360⁄36=10
Also, interior angle = 180°- 20° = 160°
(iv) Since each exterior angles = 20°
∴ Number of sides = 360⁄20=18
Also, interior angle = 180° – 20° = 160°
(v) Since interior angles = 135°
∴ exterior angle = 180° – 135°
∴ Number of sides = 360⁄45°=8
(vi) Since interior angle = 165°
∴ exterior angle = 180° – 165° = 15°
∴ Number of sides = …360⁄15°..= 24…..
Question -2.
Find the number of sides in a regular polygon, if its each interior angle is :
(i) 160°
(ii) 150°
Answer-2:
(i) 160°
Let no.of.sides of regular polygon be n.
Each interior angle = 160°
∴n-2⁄ n×180∘=160∘
180n – 360° = 160n
180n – 160n = 360°
20n = 360°
n = 18
(ii) 150°
Let no.of.sides of regular polygon be n.
Each interior angle = 150°

=150∘
180n – 360° = 150n
180n – 150n = 360°
30n = 360°
n = 12
Question -3.
Find number of sides in a regular polygon, if its each exterior angle is :
(i) 30°
(ii) 36°
Answer-3:
(i) 30°
Let number of sides = n
∴360⁄n =30∘
n = 360⁄30∘
n = 12
(ii) 36°
Let no. of. sides = n
∴360⁄n =36°
n = 360⁄36∘
n = 10
Question -4.
Is it possible to have a regular polygon whose each interior angle is :
(i) 135°
(ii) 155°
Answer-4
(i) 135°
No. of. sides = n
Each interior angle = 135°
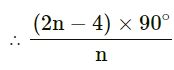
=135∘
180n – 360° = 135n
180n – 135n = 360°
n = 360⁄45∘
n = 8
Which is a whole number.
Hence, it is possible to have a regular polygon whose interior angle is 135°.
(ii) 155°
No. of. sides = n
Each interior angle = 155°
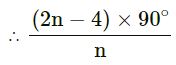
=155∘
180n – 360° = 155n
180n – 155n = 360°
25n = 360°
n = 360⁄25∘
n = 72⁄5∘
Which is not a whole number.
Hence, it is not possible to have a regular polygon whose interior angle is 155°
Question -5.
Is it possible to have a regular polygon whose each exterior angle is :
(i) 100°
(ii) 36°
Answer-5:
(i) 100°
Let no. of. sides = n
Each exterior angle = 100°
= 360⁄n∘=100∘
∴ n = 360⁄100∘
n = 18⁄5
Which is not a whole number.
Hence, it is not possible to have a regular polygon whose each exterior angle is 100°.
(ii) 36°
et no. of. sides = n
Each exterior angle = 36°
= 360⁄n∘=36∘
∴ n = 360⁄36∘
n = 10
Which is a whole number.
Hence, it is not possible to have a regular polygon whose each exterior angle is 36°.
Question- 6.
The ratio between the interior angle and the exterior angle of a regular polygon is 2 : 1. Find :
(i) each exterior angle of this polygon.
(ii) number of sides in the polygon.
Answer-6
(i) each exterior angle of this polygon.
Interior angle : exterior angle = 2 : 1
Let interior angle = 2x° & exterior angle = x°
∴ 2x° + x° = 180°
3x = 180°
x = 60°
∴ Each exterior angle = 60°
(ii) number of sides in the polygon.
Let no.of. sides = n
360⁄n =60°
n = 360⁄60∘
n = 6
–: End of Polygons ICSE Class-6th Concise Solutions :–
Return to – Concise Selina Maths Solutions for ICSE Class -6
Thanks


