Progressive Travelling Waves Numerical Class-11 Nootan ISC Physics Ch-25. Step by step solutions of Kumar and Mittal Physics of Nageen Prakashan as council latest prescribe guideline for upcoming exam. Visit official Website CISCE for detail information about ISC Board Class-11 Physics.
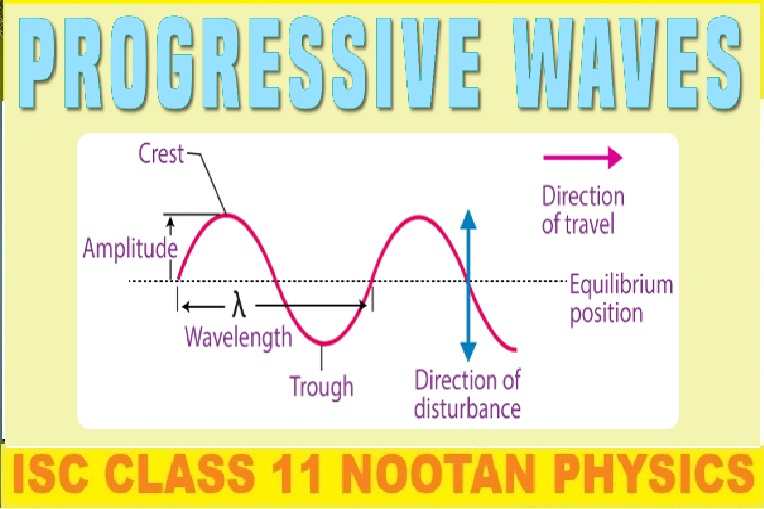
Progressive Travelling Waves Numerical Class-11 Nootan ISC Physics Ch-25
| Board | ISC |
| Class | 11 |
| Subject | Physics |
| Book | Nootan |
| Chapter-25 | Wave |
| Topics | Numericals on Progressive Travelling Waves |
| Academic Session | 2025-2026 |
Numericals on Progressive Travelling Waves
Q-1: The frequency of a radio transmission centre is 30 MHz. Find out the wavelength of the waves transmitted from the station.
Ans- Suppose that the wavelength of wave is λ
we know that
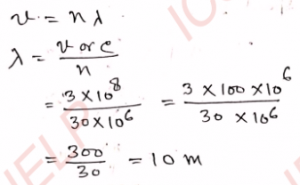
Q-2: Ripples are being generated by a vibrator on the surface of water. The distance between two consecutive crests is 3 cm. Ripples cover a distance of 25.2 cm in 1.2 s. Calculate the wavelength, wave velocity and the frequency of the generated waves.
Ans- Wavelength (λ) = Distance between two consecutive crests = 3.0 cm
Wave velocity (v) = 25.2/1.2 = 21 cm/s
Frequency (n) = v/λ = 21/3 = 7 s^-1
Q-3: A wave of frequency 250 Hz travels with a speed of 4800 m s^-1 in iron. (i) What will be its wavelength in iron ? (ii) What will be its wavelength in air if its speed in air is 332 m s^-1?
Ans- Wavelength of wave in iron
λ = v/n = 4800/250 = 19.2 m
(ii) Wavelength of wave in air = v/n = 332/250 = 1.33 m
Q-4: The wavelength of a wave in a medium is 0.5 m. The phase difference between the oscillations produced at two points in the medium due to this wave is π / 5. Calculate the minimum distance between these two points.
Ans- We know that
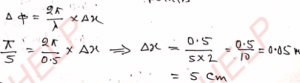
Q-5: The phase difference between the vibrations of two particles in a medium is π / 3. Find the wavelength of the wave if the distance between the particles is 10 cm.
Ans- We know that
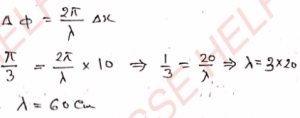
Q-6: The speed of a wave in a string is 20 m s^-1 and its frequency is 50 s^-1. Calculate the phase difference in radian between two points situated at a distance of 10 cm on the string.
Ans-

Q-7: The frequency of a wave propagating in a string is 20 Hz. What will be the difference in the phase of a particle of the string in a time-interval of 0.01 s?
Ans- We know that
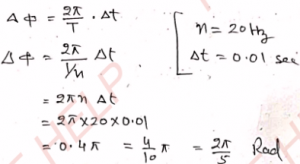
Q-8: Write the equation of a progressive wave propagating along the positive x-direction, whose amplitude is 5 cm, frequency 250 Hz and velocity 500 m s^-1.
Ans- We know that
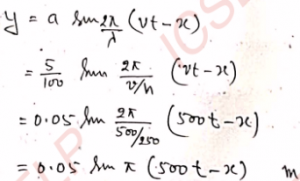
Q-9: A sound-source of frequency 50 hertz is producing longitudinal waves in air. The amplitude of vibration of air-particle is 5 mm and speed of wave 330 m s^-1. Find the distance-displacement equation of the wave.
Ans- Given

Displacement equation

Q-10: A sound-source of frequency 500 hertz is producing longitudinal waves in air. The distance between two consecutive rarefactions in the wave is 0.64 m and the amplitude of oscillation of air particles is 0.002 m. Obtain the displacement equation for this wave.
Ans-
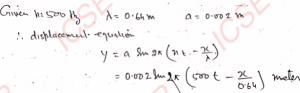
Q-11: A wave of frequency 1000 hertz and amplitude 0.005 m is travelling in a medium with a speed of 300 m s^-1. Write displacement-equation of the oscillations due to this wave at a distance of 0.15 m from the source.
Ans-
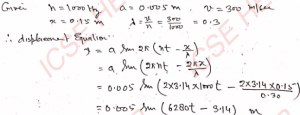
Q-12: The equation of a travelling wave is y = 0.07 sin (12 π x – 500 π t), where the distances are in metre and time t in second. Calculate the wavelength and velocity of the wave.
Ans-

Q-13: The displacement equation of a wave y = 0.5 sin n (2 t – 0.01 x) where x is in metre and t is in second. Find the frequency, amplitude, speed and phase difference between two particles situated at a distance of 5 m from each other.
Ans-

Q-14: The equation for transverse waves in a stretched string is given by y = 0.04 sin π (100 t – 0.005 x) where y and x are in metre and t is in second. State whether the wave is progressive or stationary. What are the amplitude, frequency, wavelength and speed of the wave?
Ans-

Q-15: The displacement-equation of a wave is y = 1.5 sin (6280 t – 12.56 x). Determine the frequency of the wave.
Ans-

Q-16: The equation of motion of a wave is y = 1.2 sin (3.5 t +0.5 x), where distances and time are expressed in metre and second respectively. Determine the velocity and direction of the wave.
Ans-

Q-17: The equation of a wave is y = 0.5 sin π (0.01 x – 3 t); y and x are in metre and t is in second. Calculate the velocity of the wave.
Ans-

Q-18: The displacement equation of a transverse wave in a string is expressed as y = 1.5 sin π (6 t + 0.002 x), where y and x are expressed in cm and t in second. Find (i) speed of the wave, (ii) frequency of the wave. -1
Ans-
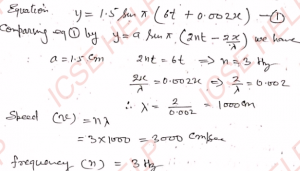
Q-19: A wave whose amplitude is 0.2 mm and frequency is 500 s^-1 travels in air with a velocity of 350 m s^-1. Determine the displacement of the particle situated at a distance of 3.5 m from the origin in the direction of the wave at the instant t = 0.05 s.
Ans-

Q-20: The equation of a wave is y = 5 × 10^-6 sin (800 t – π x / 42.5), where x and y are in cm and t is in second. Find out the amplitude of vibration of the particles of the medium, frequency, wavelength, speed of sound and the phase difference between two particles situated at a distance of 17.0 cm at any instant.
Ans-

Q-21: A progressive wave in a string is expressed by the equation y = 0.4 sin (120 π t – 4 π x / 5) , where the distances are given in metre and time in second. Calculate (i) frequency, (ii) wavelength.
Ans-
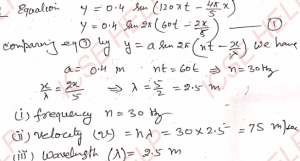
Q-22: The equation of a transverse wave in a string is y = 1.2 sin (6t + 0.005 x) π, where y and x are measured in cm and t in second. (i) Calculate the amplitude, frequency, wavelength and speed of the wave. (ii) Write the equation of that wave whose amplitude and frequency are same but whose phase difference from the above wave is + π/2.
Ans-

Q-23: The equation of motion of a particle is y = 1.2 sin (3.5 t + 0.5x), where distances and time are respectively in metre and second. Determine the amplitude, frequency and maximum velocity of the particle.
Ans-

— : End of Progressive Travelling Waves Numerical Class-11 Nootan ISC Physics Ch-25 :–
Return to : – – Nootan Solutions for ISC Physics Class-11
Thanks
Please share with your friends