Properties of Triangle Class 11 OP Malhotra Exe-7A ISC Maths Solutions Ch-7 Solutions. In this article you would learn about The Law of Sines and Cosines and Area of triangle. Step by step solutions of latest textbook has been given as latest syllabus. Visit official Website CISCE for detail information about ISC Board Class-11 Mathematics.

Properties of Triangle Class 11 OP Malhotra Exe-7A ISC Maths Solutions Ch-7
| Board | ISC |
| Publications | S Chand |
| Subject | Maths |
| Class | 11th |
| Chapter-7 | Properties of Triangle |
| Writer | OP Malhotra |
| Exe-7(A) | The Law of Sines and Cosines and Area of triangle. |
Exercise- 7A
Properties of Triangle Class 11 OP Malhotra Exe-7A Solution.
Que-1: In ∆ABC,
(i) If a = 2, b = 3, c = 4, prove that cos A = 7/8.
(ii) if the sides are 7, 4√3 and √13 cm, prove that the smallest angle is 30°.
(iii) if a = 9, b = 8, c = 4, prove that 6 cos C = 4 + 3 cos B.
(iv) The sines of the angles of a triangle are in the ratio of 4 : 5 : 6 ; prove that the cosines of the angles are 12 : 9 : 2.
(v) If the two angles of a triangle are 30° and 45° and the included side is (√3 + 1) cm, find the area of the triangle.
(vi) If in a ∆ABC, a = 6, b = 3 and cos (A – B) = 4/5, find its area.
(vii) In a triangle ABC, ∠C = 60° and ∠A = 75°. If D is a point on AC such that the area of the ∆ABAD is √3 times the area of the ∆ABCD, find the ∠ABD.
Sol: (i) Given a = 2, b = 2, c = 4
By cosine formula, we have
cos A = (b²+c²−a²)/2bc
= (3²+4²−2²)/(2×3×4)
= (9+16−4)/24
= 21/24 = 7/8
(ii) Let a = 7 ; b = 4√3; c = √13
Since smallest side has smallest angle opposite to it.
Here a > b > c
cos A = (b²+c²−a²)/2bc
= (4√3²+7²−√13²)/(2×7×4√3)
= (48+49−13)/56√3
= 84/56√3
= 3/2√3 = √3/2
C = π/6 or 30°
(iii) Given a = 9, b = 8, c = 4
By using cosine’s formula, we have
cos B = (b²+c²−a²)/2bc
= (9²+4²−8²)/(2×9×4)
= (81+16−64)/72
= 33/72 = 11/24
and cos C = (b²+c²−a²)/2bc
= (9²+8²−4²)/(2×9×8)
= (81+64−16)/144
= 129/144 = 43/48
LHS = 6 cos C
= 6 × (43/48) = 43/8 ………. (1)
RHS = 4 + 3 cos B
= 4 + 3 (11/24) …………… (2)
= 43/8
∴ from eqn. (1) and eqn. (2); we have
6 cos C = 4 + 3 cos B
(iv) Using sine formula, we have
sinA/a = sinB/b = sinC/c … (1)
Since sin A : sin B : sin C = 4 : 5 : 6
Thus using eqn. (1); we have
a = 4k; b = 5k; c = 6k
cos A = (b²+c²−a²)/2bc
= (5k²+6k²−4k²)/(2×5k×6k)
= (61k²-16k²)/60k²
= 45k²/60k² = 3/4
cos B = (b²+c²−a²)/2ac
= (6k²+4k²−5k²)/(2×6k×4k)
= (52k²-25k²)/48k²
= 27k²/48k² = 9/16
cos C = (b²+c²−a²)/2ab
= (4k²+5k²−6k²)/(2×5k×4k)
= (41k²-36k²)/40k²
= 5k²/40k² = 1/8
Cos A : cos B : cos C = 3/4 : 9/16 : 1/8
Cos A : cos B : cos C = 12 : 9 : 2.
(v) Since the sum of angles of ∆ABC is 180°.
∴ ∠A + ∠B + ∠C = 180°
⇒ ∠A + 30° + 45° = 180°
⇒ ∠A = 180° – 75° = 105°
Using sine formula, we have
a/Sin A = b/Sin B = c/Sin C
(√3+1)/sin 105° = b/sin 30° = c/sin 45°
(√3+1)/sin 105° = b/(1/2) = c/(1/√2)
b = (√3+1)/2sin 105° = (√3+1)/2sin (60°+45°) = (√3+1)/2[sin 60° cos 45° + cos 60° sin 45°]
b = (√3+1)/2[(√3/2) (1/√2) + (1/2) (1/√2)]
= {(√3+1) 2√2}/2(√3+1)
= √2
area of ΔABC = 1/2 ab sin C
= (1/2) (√3+1) √2 sin 45°
= (1/2) (√3+1) √2 (1/√2)
= (1/2) (√3+1)
(vi) Given a = 6, b = 3 and cos (A – B) = 4/5
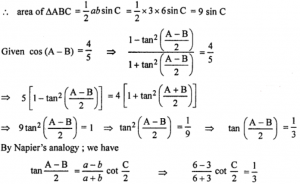
cot C/2 = 1 = 45°
cot C = 90°
(vii) Since the sum of angles of ∆ABC is 180°.
Thus, ∠A = 180°- 75° – 60° = 45°
Let ∠BAD = θ ∴ ∠CBD = 45° – θ
Now, area of ∆BAD = (1/2) x BA x BD sin θ
and area of ∆BCD = (1/2) x BC x BD sin (45° – θ)
according to given condition, we have
1/2 × AD × BE = √3 × (1/2 × CD × BE)
We can cancel 1/2 and BE (assuming BE≠0):
AD = √3 × CD
Let CD = x. Then:
AD = √3x
AC = AD + CD = √3x + x = (√3+1) x
AD/CD = √3/1
This leads to:
cotθ = [1⋅cotA − √3⋅cotC]/√3+1
Where cot A = cot75° and cot C = cot60°.
– cot60° = 1/√3
– cot75° = (√3−1)/(√3+1)
cotθ = [1⋅{(√3−1)/(√3+1)} − {√3⋅(1/√3)}] / √3+1
This simplifies to:
cotθ = {√3−1−1}/{√3+1}
= (√3−2)/(√3+1)
Using the exterior angle property:
∠ADB = 105°
Thus:
∠ABD = ∠ADB − ∠A
= 105°−75° = 30°
In any ∆ABC, Prove that
Que-2: sin A/sin(A+B) = a/c
Sol: Using the formulae we have,
sin A/a = sin B /b = sin C /c = k (say)
a/c = sin A/sin C = sin A/sin (180°-A+C)
sin A/sin(A+B) = a/c
Que-3: a−b/a+b = {tan(1/2)(A−B)}/{tan(1/2)(A+B)}
Sol: Using the formulae we have,
sin A/a = sin B /b = sin C /c = k (say)
a = k sin A ; b = k sin B
LHS = (a-b)/(a+b)
(k sin A – k sin B)/(k sin A + k sin B)
[2 cos {(A+B)/2} sin {(A-B)/2}] / [2 sin {(A+B)/2} cos {(A-B)/2}]
tan {(A+B)/2} cot {(A-B)/2}
Que-4: ac cos B – bc cos A = a² – b²
Sol: LHS = ac cos B – bc cos A
ac [{a²+c²-b²}/2ac] – bc [{b²+c²-a²}/2bc]
{a²+c²-b²-b²-c²+a²}/2
{2(a²-b²)}/2
a² – b² = RHS.
Que-5: {sin(A−C)}/{sin(A+B)} = (a²−b²)/c²
Sol: Using the formulae we have,
sin A/a = sin B /b = sin C /c = k (say)
a = k sin A ; b = k sin B and c = k sin C
RHS = (a²−b²)/c²
[k²(sin²A-sin²B)]/k² sin²C
{sin (A+B) sin (A-B)} / {sin (π-A+B)}²
{sin (A+B) sin (A-B)} / {sin² (A+B)}
sin (A-B) / sin (A+B) = RHS.
Que-6: a (sin B – sin C) + b (sin C – sin A) + c (sin A – sin B) = 0
Sol: Using the formulae we have,
sin A/a = sin B /b = sin C /c = k (say)
Then sin A = ak; sin B = bk and sin C = ck
L.H.S = a (sin B – sin C) + b (sin C – sin A) + c (sin A – sin B)
= a (bk – ck) + b (ck – ak) + c (ak – bk)
= k[ab – ac + bc – ba + ca – bc] = k x 0
= 0 = R.H.S.
Que-7: a cos (A + B + C) – b cos (B + A) – c cos (A + C) = 0
Sol: L.H.S. = a cos (A + B + C) – b cos (B + A) – c cos (A + C)
= a cos π – b cos (π – C) – c cos (π – B)
= – a – b (- cos C) – c (- cos B)
= – a + b cos C + c cos B
= – a + a = 0 = R.H.S.
[using projection formula, b cos C + c cos B = a]
Que-8: a (cos C – cos B) = 2 (b – c) cos² (1/2) A
Sol: Consider
a (cos C − cos B)
= k(sin A cos C − sin A cos B) [∵a/sin A = b/sin B = c/sin C = k]
= k/2 (2sin A cos C − 2sin A cos B)
= k/2 [sin(A+C) + sin(A−C) − sin(A+B) − sin(A−B)]
= k/2 [sin(π−B) + sin(A−C) − sin(π−C) − sin(A−B)] (∵A+B+C = π)
= k/2 [sin B − sin C + sin (A−C) − sin(A−B)]
= k/2 [2sin((B−C)/2) cos((B+C)/2) + 2sin ((A−C−A+B)/2) cos ((A−C+A−B)/2)]
= k sin ((B−C)/2) [cos((π/2)−(A/2)) + cos{{2A−(π−A)}/2}]
= k sin((B−C)/2) (sin(A/2) + sin(3A/2))
= k sin((B−C)/2) [2sin{((A/2) + (3A/2)/2)} cos{((3A/2) − (A/2)}/2)]
= 2k sin((B−C)/2) sin A cos (A/2)
= 4k sin((B−C)/2) sin (A/2) cos²(A/2) …(1)
Now ,
Consider
2(b−c) cos²(A/2)
= 2k(sin B − sin C) cos²(A/2)
= 2k[2sin((B−C)/2)cos((B+C)/2)] cos²(A/2)
= 4k sin((B−C)/2) cos((π/2)−(A/2)) cos²(A/2)
= 4k sin((B−C)/2) sin (A/2) cos²(A/2)…(2)
From (1) & (2), we get
a (cos C − cos B) = 2(b−c) cos²(A/2)
Hence proved.
Que-9: a sin1/2 (B – C) = (b – c) cos 1/2 A
Sol: RHS = b-c/a
{k sin B – k sin C} / k sin A
[2cos {(B+C)/2} sin {(B-C)/2}] / {2sin (A/2) cos (A/2)}
[2cos {(π-A)/2} sin {(B-C)/2}] / {2sin (A/2) cos (A/2)}
[{sin (A/2)} sin {(B-C)/2}] / {2sin (A/2) cos (A/2)}
[sin {(B-C)/2}] / cos (A/2) = LHS
a sin (1/2) (B-C) = (b-c) cos (A/2)
Que-10: a sin(A/2 + B) = (b + c) sin A/2
Sol: Now, (b + c)/a
{k sin B + k sin C}/k sin A
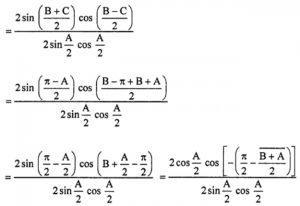
= [sin {(A/2) + B}] / sin (A/2)
a sin(A/2 + B) = (b + c) sin A/2
Que-11: c² = (a – b)² cos² (1/2) C + (a + b)² sin² (1/2) C
Sol: RHS = (a – b)² cos² (1/2) C + (a + b)² sin² (1/2) C
= a²[cos²(C/2) + sin²(C/2)] + b²[cos²(C/2) + sin²(C/2)] – 2ab[cos²(C/2) – sin²(C/2)]
= a² + b² – a² – b² + c²
= c²
= LHS
Hence proved
Que-12: a sin (B – C) + b sin (C – A) + c sin (A – B) = 0
Sol: c² = Using sine formula, we have a/sin A = b/sin B = c/sin C = k ≠ 0 (say)
Then a = k sin A; b – k sin B ; c = k sin C
L.H.S. = a sin (B – C) + b sin (C – A) + c sin (A – B)
= k [sin A sin (B – C) + sin B sin (C-A) + sin C sin (A – B)]
= k [sin (π – B+C) sin(B – C) + sin(π – A+C) sin (C – A) + sin (π – A+B) sin (A – B)] [∵ A + B + C = π]
= k [sin (B + C) sin (B – C) + sin (C + A) sin (C – A) + sin (A + B) sin (A – B)]
= k [sin² B – sin² C + sin² C – sin² A + sin² A – sin² B]
= k x 0 = 0 = R.H.S.
Que-13: {cos2A/a²} − {cos2B/b²} = (1/a²) − (1/b²)
Sol: L.H.S = {cos2A/a²} − {cos2B/b²} = (1−2sin²A)/a² − (1−2sin²B)/b²
Using sine formula, sin A/a = sin B/b = sin C/c = k ≠ 0 (say)
Then sin A = a k; sin B = b k; sin C = c k
= {(1−2a²k²)/a²} − {(1−2b²k²)/b²}
= (1/a²) − 2k² − (1/b²) + 2k²
= (1/a²) − (1/b²) = R.H.S
Que-14: [1+cos(A−B)cos C]/[1+cos(A−C)cos B] = (a²+b²)/(a²+c²)
Sol: LHS = [1+cos(A−B)cos C]/[1+cos(A−C)cos B]
= [1+cos(A−B)cos (π-A+B)]/[1+cos(A−C)cos (π-A+C)]
![Que-14: [1+cos(A−B)cos C]/[1+cos(A−C)cos B] = (a²+b²)/(a²+c²)](https://icsehelp.com/wp-content/uploads/2025/06/b-300x250.png)
Que-15: (b² – c²) cot A + (c² – a²) cot B + (a² – b²) cot C = 0
Sol: Now, LHS = (b² – c²)cotA + (c² – a²)cotB + (a² – b²)cotC
Putting the values of cotA , cotB and cotC
= (1/2abc) P[ (b² – c²)(b² + c² – a²) + (c² – a²)(c² + a² – b²) + (a² – b²)(a² + b² – c²)]
= (1/2abc) P [ b⁴ – c⁴ -a²b² + a²c² + c⁴ – a⁴ -b²c² + b²a² + a⁴ – b⁴ – c²a² + c²b² ]
= (1/2abc) P × 0 = RHS
Que-16: a³ sin (B – C) cosec² A + b³ sin (C – A) cosec² B + c³ sin (A – B) cosec² C = 0
Sol: L.H.S = a³ sin (B – C) cosec² A + b³ sin (C – A) cosec² B + c³ sin (A – B) cosec² C
= (a³/sin²A) sin(B−C) + (b³/sin²B) sin(C−A) + (c³/sin²C) sin(A−B)
[using sine formula, a/sin A = b/sin B = c/sin C = k ≠ 0]
= [k³ sin A sin (B – C) + k³ sin B sin (C – A) + k³ sin C sin (A – B)]
= k³ [sin (π – B+C) sin (B – C) + sin (π – A+C) sin (C – A) + sin (π – A+B) sin (A – B)]
= k³ [sin (B + C) sin (B – C) + sin (A + C) sin (C-A) + sin (A + B) sin (A – B)] [∵ A + B + C = π]
= k³ [sin² B – sin² C + sin² C – sin² A + sin² A – sin² B] = k³ x 0 = 0 = R.H.S.
Que-17: a³ cos (B – C) + b³ cos (C – A) + c³ cos (A – B) = 3abc.
Sol: L.H.S. = a³ cos (B – C) + b³ cos (C – A) + c³ cos (A – B)
= a² [k sin A cos (B – C)] + b² [k sin B cos (C – A)] + c² [k sin C cos (A – B)] [Using sine formula, sin A/a = sin B/b = sin C/c = 1/k]
= ka² sin (π – B+C) cos (B – C) + kb² sin (π – A+C) cos (C – A) + kc² sin (π – A+B) cos (A – B)
= ka² sin (B + C) cos (B – C) + kb² sin (C + A) cos (C – A) + kc² sin (A + B) cos (A – B)
= (ka²/2) (sin 2B + sin 2C) + (1/2)kb² (sin 2C + sin 2A) + (1/2)kc² (sin 2A + sin 2B)
= (ka²/2) [2 sin B cos B + 2 sin C cos C] + (kb²/2) [2 sin C cos C + 2 sin A cos A] + (kc²/2) [2 sin A cos A + 2 sin B cos B]
= a² (b cos B + c cos C) + b² (c cos C + a cos A) + c² (a cos A + b cos B) [using sine formula]
= ab (a cos B + b cos A) + be (b cos C + c cos B) + ac (a cos C + c cos A)
= abc + bca + acb = 3abc = R.H.S. [using projection formulae]
Que-18: (i) In a ∆ABC, if 2cosA/a + cosB/b + 2cosC/c = (a/bc) + (b/ca), prove that ∠A = 90°
(ii) In a ∆ABC, AD is the altitude from A. Given b > c, ∠C = 23° and AD = abc/(b²−c²), find ∠B.
Sol: (i) In ΔABC by cosine rule, we get
cos A = (b²+c²-a²)/2bc, cos B = (a²+c²-b²)/2ac, cos C = (a²+b²-c²)/2ab
2cosA/a + cosB/b + 2cosC/c = (a/bc) + (b/ca) …….[Given]
∴ {2(b²+c-a²)/2abc} + {(a²+c²-b²)/2abc} + [{2(a²+b²-c²)}/2abc] = (2a²+2b²)/2abc
∴ 2b2 + 2c2 – 2a2 + a2 + c2 – b2 + 2a2 + 2b2 – 2c2 = 2a2 + 2b2
∴ b2 – a2 + c2 = 0
∴ a2 = b2 + c2
Hence, ΔABC is a right angled triangle.
(ii) Given ∠B = 23° and AD = abc/(b²−c²) … (1)
Also from right angled ∆ADC, ADAC = sin 23°
⇒ AD = b sin 23° … (2)
∴ from eqn. (1) and eqn. (2); we have

= B-C = 90°
= B = 90° + 23° = 113°
Thus ∠B = 113°
Que-19: In ∆ABC, (a²+b²)/(a²−b²) = {sin(A+B)}/{sin(A−B)}, Prove the triangle is isosceles or right triangle.
Sol: Given : (a²+b²)/(a²−b²) = {sin(A+B)}/{sin(A−B)}
Applying Componendo and Dividendo,
{sin(A-B) + sin(A+B)}/{sin(A-B) – sin(A+B)} = {a²−b²+a²+b²}/{a²−b²-a²−b²}
– {2 sin A cos B}/{2cos A sin B} = 1a²/-2b²
{sin A cos B}/{cos A sin B} = a²/b²
⇒ b² sin A cos B = a² cos A sin B
Putting sin A = ka, sin B = kb
⇒ b²ka cos B = a²kb cos A
⇒ b cos B = a cos A
Applying cosine formula,
b[(a²+c²-b²)/2ac] = a[(b²+c²-b²)/2bc]
⇒ b² (a² + c² – b² ) = a² (b² + c² – a²)
⇒ a²b² + b²c² – b^4 = a²b² + a²c² – a^4
⇒ b²c² – a²c² – b^4 + a^4 = 0
⇒ c² (b² – a²) – (b² – a² ) (b² + a² ) = 0
⇒ (b² – a²) (c² – b² – a² ) = 0
⇒ Either b² – a² = 0
or, c² – b² – a² = 0
⇒ b = a
or, c² = b² + a²
∴ Triangle is isosceles if b = a
∴ Triangle is right angled if c² = b² + a²
Que-20: If sin A / sin C = {sin(A−B)}/{sin(B−C)}, prove that a², b², c² are in A.P.
Sol: By sine rule,
sin A/a = sin B/b = sin C/c = k
∴ sin A = ka, sin B = kb, sin C = kc
Now, sin A/sin C = {sin(A – B)}/{sin(B – C)}
∴ sin A . sin (B – C) = sin C. sin (A – B)
∴ sin [π – (B + C)]. sin (B – C)
= sin [π – (A + B)]. sin(A – B) …..[∵ A + B + C = π]
∴ sin (B + C). sin (B – C) = sin (A + B). sin (A – B)
∴ sin2B – sin2C = sin2A – sin2B
∴ 2 sin2B = sin2A + sin2C
∴ 2k2b2 = k2a2 + k2c2
∴ 2b2 = a2 + c2
Hence, a2, b2, c2 are in A.P.
Que-21: If sin 2A + sin 2B = sin 2C, prove that A = 90° or B = 90°
Sol: Given : sin 2A + sin 2B = sin 2C
2 sin {(2A+2B)/2} cos {(2A-2B)/2} = 2 sin C cos C
2 sin (A+B) cos (A-B) – 2 sin C cos C = 0
sin (π-C) cos (A-B) – sin C cos C = 0
sin C [cos (A-B) – cos C] = 0
sin C [cos (A-B) – cos (π-A+B)] = 0
sin C [cos (A-B) + cos (A+B)] = 0
sin C [2 cos {(A-B+A+B)/2} cos {(A+B-A+B)/2}] = 0
sin C [2 cos A cos B] = 0
sin C ≠ 0
cos A = 0 or cos B = 0
A = 90° or B = 90°
Que-22: If C = 60°, prove that {1/(a+c)} + {1/(b+c)} = 3/(a+b+c)
Sol: Let {1/(a+c)} + {1/(b+c)} = 3/(a+b+c) be true.
⇒ (b+c+a+c)/{(a+c)(b+c)} = 3/(a+b+c)
⇒ (b + a + 2c) (a + b + c) = 3 (a + c) (b + c)
⇒ a² + b² + 2ab + 3c(a + b) + 2c² = 3ab + 3ac + 3bc + 3c²
⇒ a² + b² – c² = ab
⇒ (a²+b²−c²)/2ab = 1/2
⇒ cos C = 1/2 [using cosine formula]
∴ ∠C = π/3 or 60° which is true
Thus {1/(a+c)} + {1/(b+c)} = 3/(a+b+c)
Que-23: (i) In a ∆ABC the angles A, B, C are in A.P. show that 2 cos (A−C)/2 = (a+c)/√(a²−ac+c²)
(ii) If the angles A, B, C of ∆ABC are in A.P. and b : c = √3 : √2 show that A = 75°.
(iii) If A = 45° and B = 75°, show that a + c√2 = 2b.
Sol: (i) Since angles A, B, C of ∆ABC are in A.P.
∴ 2B = A + C
Since sum of all angles of ∆ABC is 180°.
A+B+C = 180°
3B = 180°
B = 60°
cos B = cos 60°
(a²+c²-b²)/2ab = 1/2
a²+c²-b² = ac
a²+c²-ac = b² ……. (1)
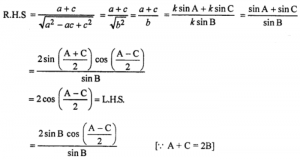
(ii) since A, B, C are the angles of AABC forms A.P.
∴ 2B = A + C … (1)
Also sum of all angles of ∆ABC be 180°.
∴ A + B + C = 180°
⇒ 2B + B = 180°
⇒ B = 60°
given b : c = √3 : √2
⇒ b/c = √3/√2
⇒ sin B / sin C = √3/√2 [using sine formulae]
⇒ sin60°/sin C = √3/√2
⇒ √3/2sin C = √3/√2
⇒ sin C = 1/√2
⇒ C = 45°
∴ A = 2B – C = 2 x 60° – 45° = 120° – 45° = 75
(iii) Since sum of all angles of ∆ABC is 180°.
∴ A + B + C= 180°
⇒ 45° + 75° + C = 180°
⇒ C = 180° – 120° = 60°
L.H.S = a + c√2 = k sin A + √2k sin C [using sine formulae, a/sin A = b/sin B = c/sin C = k]
= k sin 45° + √2k sin 60° = k[(1/√2)+√2×(√3/2)] = k{(1+√3)/√2}
R.H.S = 2b = 2k sin B = 2 k sin 75° = 2k sin (45° + 30°)
= 2k [sin 45° cos 30° + cos 45° sin 30°]
= 2k [(1/√2)+(√3/2)+(1/√2)⋅(1/2)] = k{(√3+1)/√2}
∴ L.H.S = R.H.S
Que-24: The angles A, B, C of a triangle are in the ratio 3:5:4, prove that a + c√2 = 2b
Sol: Since the angles A, B and C of a triangle are in the ratio 3 : 5 : 4.
Let the angles of ∆ABC are, A = 3k; B = 5k; C = 4k
Since the sum of angles of ∆ABC be 180°.
∴ A + B + C = 180°
⇒ 3k+ 5k + 4k = 180°
⇒ 12k = 180° ⇒ k = 15°
∴ A = 3k = 45°; B = 5k = 75° and C = 4k = 60°
∴ LH.S = a + c√2 = k[sin A + √2 sin C] = k [sin 45° + √2 sin 60°]
= k [(1/√2)+√2×(√3/2)] = k((1+√3)/√2)
R.H.S = 2b = 2k sin B = 2k sin 75° = 2k sin (45° + 30°)
= 2k [sin 45° cos 30° + cos 45° sin 30°]
= 2k [(1/√2)×(√3/2)+(1/√2)×(1/2)] = k{(1+√3)/√2}
∴ L.H.S = R.H.S
Que-25: In a ∆ABC, if cos A = 17/22, cos C = 1/14, prove that the ratio of the sides is 7 : 9 :11.
Sol: Given : cos A = 17/22 and cos C = 1/14

Que-26: The angle of a triangle are in the ratio 1:2:7, prove that the ratio of the greatest side to the least side is (√5+1) : (√5−1).
Sol: Since the angles of triangle are given to be in the ratio 1 : 2 : 7.
Let A = x; B = 2x and C = 7x
since the sum of the angles of AABC is 180°.
A + B + C = 180° ⇒ x + 2x + 7x = 180° ⇒ 10x = 180° ⇒ x = 18°
∴ A = 18° ; B = 2 x 18° = 36° and C = 7 x 18°= 126°
Thus greatest side : least side = sin 126° : sin 18°
= sin (180° – 54°): sin 18° = sin 54° : sin 18°
= sin (90° – 36°): sin 18° – cos 36°: sin 18°
= (√5+1)/4 : (√5−1)/4 i.e. √5+1 : √5−1
Que-27: If the sides of ∆ABC are in the ratio 4 : 5 : 6, prove that one angle it twice that of the other.
Sol: Since the sides of AABC are in the ratio 4 : 5 : 6
Let BC = 4k; AC = 5k; AB = 6k
Using cosine formula, we have

cos 2A = cos C
2A = C
Hence one angle of ∆ABC is twice the other.
Que-28: Two sides and included angles of a triangle are respectively 3 + √3, 3 – √3 and 60°. Show that the remaining elements of the triangle are 105°, 15°, 3√2.
Sol: Let a = BC ; b = CA = 3 – √3; c = AB = 3 + √3 and ∠A = 60°
By sine rule,
sin A/a = sin B/b = sin C/c

sin C = sin (60°+45°) = sin 105°
C = 105°
Que-29: In a ∆ABC, if B = 3C, prove that
(i) cos C = √{(b+c)/4c}
(ii) sin A/2 = (b−c)/2c.
Sol: (i) Given B = 3C
Using sine formula,
a/sin A = b/sin B = c/sin C = k ≠ 0 (say)
⇒ a = k sin A; b = k sin B and c = k sin C
Now (b+c)/4c
= (k sin B + k sin C)/4k sin C
= (sin 3C + sin C)/4 sin C
[2 sin {(3C+C)/2} cos {(3C-C)/2}] / 4 sin C
(2 sin 2C cos C)/4sin C
(4 sin C cos² C)/ 4 sin C = cos² C
cos C = √{(b+c)/4c}
(ii) (b-c)/2c = (k sin B – k sin C)/2k sin C
(sin B – sin C)/2 sin C
(sin 3C – sin C)/2 sin C
[2 cos {(3C+C)/2} sin {(3C-C)/2}]/2 sin C
(2 cos 2C sin C)/2 sin C = cos 2C
since the sum of angles of ∆ABC be 180°.
∴ A + B + C = 180°
⇒ A + 3C + C = 180°
⇒ A + 4C = 180°
⇒ 4C = 180° – A
⇒ 2C = (180°−A)/2 = 90° – (A/2)
∴ from (1) ; we have
(b−c)/2c = cos(90°−(A/2))
= sin A/2
–: End Properties of Triangle Class 11 OP Malhotra Exe-7A ISC Math Ch-7 Solution :–
Return to :- OP Malhotra ISC Class-11 S Chand Publication Maths Solutions
Thanks
Please share with your friends