Pythagoras Theorem ICSE Class-7th Concise Selina mathematics Solutions Chapter-16. We provide step by step Solutions of Exercise / lesson-16 Pythagoras Theorem for ICSE Class-7 Concise Selina Mathematics. Our Solutions contain all type Questions of Exe-16 to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-7.
Pythagoras Theorem ICSE Class-7th Concise Selina mathematics Solutions Chapter-16
Exercise – 16
Question 1.
Triangle ABC is right-angled at vertex A. Calculate the length of BC, if AB = 18 cm and AC = 24 cm.
Answer
Given: ∆ ABC right angled at A and AB = 18 cm,
AC = 24 cm.
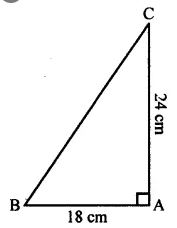
To find: Length of BC.
According to Pythagoras Theorem,
BC2 = AB2 + AC2
= 182 + 242 = 324 + 576
= 900
∴ BC =√900=√30×30
= 30 cm
Question 2.
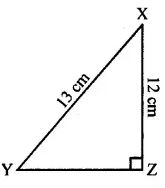
Triangle XYZ is right-angled at vertex Z. Calculate the length of YZ, if XY = 13 cm and XZ = 12 cm.
Answer
Given: ∆XYZ right angled at Z and XY = 13 cm,
XZ = 12 cm.
To find: Length of YZ.
According to Pythagoras Theorem,
XY2 = XZ2 + YZ2
132 = 122 + YZ2
169= 144 +YZ2
169 − 144 = YZ2
25 = YZ2
∴ YZ = √25cm
=√5×5
= 5 cm
Question 3.
Triangle PQR is right-angled at vertex R. Calculate the length of PR, if:
PQ = 34 cm and QR = 33.6 cm.
Answer
Given: ∆PQR right angled at R and PQ = 34 cm,
QR = 33.6 cm.
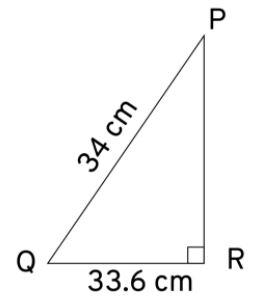
To find: Length of PR.
According to Pythagoras Theorem,
PR2 + QR2 = PQ2
PR2 + 33.62 = 342
PR2+ 1128.96=
1156
PR2 = 1156 − 1128.96
∴ PR = √27.04 =
5.2 cm
Question 4.
The sides of a certain triangle are given below. Find, which of them is right-triangle
(i) 16 cm, 20 cm and 12 cm
(ii) 6 m, 9 m and 13 m
Answer
The given triangle will be a right-angled triangle if square of its largest side is equal to the sum of the squares on the other two sides.
ex, If (20)2 = (16)2
(20)2 = (16)2 + (12)2
400 = 256 + 144
400 = 400
6 m, 9 m, and 13 m
The given triangle will be a right-angled triangle if the square of its largest side is equal to the sum of the squares on the other two sides.
i.e., If (13)2 = (9)2 + (6)2
169 = 81 + 36
= 169 ≠ 117
So, the given triangle is not right-angled.
Question 5.
In the given figure, angle BAC = 90°, AC = 400 m and AB = 300 m. Find the length of BC.

Answer
AC = 400 m
AB = 300 m
BC =?
According to the Pythagoras Theorem,
BC2 = AB2 + AC2
BC2 = (300)2 + (400)2
BC2 = 90000 + 160000
BC2 = 250000
BC = √250000
= 500 m
Question 6.
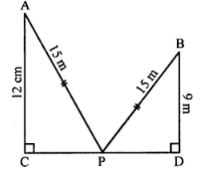
In the given figure, angle ACP = ∠BDP = 90°, AC = 12 m, BD = 9 m and PA= PB = 15 m. Find:
(i) CP
(ii) PD
(iii) CD
Answer
Given :
AC = 12 m
BD = 9 m
PA = PB
= 15 m
(i) In right angle triangle ACP
(AP)2 = (AC)2 + (CP)2
152 = 122 + CP2
225 = 144 + CP2
225 – 144
= CP2
81 = CP
81 = CP
∴ CP = 9 m
(ii) In right angle triangle BPD
(PB)2 = (BD)2 + (PD)2
(15)2 = (9)2 + PD2
225 = 81 + PD2
225 – 81
= PD2
144 = PD2
144 = PD2
∴ PD = 12 m
(iii) CP = 9 m
PD = 12 m
so CD = CP + PD
= 9 + 12
= 21 m
Question 7.
In triangle PQR, angle Q = 90°, find :
(i) PR, if PQ = 8 cm and QR = 6 cm
(ii) PQ, if PR = 34 cm and QR = 30 cm
Answer
(i)
Given:
PQ = 8 cm
QR = 6 cm
PR =?
∠PQR = 90°
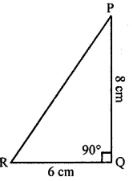
According to the Pythagoras Theorem,
(PR)2 = (PQ)2 + (QR)2
PR2 = 82 + 62
PR2 = 64 + 36
PR2 = 100
∴ PR = 100
= 10 cm
(ii)
Given:
PR = 34 cm
QR = 30 cm
PQ =?
∠PQR = 90°
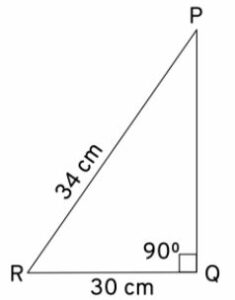
According to the Pythagoras Theorem,
(PR)2 = (PQ)2 + (QR)2
(34)2 = PQ2 + (30)2
1156 = PQ2 + 900
1156 − 900 = PQ2
256 = PQ2
∴ PQ = 256 = 16 cm
Question 8.
Show that the triangle ABC is a right-angled triangle; if:
AB = 9 cm, BC = 40 cm and AC = 41 cm
Answer
CB = 40 cm
AC = 41 cm
AB = 9 cm
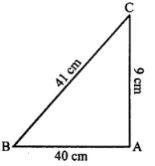
If square of its largest side is equal to the sum of the squares on the other two sides. Then given triangle will be a right-angled triangle
According to Pythagoras Theorem,
(AC)2 = (BC)2 + (AB)2
(41)2 = (40)2 + (9)2
1681 = 1600 + 81
1681 = 1681
Hence,
it is a right-angled triangle ABC.
Question 9.
In the given figure, angle ACB = 90° = angle ACD. If AB = 10 m, BC = 6 cm and AD = 17 cm, find :
(i) AC
(ii) CD

Answer
∆ ABD
∠ACB = ∠ACD = 90°
and AB = 10 cm,
BC = 6 cm,
AD = 17 cm
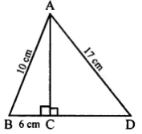
To find:
(i) Length of CD
(ii) Length of AC
Proof:
(i) In right-angle triangle ACD
AD = 17 cm, AC = 8 cm
According to Pythagoras Theorem,
(AD)2 = (AC)2 + (CD)2
(17)2 = (8)2 + (CD)2
289 – 64 = CD2
225 = CD2
CD =15×15
= 15 cm
(ii) In right-angled triangle ABC
BC = 6 cm, AB = 110 cm
According to Pythagoras Theorem,
AB2 = AC2 + BC2
(10)2 = (AC)2 + (6)2
100 = (AC)2 + 36
AC2 = 100 − 36 = 64 cm
AC2 = 64 cm
∴ AC = 8×8
= 8 cm
Question 10.
In the given figure, angle ADB = 90°, AC = AB = 26 cm and BD = DC. If the length of AD = 24 cm; find the length of BC.

Answer
Given:
∆ ABC
∠ADB = 90°,
AC = AB = 26 cm
AD = 24 cm
To find : Length of BC In right angled ∆ ADC
AB = 26 cm,
AD = 24 cm
According to the Pythagoras Theorem,
(AC)2 = (AD)2 + (DC)2
(26)2 = (24)2 + (DC)2
676 = 576 + (DC)2
⇒ (DC)2 = 100
⇒ DC =√100
= 10 cm
∴ Length of BC
= BD + DC
= 10 + 10
= 20 cm
Question 11.
In the given figure, AD = 13 cm, BC = 12 cm, AB = 3 cm and angle ACD = angle ABC = 90°. Find the length of DC.

Answer
Given :
∆ ACD = ∠ABC = 90°
and AD = 13 cm,
BC = 12 cm,
AB = 3 cm
To find : Length of DC.
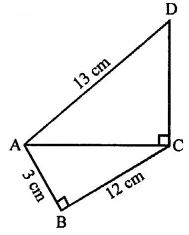
(i) In right angled ∆ ABC
AB = 3 cm, BC = 12 cm
According to Pythagoras Theorem,
(AC)2 = (AB)2 + (BC)2
(AC)2 = (3)2 + (12)2
(AC) =√9+144
=√153 cm
(ii) In right angled ∆ ACD
AD = 13 cm, AC =153
According to Pythagoras Theorem,
DC2 = AB2 − AC2
DC2= 169 − 153
DC = √16
= 4 cm
Question 12.
A ladder, 6.5 m long, rests against a vertical wall. If the foot of the ladder is 2.5 m from the foot of the wall, find up to how much height does the ladder reach?
Answer
Given :
Length of the foot of the wall = 2.5 m
Length of ladder = 6.5 m
To find: Height AC According to Pythagoras Theorem,
(BC)2 = (AB)2 + (AC)2

(6.5)2 = (2.5)2 + (AC)2
42.25 = 6.25 + AC2
AC2 = 42.25 – 6.25
= 36 m
AC = √6×6
= 6 m
∴ Height of wall = 6 m
Question 13.
A boy first goes 5 m due north and then 12 m due east. Find the distance between the initial and the final position of the boy.
Answer
Given: Direction of north = 5 m
ex. AC Direction of east = 12 m
ex. AB
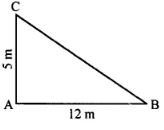
To find: BC
According to Pythagoras Theorem,
In right angled Δ ABC
(BC)2 = (AC)2 + (AB)2
(BC)2 = (5)2 + (12)2
(BC)2 = 25 + 144
(BC)2= 169
∴ BC = √169
=√13×13
= 13 m
Question 14.
Use the information given in the figure to find the length AD.

Answer
Given:
AB = 20 cm
so AO = AB
=202 = 10cm
BC = OD
= 24 cm
Find the :
Length of AD
In right angled triangle
AOD (AD)2 = (AO)2 + (OD)2
(AD)2 = (10)2 + (24)2
(AD)2 = 100 + 576
(AD)2 = 676
∴ AD = √26×26
AD = 26 cm
— End of Pythagoras Theorem ICSE Class-7th Solutions :–
Return to – Concise Selina Maths Solutions for ICSE Class -7
Thanks



Any Class 6 maths and other subjects icse.
ok