Quadratic Equations Class 11 OP Malhotra Exe-10C ISC Maths Solutions

Quadratic Equations Class 11 OP Malhotra Exe-10C ISC Maths Solutions Ch-10 Solutions. In this article you would learn about Nature of roots and Formation of Equations. Step by step solutions of latest textbook has been given as latest syllabus. Visit official Website CISCE for detail information about ISC Board Class-11 Mathematics.

Quadratic Equations Class 11 OP Malhotra Exe-10C ISC Maths Solutions Ch-10

Board	ISC
Publications	S Chand
Subject	Maths
Class	11th
Chapter-10	Quadratic equations
Writer	O.P. Malhotra
Exe-10(C)	Nature of roots and Formation of Equations.

Exercise- 10C

Quadratic Equations Class 11 OP Malhotra Exe-10C Solution.

Que-1: Without solving, find the nature of the roots of the following equations :
(i) 3x² – 7x + 5 = 0.
(ii) 4x² + 4x + 1 = 0.
(iii) 3x² + 7x + 2 = 0.
(iv) x² + px – q² = 0.

Sol: (i) Given quadratic eqn. be 3x² – 7x + 5 = 0
On comparing with ax² + bx + c = 0 ; we have
a = 3; b = – 7; c = 5
Here discriminant D = b² – 4ac
= (- 7)² – 4 x 3 x 5
= 49 – 60 = – 11 < 0
Hence the roots of given quadratic eqn. are imaginary.

(ii) Given quadratic eqn. be 4x² + 4x + 1 = 0
On comparing with ax² + bx + c = 0, we have a = 4; b = 4; c = 1
Here discriminant D = b² – 4ac
= 16 – 4 x 4 x 1 = 0
∴ roots are real and equal.

(iii) Given quadratic eqn. be 3x² + 7x + 2 = 0
On comparing with ax² + bx + c = 0, we have a = 3 ; b = 7 ; c = 2
Here discriminant D = b² – 4ac
= 7² – 4 x 3 x 2
= 49 – 24
= 25 > 0
∴ roots are real, distinct and rational

(iv) Given quadratic eqn. be
x² + px – q² = 0 …(1)
On comparing eqn. (1) with
ax² + bx + c = 0,
we have a = 1 ; b = p ; c = – q²
Here discriminant D = b² – 4ac
= p² – 4 x 1 x (- q²)
= p² + 4q² > 0
Hence the roots are real and unequal if p and q both not equal to 0 and roots are real and equal if p = 0 and q = 0

Que-2: If the equation  (1 + m²) x² + 2mcx + c² – a² = 0 has equal roots, show that c² = a² (1 + m²).

Sol: Given quadratic eqn. be,
(1 + m²)x² + 2mcx + c² – a² = 0 …(1)
On comparing with Ax² + Bx + C = 0
we have, A = 1 + m²; B = 2mc
and C = c² – a²
given eqn. (1) has equal roots.
∴ b² – 4AC = 0
⇒ 4m²c² – 4 (1 + m²) (c² – a²) = 0
⇒ 4m²c² – 4 {c² – a² + m²c² – a²m²} = 0
⇒ – 4 (c² – a² – a²m²) = 0
⇒ c² = a²(1 + m²)

Que-3: Find the value of m so that the roots of the equation (4 – m)x² + (2m + 4) x + (8m + 1) = 0 may be equal.

Sol: Given quadratic equation be,
(4 – m)x² + (2m + 4)x + 8m + 1 = 0
On comparing with ax² + bx + c = 0 ; we have
a = 4 – m ; b = 2m + 4 and c = 8m + 1
Since it is given that roots of eqn. (1) are equal
∴ discriminant = 0 ⇒ b² – 4ac = 0
⇒ (2m + 4)² – 4 x (4 – m) (8m + 1) = 0
⇒ 4m² + 16m + 16 – 4 (32m + 4 – 8m² – m) = 0
⇒ 36m² – 108m = 0
⇒ 36m (m – 3) = 0
⇒ m = 0, 3

Que-4: If the roots of ax² + x + b = 0be real and unequal, show that the roots of (x²+1)/x = 4√ab are imaginary.

Sol: Given roots of ax² + x + b = 0 be real and unequal.
∴ discriminant > 0
⇒ 1 – 4ab > 0 …(1)
Also, given quadratic eqn. can be written as,
x² – 4√ab x + 1 = 0 …(2)
On comparing eqn. (2) with Ax² + Bx + C = 0
we have, A = 1 ; B = – 4√ab ; C = 1
Here discriminant = B² – 4AC
= (- 4√ab)² – 4 x 1 x 1
= 16ab – 4 = 4 (4ab – 1)
= – 4(1 – 4ab) < 0 [using eqn. (1)]
Hence the roots of eqn. (2) are imaginary.

Que-5: Find a so that the sum of the roots of the equation ax² + 2x + 3a = 0 may be equal to their product.

Sol: Given quadratic eqn. be
ax² + 2x + 3a = 0 … (1)
On comparing eqn. (1) with
Ax² + Bx + C = 0
we have, A = a; B = 2; C = 3a
∴ Sum of roots = – B/A = – 2/a
product of roots = C/A = 3a/a = 3
It is given that, sum of roots = product of roots
⇒ –2/a = 3 ⇒ a = −2/3

Que-6: If α, ß are the roots of the equation x² + x + 1 = 0, find the value of α³ + ß³.

Sol: Since α, ß are the roots of eqn. x² + x + 1 = 0
∴ S = α + ß = –1/1 = – 1
and P = αß = 1/1 = 1
∴ α³ + ß³ = (α + ß)³ – 3αß (α + ß)
= (- 1)³ – 3 (1)(- 1) = – 1 + 3 = 2

Que-7: If α, ß are the roots of the equation x² + px + q = 0, find the value of
(a) α³ß + αß³
(b) α⁴ + α²ß² + ß⁴.

Sol: Given α and ß are the roots of equation x² + px + q = 0
∴ α + ß = – p ; ap = q
(a) α³ß + αß³ = αß (α² + ß²)
= αß [(α + ß)² – 2αß]
= q (- P)² – 2q] = q(p² – 2q)

(b) b⁴ + α²ß² + ß⁴ = (α² + ß²)² – α²ß²
= [(α + ß)² – 2αß]² – (αß )²
= [(- P)² – 2q]² – q²
= (p² – 2q)² – q²
= p⁴ – 4p²q + 3q²

Que-8: If the roots of the equation x² + px + 7 = 0 are denoted by α and ß, and α² + ß² = 22, find the possible values of p.

Sol: Since it is given that a and p are the roots of equation x² + px + 7 = 0
∴ α + ß = – p ; αß = 7
Also given α² + ß² = 22
⇒ (α + ß)² – 2αß = 22
⇒ (- p)² – 2 x 7 = 22
⇒ p² = 22+ 14 = 36
⇒ p = ± 6

Que-9: If α, ß are the roots of the equation 3x² – 6x + 4 = 0, find the value of
[(α/β)+(β/α)] + 2[(1/α)+(1/β)] + 3αβ

Sol: Given a and p are the roots of equation 3x² – 6x + 4 = 0

1 + 3 + 4 = 8

Que-10: If α, ß are the roots of ax² + bx + c = 0, find the values of
(i) [(α/β)−(β/α)]²
(ii) (α³/β) + (β³/α)

Sol:  Given a and p are the roots of eqn. ax² + bx + c = 0
α+β = -b/a  and   αβ = c/a

Que-11: If the sum of the roots of the equation x² – px + q = 0 be m times their difference, prove that p² (m² – 1) = 4m²p.

Sol: Let α, ß are the roots of equation
x² – px + q = 0 …(1)
∴ α + ß = p ; αß = q
It is given that sum of roots of eqn. (1)
= m x difference of their roots
⇒ α + ß = m|α – ß|
On squaring both sides ; we have
(α + ß)² = m² (α – ß)²
⇒ (α + ß)² = m² [(α + ß)² – 4αß]
⇒ p² = m² [p² – 4q]
⇒ p² (m² – 1) = 4m²q

Que-12: If one root of the equation x² + ax + 8 = 0 is 4 while the equation x² + ax + b = 0 has equal roots, find b.

Sol: Since 4 be the root of equation
x² + ax + 8 = 0 ⇒ 4² + 4a + 8 = 0
⇒ 4a + 24 = 0 ⇒ a = – 6
Since the equation x² + ax + b = 0 has equal roots
∴ Discriminant = 0
⇒ α² – 4b = 0 ⇒ (- 6)² – 4b = 0
⇒ 4b = 36 ⇒ b = 9

Que-13: Find the value of a for which one root of the quadratic equation (a² – 5a + 3) x² + (3a – 1) x + 2 = 0 is twice as large as the other.

Sol: Let α and 2α are the two roots of given equation (a² – 5a + 3)x² + (3a – 1)x + 2 = 0

(3a-1)² = 9 (a²-5a+3)
9a²-6a+1 = 9a²-45a+27
39a = 26
a = 26/39 = 2/3

Que-14: If α, ß are the roots of the equation ax² – bx + b = 0, prove that
√(α/β) + √(β/α) − √(b/a) = 0.

Sol: If α, ß are the roots of the equation ax² – bx + b = 0, prove that
Given α and ß are the roots of the equation ax² – bx + b = 0
∴ α + ß = b/a and αß = b/a
Now, 1/2
= 1/2

Que-15: If α and ß are the roots of the equation x² + x – 7 = 0, form the equation whose roots are α² and ß².

Sol: Given a and P are the roots of the eqn. x² + x – 7 = 0
∴ α + ß = – 1; αß = – 7
Sum of roots of required eqn. = α² + ß² = S
= (α + ß)² – 2αß = (- 1)² – 2 (- 7)
= 15
and product of roots of required equation
= α² p² = (αß)² = (- 7)² = 49
Thus the required quadratic eqn. by given by x² – Sx + P = 0 ⇒ x² – 15x + 49 = 0

Que-16: If α and ß are the roots of the equation 2x² + 3x + 2 = 0, find the equation whose roots are α + 1 and ß + 1.

Sol: Given α and ß are the roots of the eqn.
2x² + 3x + 2 = 0
∴ α + ß = – 3/2 ; αß = 2/2 = 1
∴ S = sum of roots of quadratic eqn.
= α + 1 + ß + 1
= – 3/2 + 2 = 1/2
P = product of roots of quadratic eqn.
= (α + 1)(α + 1)
= αß + (α + ß) + 1
= 1 – 3/2 + 1 = 1/2
Hence the required quadratic eqn. be given by x² – Sx + P = 0 ⇒ x² – 1/2x + 1/2 = 0
⇒ 2x² – x + 1 = 0

Que-17: Find the equation whose roots are α/ß and ß/α, where α and ß are the roots of the equation x² + 2x + 3 = 0.

Sol: Given a and p are the roots of equation x² + 2x + 3 = 0
∴ α + ß = – 2 ; αß = 3
S = sum of roots of required eqn.
= (α/β) + (β/α) = (α²+β²)/αβ
= {(α+β)²−2αβ}/αβ = {(−2)²−2×3}/3 = −2/3
P = product of roots of required eqn.
= α/β ⋅ β/α = 1
Hence the required quadratic eqn. having roots α/ß and ß/α is given by
x² – Sx + P = 0 ⇒ x² – (- 2/3) x + 1 = 0
⇒ 3x² + 2x + 3 = 0

Que-18: If a and p are the roots of the equation 2x² – 3x + 1 = 0, form the equation whose roots are {α/(2β+3)} and {β/(2α+3)}

Sol: Given a and p are the roots of the eqn. 2x² – 3x + 1 = 0

Que-19: If a ≠ b and a² = 5a – 3, b² = 5b – 3, then form that equation whose roots are (a/b) and (b/a)

Sol: Given a ≠ b and a² = 5a – 3 and b² = 5b – 3
∴ a and b are roots of the quadratic equation x² – 5x + 3 = 0
∴ a + b = 5 ; ab = 3
S = sum of roots of required eqn.
= (a/b) + (b/a) = (a²+b²)/ab
= {(a+b)²−2ab}/ab = {5²−2×3}/3 = 19/3
and P = product of roots of required eqn.
= (a/b) × (b/a) = 1
Hence the required quadratic eqn. having roots ab and ba be given by
x² – Sx + P = 0
⇒ x² – x + 1 = 0
⇒ 3x² – 19x + 3 = 0

Que-20: Given that a and P are the roots of the equation x² = x + 7.
(i) Prove that
(a) 1/α = (α−1)/7  and   (b) α³ = 8α + 7.
(ii) Find the numerical value of (α/β) + (β/α).

Sol: (i) Since α be the root of eqn.
x² = x + 7 …(1)
∴ it must satisfies eqn. (1)
∴ α² = α + 7 ⇒ α² – α = 7
⇒ α (α – 1) = 7 ⇒ 1/α = (α−1)/7

(b) Further α³ = α² . α = (α + 7) α
= α² + 7α = α + 7 + 7α
⇒ α³ = 8α + 7

(ii) Since α, ß are the roots of eqn. (1)
∴ α + ß = 1 ; αß = – 7
∴ (α/β) + (β/α) = {α²+β²}/αβ
= {(α+β)²−2αβ}/αβ
= {1²−2×(−7)}/−7 = −15/7

Que-21: Given that α and ß are the roots of the equation x² – x + 7 = 0, find
(i) the numerical value of {α/(β+3)} + {β/(α+3)} ;
(ii) an equation whose roots are {α/(ß+3)} and {ß/(α+3)}.

Sol: Given α and ß are the roots of equation x² – x + 7 = 0
∴ α + ß = + 1 ; αß = 7
(i) S = sum of roots of required eqn.

(ii) Hence the required quadratic eqn. having roots {α/(ß+3)} and {ß/(α+3)}
x² – Sx + P = 0
⇒ x² + (10/19)x + (7/19) = 0
⇒ 19x² + 10x + 7 = 0

Que-22: Given that α and ß are the roots of the equation 2x² – 3x + 4 = 0, find an equation whose roots are α + 1/α and ß + 1/ß.

Sol: Given α and ß are the roots of the eqn.

Thus the required quadratic eqn. having roots α + (1/α) and ß + (1/ß) be given by
x² – Sx + p = 0 ⇒ x² – (9/4)x + (13/8) = 0
⇒ 8x² – 18x + 13 = 0

Que-23: The roots of the quadratic equation x² + px + 8 = 0 are α and ß. Obtain the values of p, if
(i) α = ß²
(ii) α – ß = 2.

Sol: Given α and ß are the roots of the eqn.
x² + px + 8 = 0
∴ α + ß = – p ; αß = 8 … (1)
(i) When α = ß² ∴ from (1); we have
ß³ = 8 ⇒ ß = 2 ∴ α = 2² = 4
∴ from (1) ; – p = 4 + 2 ⇒ p = – 6

(ii) Given α – ß = 2 ;
On squaring both sides ; (α – ß)² = 4
⇒ (α + ß)² – 4αß = 4
⇒ (- p)² – 4 x 8 = 4
⇒ p² = 36 ⇒ p = ± 6

Que-24: If the roots of x² – bx + c = 0 be two consecutive integers, then find the value of b² – 4c.

Sol: Let the roots of eqn.
x² – 6x + c = 0 are α, α + 1
∴ α + α + 1 = b ⇒ 2α + 1 = b …(1)
and α (α + 1) = c …(2)
Eliminating a from eqn. (1) and eqn. (2)
From (1); α = (b–1)/2
∴ from (2); {(b−1)/2} [{(b−1)/2}+1] = c
⇒ {(b−1)/2} {(b+1)/2} = c
⇒ b² – 1 = 4c
⇒ b² – 4c = 1

Que-25: The roots of the equation
px² – 2(p + 2)x + 3p = 0 are α and ß. If α – ß = 2, calculate the value of α, ß and p.

Sol: Given a and p are the roots of the equation
px² – 2(p + 2)x + 3p = 0 = 0
∴ α + ß = {2(p+2)}/p ; αß = 3p/p = 3
Also given α – ß = 2 ; on squaring both sides; we have

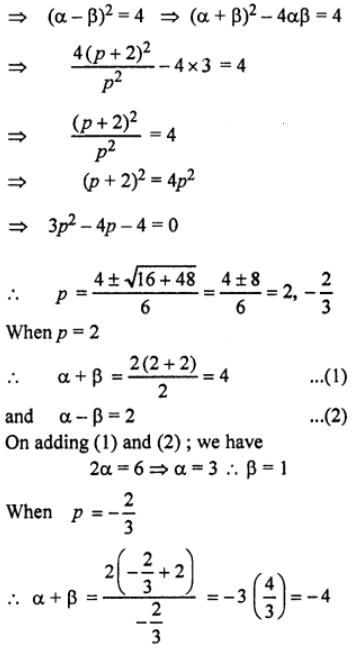
On solving eqn. (2) and (3); we have α = – 1 and ß = – 3

Que-26: The roots of the equation ax² + bx + c = 0 are α and ß. Form the quadratic equation whose roots are α + (1/ß) and ß + (1/α)

Sol: Given α and ß are the roots of the eqn. ax² + bx + c = 0

Thus the required quadratic eqn. having roots α + (1/ß) and ß + (1/α) is given by
x² – Sx + P = 0
⇒ x² + [{b(c+a)x}/ac] + {(a+c)²/ac} = 0
⇒ acx² + b (c + a) x + (a + c)² = 0

Que-27: Two candidates attempt to solve a quadratic equation of the form x² + px + q = 0. One starts with a wrong value of p and finds the roots to be 2 and 6. The other starts with a wrong value of q and finds the roots to be 2 and – 9. Find the correct roots and the equation.

Sol: One candidate find the roots of given eqn.
x² + px + q = 0 …(1)
are 2 and 6 ∴ it forms the quadratic eqn. as
(x – 2) (x – 6) = 0
⇒ x² – 8x + 12 = 0 …(2)
∴ Correct value of q = 12 [on comparing eqn. (1) and eqn. (2)]
[since value of p is given to be wrong]
Other candidate find the roots of eqn. (1) are 2 and – 9 ∴ he forms the quadratic eqn. as : (x – 2) (x + 9) = 0
⇒ x² + 7x – 18 = 0 …(3)
So on comparing eqn. (1) and eqn. (3) ;
we have Correct value of p = 7
Hence the correct values of p and q are 7 and 12
∴ required eqn. becomes; x² + 7x + 12 = 0
⇒ (x + 3) (x + 4) = 0 ⇒ x = – 3, – 4
Hence the correct roots of given eqn. are – 3 and – 4.

Que-28: Given that a and P are the roots of the equation x² = 7x + 4.
(i) Show that α³ = 53α + 28
(ii) find the value of (α/β) + (β/α).

Sol: Since α and ß are the roots of eqn. x² = 7x + 4
i. e. x² – 7x – 4 = 0 …(1)
∴ α + ß = 7 and αß = – 4
Since a be the root of eqn. (1) ∴ it satisfies eqn. (1)
∴ α² = 7α + 4
⇒ α³ = 7α² + 4α = 7 (7α + 4) + 4α = 53α + 28

(ii) (α/β) + (β/α) = (α²+β²)/αβ
= {(α+β)²−2αβ}/αβ
= {7²−2×(−4)}/−4
= 57/−4

Que-29: The ratio of the roots of the equation x² + αx + α + 2 = 0 is 2. Find the values of the parameter a.

Sol: Since the ratio of the roots of the equation x² + αx + α + 2 = 0 is 2.
Let 2ß and ß are the roots of given equation.
∴ 2ß + ß = – a ⇒ 3ß = – α …(1)
and (2ß) ß = α + 2 ⇒ 2ß² = α + 2 …(2)
From (1) and (2); we have
2 (−α/3)² = α+2
⇒ 2×(α²/9) = α+2
⇒ 2α² – 9α – 18 = 0
∴ α = [9±√{81+4×2×18}]/(2×2)
= (9±15)/4
∴ α = 6, – 3/2

Que-30: If (1 – p) is a root of the quadratic equation x² + px + (1 – p) = 0, then its roots are
(a) 0, – 1
(b) – 1, 1
(c) 0, 1
(d) – 1, 2

Sol: Since (1 – p) be the root of quadratic equation
x² + px + (1 – p) = 0 …(1)
⇒ (1 – p)² + p(1 – p) + (1 – p) = 0
⇒ (1 – P) [1 – p + p + 1] = 0
⇒ 2(1 – p) = 0
⇒ p = 1
∴ eqn. (1) becomes ; x² + x = 0
⇒ x (x + 1) = 0 ⇒ x = 0, – 1
Hence the required roots of given equation are 0 and – 1.

–: End of Quadratic Equations Class 11 OP Malhotra Exe-10C ISC Maths Ch-10 Solutions. :–

Return to :- OP Malhotra ISC Class-11 S Chand Publication Maths Solutions

Thanks

Please share with your friends