ML Aggarwal Quadratic Equations Exe-5.1 Class 10 ICSE Maths Solutions . We Provide Step by Step Answer of Exe-5.1 Questions for Quadratic Equations in One Variable as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-10.
ML Aggarwal Ch-5 Quadratic Equations in one Variable Exercise- 5.1 Class 10 ICSE Maths Solutions
| Board | ICSE |
| Subject | Maths |
| Class | 9th |
| Chapter-5 | Quadratic Equations |
| Writer / Book | Understanding |
| Topics | Solutions of Exe-5 |
| Academic Session | 2024-2025 |
Quadratic Equations in one Variable Exe-5.1
(Class 10 ICSE ML Aggarwal Maths Solutions)
Question -1. In each of the following, determine whether the given numbers are roots of the given equations or not.
(i) x² – 5x + 6 = 0; 2, – 3
(ii) 3x² – 13x – 10 = 0; 5,(-2/3)
Answer:
(i) x² – 5x + 6 = 0; 2, – 3

(ii) 3x² – 13x – 10 = 0; 5,(-2/3)
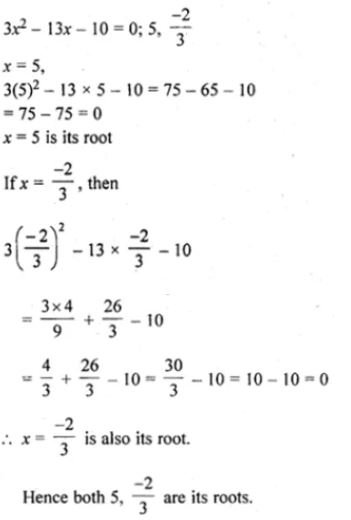
Question- 2. In each of the following, determine whether the given numbers are solutions of the given equation or not:
(i) x² – 3√3x + 6 = 0; √3, – 2√3
(ii) x² – √2x – 4 = 0, x = – √2, 2√2
Answer :
(i) x² – 3√3x + 6 = 0; √3, -2√3
Substituting the value of x = √3
x2 – 3√3x + 6 = 0
(√3)2 – 3√3(√3) + 6 = 0
3 – 9 + 6 = 0
-9 + 9 =0
0 = 0
∴ √3 is the solution of the equation.
When, x = -2√3
x2 – 3√3x + 6 = 0
(-2√3)2 – 3√3(-2√3) + 6 = 0
4(3) +18 + 6 = 0
12 + 18 + 6 = 0
36 =0
∴ -2√3 is not the solution of the equation.
(ii) x2 – √2x – 4 = 0; x = -√2, 2√2
Let us substitute the given values in the expression and check,
When, x = -√2
x2 – √2x – 4 = 0
(-√2)2 – √2(-√2) – 4 = 0
2 + 2 – 4 = 0
4 – 4 = 0
0 = 0
∴ -√2 is the solution of the equation.
When, x = 2√2
x2 – √2x – 4 = 0
(2√2)2 – √2(2√2) – 4 = 0
4(2) – 4 – 4 = 0
4 – 4 = 0
0 = 0
∴ 2√2 is the solution of the equation
Question- 3.
(i) If (-1/2) is a solution of the equation 3x² + 2kx – 3 = 0, find the value of k.
(ii) If 2/3 is a solution of the equation 7x² + kx – 3 = 0, find the value of k.
Answer:
(i) If –1/2 is a solution of the equation 3x² + 2kx – 3 = 0, find the value of k.
Let us substitute the given value x = -1/2 in the expression, we get
3x² + 2kx – 3 = 0
3(-1/2)2 + 2k(-1/2) – 3 = 0
3/4 – k – 3 = 0
¾ – 3 = k
By taking LCM
k = (3-12)/4
= -9/4
∴ Value of k = -9/4.
(ii) If 2/3 is a solution of the equation 7x² + kx – 3 = 0, find the value of k.
Let us substitute the given value x = 2/3 in the expression, we get
7x² + kx – 3 = 0
7(2/3)2 + k(2/3) – 3 = 0
7(4/9) + 2k/3 – 3 = 0
28/9 – 3 + 2k/3 = 0
2k/3 = 3 – 28/9
By taking LCM on the RHS
2k/3 = (27 – 28)/9
= -1/9
k = -1/9 × (3/2)
= -1/6
∴ Value of k = -1/6.
Question -4.
(i) If √2 is a root of the equation kx² + √2 – 4 = 0, find the value of k.
(ii) If a is a root of the equation x² – (a + b)x + k = 0, find the value of k.
Answer:
(i) kx² + √2 – 4 = 0, x = √2
x = √2 is its solution
(i) If √2 is a root of the equation kx² + √2x – 4 = 0, find the value of k.
Let us substitute the given value x = √2 in the expression, we get
kx² + √2x – 4 = 0
k(√2)2 + √2(√2) – 4 = 0
2k + 2 – 4 = 0
2k – 2 = 0
k = 2/2
= 1
∴ Value of k = 1.
(ii) If a is a root of the equation x² – (a + b)x + k = 0, find the value of k.
Let us substitute the given value x = a in the expression, we get
x² – (a + b)x + k = 0
a2 – (a + b)a + k = 0
a2 – a2 – ab + k = 0
-ab + k = 0
k = ab
∴ Value of k = ab.
Question -5. If 2/3 and – 3 are the roots of the equation px² + 7x + q = 0, find the values of p and q.
Answer -5
2/3 and – 3 are the roots of the equation px² + 7x + q = 0
Substituting the value of x = and – 3 respectively, we get
px² + 7x + q = 0
p(2/3)2 + 7(2/3) + q = 0
4p/9 + 14/3 + q = 0
By taking LCM
4p + 42 + 9q = 0
4p + 9q = – 42 … (1)
Now, substitute the value x = -3 in the expression, we get
px² + 7x + q = 0
p(-3)2 + 7(-3) + q = 0
9p + q – 21 = 0
9p + q = 21
q = 21 – 9p…. (2)
By substituting the value of q in equation (1), we get
4p + 9q = – 42
4p + 9(21 – 9p) = -42
4p + 189 – 81p = -42
189 – 77p = -42
189 + 42 = 77p
231 = 77p
p = 231/77
p = 3
Now, substitute the value of p in equation (2), we get
q = 21 – 9p
= 21 – 9(3)
= 21 – 27
= -6
— : End of ML Aggarwal Quadratic Equations Exe-5.1 Class 10 ICSE Maths Solutions :–
Return to :- ML Aggarwal Solutions for ICSE Class-10
Thanks
Please Share with Your Friends



Thank you so much
It helped me a lot
thanks
Thank you so much