Quadrilateral ICSE Class-6th Concise Selina Mathematics Solutions Chapter-27. We provide step by step Solutions of Exercise / lesson-27 Quadrilateral for ICSE Class-6 Concise Selina Mathematics.Our Solutions contain all type Questions of Exe-27 A and Exe-27 B with Notes on Quadrilateral to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-6.
Quadrilateral ICSE Class-6th Concise Selina Mathematics Solutions Chapter-27
–: Select Topics :–
A quadrilateral is a plane figure that has four sides or edges, so having four corners or vertices. Quadrilaterals will typically be of standard shapes with four sides like rectangle, square, trapezoid, and kite or irregular and uncharacterized
Types of Quadrilaterals
There are many types of quadrilaterals. As the word ‘Quad’ means four, all these types of a quadrilateral have four sides and the sum of angles of these shapes is 360 degrees.
- Trapezium
- Parallelogram
- Squares
- Rectangle
- Rhombus
- Kite
Another way to classify the types of quadrilaterals are:
- Convex Quadrilaterals: Both the diagonals of a quadrilateral are completely contained within a figure.
- Concave Quadrilaterals: At least one of the diagonals lies partly are entirely outside of the figure.
- Intersecting Quadrilaterals: Intersecting quadrilaterals are not simple quadrilaterals in which the pair of non-adjacent sides intersect. This kind of quadrilaterals are known as self-intersecting or crossed quadrilaterals
Quadrilateral Properties
A quadrilateral is a 4-sided plane figure. Below are some important properties of quadrilaterals :
- Every quadrilateral has 4 vertices, 4 angles, and 4 sides
- The total of its interior angles = 360 degrees
- A quadrilateral with four equal sides and four right angles is a square
- A quadrilateral that has opposite sides equal and measure of every angle is 90 degrees is a rectangle
- Parallelogram, trapezium, rhombus, and kite are other examples of quadrilaterals
Notes on Quadrilateral
A quadrilateral is a trapezoid or a trapezium if 2 of its sides parallel to each other.
A quadrilateral is a parallelogram if 2 pairs of sides parallel to each other.
Squares and Rectangles are special types of parallelograms. Below are some special properties.– All internal angles are of “right angle” (90 degrees).– Each figure contains 4 right angles.– Sides of a square are of the same length (all sides are congruent) – Opposite sides of a rectangle are same.– Opposite sides of a rectangle and square are parallel.
A quadrilateral is a rhombus, if All the sides are of equal length-Specified 2 pairs of sides are parallel to each other.
A kite is a special sort of quadrilateral, wherever 2 pairs of adjacent sides are equal to each other.
Exercise – 27 A Quadrilateral ICSE Class-6th Concise Mathematics Selina Solutions
Question -1.
Two angles of a quadrilateral are 89° and 113°. If the other two angles are equal; find the equal angles.
Answer-1
Let the other angle = x°
According to given,
89° + 113° + x° + x° = 360°
2x° = 360° – 202°
2x° = 158°
x° = 158⁄2 =79°
∴other two angles = 79° each
Question- 2.
Two angles of a quadrilateral are 68° and 76°. If the other two angles are in the ratio 5 : 7; find the measure of each of them.
Answer-2
Two angles are 68° and 76°
Let other two angles be 5x and 7x
∴ 68°+76°+5x + 7x = 360°
12x + 144° = 360°
12x = 360° – 144°
12x= 216°
x = 18°
angles are 5x and 7x
i.e. 5×18° and 7×18° i.e. 90° and 126°
Question -3.
(i) the value of x.
(ii) each angle of the quadrilateral.
Answer-3
(i) the value of x.
Angles of quadrilateral are,
(4x)°, 5(x+2)°, (7x-20)° and 6(x+3)°.
4x+5(x+2)+(7x-20)+6(x+3) = 360°
4x+5x+10+7x-20+6x+18 = 360° 22x+8 = 360°
22x = 360°-8°
22x = 352°
x = 16°
(ii) each angle of the quadrilateral.
Hence angles are,
(4x)° = (4×16)° = 64°,
5(x+2)° = 5(16+2)° = 90°,
(7x-20)° = (7×16-20)° = 92°
6(x+3)° = 6(16+3) = 114°
Question- 4.
(i) x
(ii) ∠B and ∠C

Answer-4
(i) x
∵ ∠A = 90° (Given)
∠B = (2x+4°)
∠C = (3x-5°)
∠D = (8x – 15°)
∠A + ∠B + ∠C + ∠D = 360°
90° + (2x + 4°) + (3x – 5°) + (8x – 15°) = 360°
90° + 2x + 4° + 3x – 5° + 8x – 15° = 360°
⇒ 74° + 13x = 360°
⇒13x = 360° – 74°
⇒ 13x = 286°
⇒ x = 22°
(ii) ∠B and ∠C
∵ ∠B = 2x + 4 = 2. x 22° + 4 – 48°
∠C = 3x – 5 = 3×22° -5 = 61°
Hence (i) 22° (ii) ∠B = 48°, ∠C = 61°
Question -5.
(i) Calculate each angle of the quadrilateral.
(ii) Assign a special name to quadrilateral ABCD.
Answer-5
(i) Calculate each angle of the quadrilateral.
∵∠A : ∠D = 1:2
Let ∠A = x and ∠B = 2x
∵∠C : ∠B = 4 : 5 Let ∠C = 4y and ∠B = 5y
∵AB || DC
∠A + ∠D = 180° x + 2x = 180°
3x = 180° x = 60°
∴A = 60°
∠D = 2x = 2 x 60 = 120° Again ∠B + ∠C = 180°
5y + 4y= 180°
9y = 180°
y = 20°
∴∠B = 5y- = 5 x 20 = 100°
∠C = 4y = 4 x 20 = 80°
Hence ∠A = 60° ; ∠B = 100° ; ∠C = 80° and ∠D = 120°
(ii) Assign a special name to quadrilateral ABCD.
Trapezium
Question- 6.
(i) x,
(ii) ∠ABC,
(iii) ∠ACD.
Answer-6
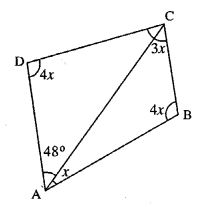
(i) In Quadrilateral ABCD,
x + 4x + 3x + 4x + 48° = 360°
12x = 360° – 48°
12x =312
(ii) ∠ABC = 4x
4 x 26 = 104°
(iii) ∠ACD = 180°-4x-48°
= 180°-4×26°-48°
= 180°-104°-48°
= 180°-152° = 28°
Question- 7.
Given : In quadrilateral ABCD ; ∠C = 64°, ∠D = ∠C – 8° ;
∠A = 5(a+2)° and ∠B = 2(2a+7)°.
Calculate ∠A.
Answer-7
∵∠C = 64° (Given)
∴∠D = ∠C- 8°
= 64°- 8°
= 56°
∠A = 5 (a + 2)°
∠B = 2(2a + 7)°
Now ∠A + ∠B + ∠C + ∠D = 360°
5(a + 2)° + 2(2a + 7)° + 64°+ 56° = 360°
5a + 10 + 4a + 14° + 64° + 56° = 360°
9a + 144° = 360°
9a = 360°-144°
9a = 216°
a = 24°
∴∠A = 5(a + 2)
= 5(24 + 2)
= 130°
Question -8.
In the given figure :
∠b = 2a + 15
and ∠c = 3a+5; find the values of b and c.

Answer-8
∠b = 2a + 15
& ∠c = 3a + 5
∵Sum of angles of quadrilateral = 360°
70° + a + 2a + 15 + 3a + 5 – 360°
6a+90° = 360°
6a = 270°
a = 45°
∴ b = 2a+15= 2×45+15 = 105°
c = 3a+5 = 3×45+5 = 140°
105° and 140
Question- 9.
Three angles of a quadrilateral are equal. If the fourth angle is 69°; find the measure of equal angles.
Answer-9
Let each equal angle be
x° x + x + x + 69° = 360°
3x = 360°-69 3x =291 x = 97°
Each equal angle = 97°
Question -10.
In quadrilateral PQRS, ∠P : ∠Q : ∠R : ∠S = 3 : 4 : 6 : 7.
Calculate each angle of the quadrilateral and then prove that PQ and SR are parallel to each other. Is PS also parallel to QR ?
Answer-10
∵∠P : ∠Q : ∠R : ∠S = 3 : 4 : 6 : 7
Let ∠P = 3x
∠Q = 4x
∠R = 6x & ∠S = 7x
∴∠P+∠Q+∠R+∠S = 360°
3x + 4x + 6x + lx = 360°
20x = 360°
x = 18°
∴ ∠P = 3x = 3×18 = 54°
∠Q = 4x = 4×18 = 72°
∠R = 6x = 6×18 = 108°
∠S = 7x = 7×18 = 126°
∠Q + ∠R = 72°+108° = 180° or ∠P +∠S = 54°+126° = 180°
Hence PQ || RS
As ∠P + ∠Q = 72° +54° = 126°
Which is * 180°.
∴PS and QR are not parallel.
Question -11.
Use the information given in the following figure to find the value of x.
Answer-11
Take A, B, C, D as the vertices of quadrilateral and BA is produced to E

Since ∠EAD = 70°
∴∠DAB = 180° – 70° = 110° [∵ EAB is a straight line and AD stands on it]
∴∠EAD + ∠DAB = 180°
∴110° + 80° + 56° + 3x = 360°
[∵ sum of interior angles of a quadrilateral = 360°]
∴3x = 360° – 110° – 80° – 56° + 6°
3x = 360° – 240° = 120°
∴x = 40°
Question -12.
The following figure shows a quadrilateral in which sides AB and DC are parallel.
If ∠A : ∠D = 4 : 5, ∠B = (3x – 15)° and ∠C = (4x + 20)°, find each angle of the quadrilateral ABCD.

Answer-12
Let ∠A = 4x
∠D = 5x
Since ∠A + ∠D = 180° [∵ AB || DC]
∴4x + 5x = 180°
⇒ 9x = 180° ⇒x = 20°
∴∠A = 4 (20) = 80°, ∠D = 5 (20) = 100° Again ∠B + ∠C = 180° [ ∵ AB || DC]
∴ 3x – 15° + 4x + 20° = 180°
7x = 180°-5°
⇒ 7x = 175° ⇒ x = 25°
∴∠B = 75°-15° = 60° and ∠C = 4(25) + 20 = 100° + 20° = 120°
Selina Solutions of Quadrilateral Exe-27 B for ICSE Class-6th Concise Mathematics
Question -1.
In a trapezium ABCD, side AB is parallel to side DC. If ∠A = 78° and ∠C = 120°, find angles B and D.
Answer-1
∵ AB || DC and BC is transversal
∴∠B and ∠C, ∠A and ∠D are Co-interior angles with their sum = 180°
i.e. ∠B + ∠C = 180°
⇒ ∠B + 120° = 180°
⇒ ∠B = 180° – 120°
⇒ ∠B = 60°
Also ∠A + ∠D = 180°
⇒ 78° + ∠D = 180°
⇒ ∠D = 180° – 78°
∠D = 102°
Question -2.
In a trapezium ABCD, side AB is parallel to side DC. If ∠A = x° and ∠D = (3x – 20)°; find the value of x.
Answer-2
∵AB || DC and BC is transversal
∴∠A and ∠B are Co-interior angles with their sum = 180°
i.e. ∠A + ∠D = 180°

⇒ x° + (3x – 20)° = 180°
⇒ x° + 3x° – 20° = 180°
⇒ 4x° = 180° + 20°
x° = 200⁄4 = 50°
∴Value of x = 50°
Question -3.
The angles A, B, C and D of a trapezium ABCD are in the ratio 3 : 4 : 5 : 6.
Le. ∠A : ∠B : ∠C : ∠D = 3:4: 5 : 6. Find all the angles of the trapezium. Also, name the two sides of this trapezium which are parallel to each other. Give reason for your answer
Answer-3
As the trapezium ABCD is a quadrilateral,
∴ Sum of its interior angles = 360°
⇒ ∠A + ∠B + ∠C + ∠D = 360°
⇒ 3x + 4x + 5x + 6x = 360°
⇒ 18x = 360°
⇒ x = 360⁄18 =20°
∴ ∠A = 3x = 3 × 20° = 60°
and ∠B = 4x = 4 × 20° = 80°
and ∠C = 5x = 5 × 20° = 100°
and ∠D = 6x = 6 × 20° = 120°
AB is parallel to DC.
∵ ∠A + ∠D = 180°
∠A and ∠D are co-interior angles whose sum = 180°
Question -4.
In an isosceles trapezium one pair of opposite sides are ….. to each Other and the other pair of opposite sides are ….. to each other.
Answer-4
In an isosceles trapezium one pair of opposite sides are parallel to each other and the other pair of opposite sides are equal to each other.
Question -5.
Two diagonals of an isosceles trapezium are x cm and (3x – 8) cm. Find the value of x.
Answer-5
∵The diagonals of an isosceles trapezium are of equal length
∴3x – 8 = x
⇒ 3x – x = 8 cm
⇒ 2x = 8 cm
⇒ x = 4 cm
∴ The value of x is 4 cm
Question- 6.
Angle A of an isosceles trapezium is 115° ; find the angles B, C and D.
Answer-6
Since, the base angles of an isosceles trapezium are equal,
∴ ∠A = ∠B = 115°
Also, ∠A and ∠D are co-interior angles and their sum = 180°
∴ ∠A + ∠D = 180°
⇒115° + ∠D = 180°
⇒ ∠D = 180° – 115°
⇒ ∠D = 650°
Also, ∠D = ∠C = 65°
∴ ∠B = 115°, ∠C = 65°, ∠D = 65°
Question -7.
Two opposite angles of a parallelogram are 100° each. Find each of the other two opposite angles.
Answer-7
Given : Two opposite angles of a parallelogram are 100° each
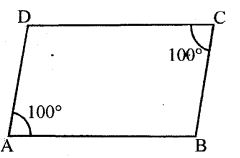
∵ Adjacent angles of a parallelogram are supplementary,
∴∠A + ∠B = 180°
⇒ 100° + ∠B = 180°
⇒ ∠B = 180° – 100°
⇒ ∠B = 80°
Also, opposite angles of a parallelogram are equal
∴∠D = ∠B = 80°
∴∠B = ∠D = 80°
Question- 8.
Two adjacent angles of a parallelogram are 70° and 110° respectively. Find the other two angles of it.
Answer-8
Given two adjacent angles of a parallelogram are 70° and 110° respectively.

Since, we know that opposite angles of a parallelogram are equal
∴∠C = ∠A = 70° and ∠D = ∠B = 110°
Question -9.
The angles A, B, C and D of a quadrilateral are in the ratio 2:3: 2 : 3. Show this quadrilateral is a parallelogram.
Answer-9
Given, Angles of a quadrilateral are in the ratio 2: 3: 2: 3
i.e. A : B : C : D are in the ratio
2: 3: 2: 3
To prove: Quadrilateral ABCD is a parallelogram
Proof: Let us take ∠A = 2x, ∠B = 3x, ∠C = 2x and ∠D = 3x
We know, that the sum of interior angles of a quadrilateral = 360°
⇒ ∠A + ∠B + ∠C + ∠D = 360°
⇒ 2x + 3x + 2x + 3x = 360°
⇒ 10x = 360°
⇒ x = 360⁄10 =36∘
∴ ∠A = ∠C = 2x = 2 × 360° = 72°
∠B = ∠D = 3x = 3 × 36° = 360°
Now, A quadrilateral ABCD is considered as a parallelogram.
(i) When opposite angles are equal,
i.e. ∠A = ∠C = 72° and ∠B = ∠D = 108°
(ii) When adjacent angles are supplementary
i.e. ∠A + ∠B = 180°
and ∠C = ∠D = 180°
⇒ 72° + 108° and 72° + 108° = 180°
⇒ 180° = 180° and 180° = 180°
Since quadrilateral ABCD fulfills the conditions.
∴ Quadrilateral ABCD is a parallelogram.
Question- 10.
In a parallelogram ABCD, its diagonals AC and BD intersect each other at point O.

If AC = 12 cm and BD = 9 cm ; find; lengths of OA and OD.
Answer-10
∵ When diagonals AC and BD intersect each other at point O,
then OA = OC = 1⁄2 AC
and OB = OD = 1⁄2 BD
∴ OA = 1⁄2×AC= 1⁄2×12 =6 cm
and OB = 1⁄2×BD= 1⁄2×9=4.5 cm
Question -11.
In parallelogram ABCD, its diagonals intersect at point O. If OA = 6 cm and OB = 7.5 cm, find the length of AC and BD.

Answer-11
∵ When diagonals AC and BD intersect each other at point O,
then OA = OC = 1⁄2 AC
and OB = OD = 1⁄2 BD
∴ OA = 1⁄2× AC ⇒ AC = 2 × OA
⇒ AC = 2 × 6 cm = 12 cm,
and OB = 1⁄2×BD ⇒ BD = 2 × OB
⇒ BD = 2 × 7.5 cm ⇒ BD = 15 cm
Question- 12.
In parallelogram ABCD, ∠A = 90°
(i) What is the measure of angle B.
(ii) Write the special name of the parallelogram.
Answer-12
In parallelogram ABCD, ∠A = 90°
(i) ∵ In a parallelogram, adjacent angles are supplementary
∴ ∠A + ∠B = 180°
⇒ 90° + ∠B = 180°
⇒ ∠B = 180° – 90°
⇒ ∠B = 90°
(ii) The name of the given parallelogram is a rectangle.
Question- 13.
One diagonal of a rectangle is 18 cm. What is the length of its other diagnol?
Answer-13
∵ In a rectangle, diagonals are equal
⇒ AC = BD
Given, one diagonal of a rectangle = 18cm
∴ Other diagonal of a rectangle will be = 18cm
i.e. AC = BD = 18cm.
Question- 14.
Each angle of a quadrilateral is x + 5°. Find :
(i) the value of x
(ii) each angle of the quadrilateral.
Give the special name of the quadrilateral taken.

Answer-14
(i) We have,
∠A + ∠B + ∠C + ∠D = 360°
∵ We know that the sum of interior angles of a quadrilateral is 360°
∴ ∠A + ∠B + ∠C + ∠D = 360°
⇒ x + 5° + x + 5° + x + 5° + x + 5° = 360°
⇒ 4x + 20° = 360°
⇒ 4x = 360° – 20°
⇒ x=340⁄4 =85°
(ii) Each angle of the quadrilateral ABCD = x + 5°
= 85° + 5°
= 90°
The name of the given quadrilateral is a rectangle.
Question- 15.
If three angles of a quadrilateral are 90° each, show that the given quadrilateral is a rectangle.
Answer-15
The given quadrilateral ABCD will be a rectangle, if its each angle is 90°
Since, the sum of interior angles of a quadrilateral is 360°.
∴∠A +∠B + ∠C + ∠D = 360°
⇒ 90° + 90° + 90° + ∠D = 360°
⇒ 270° + ∠D = 360°
⇒ ∠D = 360° – 270°
⇒ ∠D = 90°
Since, each angle of the quadrilateral is 90°. ∴The given quadrilateral is a rectangle.
Question -16.
The diagonals of a rhombus are 6 .cm and 8 cm. State the angle at which these diagonals intersect.
Answer-16
The diagonals of a Rhombus always intersect at 90°.
Question -17.
Write, giving reason, the name of the figure drawn alongside. Under what condition will this figure be a square.

Answer-17
Since, all the sides of the given figure are equal.
i.e. AB = BC = CD = DA = 6 cm
∴ The given figure is a rhombus.
This figure shall be considered as a square, if any angle is 90°.
Question- 18.
Write two conditions that will make the adjoining figure a square.

Answer-18
The conditions that will make the ad-joining figure a square are :
(i) All sides must be equal.
(ii) Any angle is 90°.
–: End of Quadrilateral ICSE Class-6th Concise Solutions :–
Return to – Concise Selina Maths Solutions for ICSE Class -6
Thanks


