ML Aggarwal Ratio and Proportion Exe-8.1 Class 6 ICSE Maths Solutions

ML Aggarwal Ratio and Proportion Exe-8.1 Class 6 ICSE Maths Solutions. We Provide Step by Step Answer of  Exe-8.1 Questions for Ratio and Proportion as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-6.

ML Aggarwal Ratio and Proportion Exe-8.1 Class 6 ICSE Maths Solutions

Board	ICSE
Publications	Avichal Publishig Company (APC)
Subject	Maths
Class	6th
Chapter-8	Ratio and Proportion
Writer	ML Aggarwal
Book Name	Understanding
Topics	Solution of Exe-8.1 Questions
Edition	2023-2024

Ratio and Proportion Exe-8.1

ML Aggarwal Class 6 ICSE Maths Solutions

Page-160

Question 1. Express the following ratios in simplest form:

(i) 20 : 40
(ii)40 : 20
(iii) 81 : 108
(iv) 98 : 63

Answer:

(i) 20 : 40 = 20/40 = ½ = 1 : 2

(ii) 40 : 20 = 40/20 = 2/1 = 2 : 1

(iii) 81 : 108 = 81/108 = 9/12 = ¾ = 3 : 4

(iv) 98 : 63 = 98/63 = 14/9 = 14 : 9

Question 2. Fill in the missing numbers in the following equivalent ratios:

Answer:

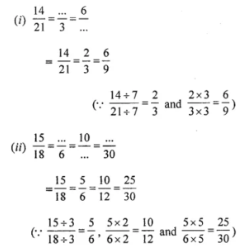
Question 3. Find the ratio of each of the following in simplest form :

(i) 2.1 m to 1.2 m
(ii) 91 cm to 1.04m
(iii) 3.5 kg to 250gm
(iv) 60 paise to 4 rupees
(v) 1 minute to 15 seconds
(vi) 15 mm to 2 cm

Answer:

(i) 2.1 m : 1.2 m

= 2.1/ 1.2

= 21/12 × 10/10

= 7 : 4

(ii) 91 cm : 1.04mm or (1.04 × 100) cm = 104 cm [As 1 m = 100 cm]

= 91 cm : 104 cm

= 91/104

= 7 : 8

(iii) 3.5 kg : 250 gm or (3.5 × 1000) gm : 250 gm [As 1 kg = 1000 gm]

= 3500 gm : 250 gm

= 3500/250

= 14/1

= 14 : 1

(iv) 60 paise : 4 rupees or 60 paise : (4 × 100) paise [As 1 Rs = 100 paise]

= 60 paise : 400 paise

= 60/400

= 6/40

= 3/20

= 3 : 20

(v) 1 minute : 15 seconds or 60 seconds : 15 seconds [As 1 minute = 60 seconds]

= 60 : 15

= 60/15

= 4/1

= 4 : 1

(vi) 15 mm : 2 cm or 15 mm : (2 × 10) mm [As 1 cm = 10 mm]

= 15 mm : 20 mm

= 15/20

= 3/4

= 3 : 4

Question 4. The length and the breadth of a rectangular park are 125 m and 60 m respectively. What is the ratio of the length to the breadth of the park?

Answer:

Length of rectangular park = 125 m
Breadth of rectangular park = 60 m
∴ Ratio of the length to the breadth of park is

125/60 = 25/12 = 25 : 12

Question 5. The population of village is 4800. If the numbers of females is 2160, find the ratio of males to that of females.

Answer:

Population of village = 4800
No. of females = 2160
No. of males = 4800 – 2160 = 2640
No. of males : No. of females
2640 : 2160

= 2640/2160

= 264/216

= 11/9

= 11 : 9

Question 6. In a class, there are 30 boys and 25 girls. Find the ratio of the numbers of

(i) boys to that of girls.
(ii) girls to that of total number of students.
(iii) boys to that of total numbers of students.

Answer:

Boys = 30, girls = 25

Total students = 30 + 25 = 55

(i) boys : girls = 30 : 25

= 30/25 = 6/5 = 6 : 5

(ii) girls : Total no. of students = 25 : 55

= 25/55 = 5/11 = 5 : 11

(iii) Boys : Total no. of students = 30 : 55

= 30/55 = 6/11 = 6 : 11

Question 7. In a year, Reena earns ₹ 1,50,000 and saves ₹ 50,000. Find the ratio of

(i) money she earns to the money she saves.
(ii) money that she saves to the money she spends.

Answer:

(i) Ratio of money that Reena earns to the money she saves

= 150000/50000

= (150000 ÷ 50000)/(50000 ÷ 50000)

= 3/1 = 3 : 1

(ii) Money that she spends
= ₹ 1,50,000 – ₹50,000 = ₹1,00,000
∴ Ratio of money she saves to the money she spends

= 50000/100000

= (50000 ÷ 50000)/(100000 ÷ 50000)

= 1/2 = 1 : 2

Question 8. The monthly expenses of a student have increased from ₹350 to ₹500. Find the ratio of

(i) increase in expenses and original expenses.
(ii) original expenses to increased expenses.
(iii) increased expenses to increased in expenses.

Answer:

Original exp. = ₹350
Increased exp. = ₹500
Increased in exp. = 500 – 350 = ₹150
(i) Increased in exp : original exp.

= 150 : 350

= 150/350 = 15/35 = 3/7 = 3 : 7

(ii) Original exp. : Increased exp.

350 : 500

= 350/500 = 35/50 v= 7/10 = 7 : 10

(iii) Increased exp : Increase in exp.

500 : 150

= 500/150 = 50/15 = 10/3 = 10 : 3

---

Ratio and Proportion Exe-8.1

ML Aggarwal Class 6 ICSE Maths Solutions

Page-161

Question 9. Mr Mahajan and his wife are both school teachers and earn ₹20900 and ₹ 18700 per month respectively. Find the ratio of

(i) Mr Mahajan’s income to his wife’s income.
(ii) Mrs Mahajan’s income to the total income of both.

Answer:

(i) Ratio in Mr Mahajan’s income and his wife
= 20900 : 18700

= 20900/18700

= 19/17

= 19 : 17

(ii) Mrs Mahajan’s income to the total income of both
Earning of Mrs Mahajan = ₹20900
and his wife = ₹ 18700
Total income = ₹39,600
Mrs Mahajan’s income to the total income of both

18700/39600

= 17/36

= 17 : 36

Question 10. Out of 30 students in a class, 6 like football, 12 like cricket and remaining like tennis. Find the ratio of

(a) Number of students liking football to number of students liking tennis.
(b) Number of students liking cricket to total number of students.

Answer:

Students who like football in the class =6
Students who like cricket in the class =12
The remaining students who like tennis can be obtained by subtracting students who like football and cricket from the total students.

= 30−6−12
= 30−18
= 12

(a) The ratio of the number of students liking football to the number of students liking tennis = 6/12 = 1/2

The ratio of the number of students liking football to the number of students liking tennis is 1:2.

(b) The ratio of the number of students liking cricket to the total number of students = 12/30 = 2/5
The ratio of the number of students liking cricket to the total number of students is 2:5

Question 11. Which ratio is greater ?

(i) 3 : 4 or 2 : 3

(ii) 11 : 21 or 15 : 28

Answer:

Question 12. Divide ₹ 560 between Ramu and Munni in the ratio 3 : 2.

Answer:

Total amount = ₹ 560
Ratio in Ramu and Munni = 3 : 2
Sum of ratios = 3 + 2 = 5
Ramu shares = ₹ (560 x 3)/5 = ₹336
Munni shares = ₹ (560 x 2)/5 = ₹224

Question 13. Two people invested ₹ 15000 and ₹25000 respectively to start a business. They decided to share the profits in the ratio of their investments. If their profit is ₹ 12000, how much does each get?

Answer:

Total investment = 15000 + 25000 = 40000
Investment of 1 st person = 15000/40000 = 3/8
Investment of 2nd person = 1 – (3/8) = 5/8
Total profit = ₹ 12000
Profit of 1st person = 3/8 × ₹12000 = ₹4500
Profit of 2nd person = ₹12000 – ₹4500 = ₹7500

Question 14. The ratio of Ankur’s money to Roma’s money is 9 : 11. if Ankur has ₹540, how much money does Roma have?

Answer:

Ratio of Ankur’s two Roma’s money = 9 : 11
Ankur has money = ₹540

Let Roma’s have = x
9 :11 :: 540 : x

(9/11) = (540/x)

x = (540 × 11)/9

x = ₹ 660

Question 15. The ratio of weights of tin and zinc in on alloy is 2 : 5. How much zinc is there in 31.5 g of alloy?

Answer:

Ratio of weight = 2 : 5
Sum of ratio = 2 + 5 = 7
Total weight of alloy =31.5g
Part of zinc = 31.5 × 5/7

= 315/10 = 5/7

= 45/2

= 22.5 g

—  : End of ML Aggarwal Ratio and Proportion Exe-8.1 Class 6 ICSE Maths Solutions :–

Return to –  ML Aggarwal Maths Solutions for ICSE Class -6

Thanks