Ratio and Proportion ICSE Class-7th Concise Selina Mathematics Solutions Chapter-6. We provide step by step Solutions of Exercise / lesson-6 Ratio and Proportion for ICSE Class-7 Concise Selina Mathematics. Our Solutions contain all type Questions with Exe-6 A and Exe-6 B, to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-7.
Ratio and Proportion ICSE Class-7th Concise Selina Mathematics Solutions Chapter-6
–: Select Topics :–
Exercise – 6 A
Ratio and Proportion ICSE Class-7th Concise Selina Mathematics
Question 1.
Express each of the given ratio in its simplest form :

Answer-1.
(i)
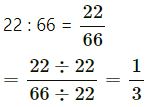
(HCF of 22 and 66 = 22)
= 1 : 3
(ii)
1.5 : 2.5 = 1.5/2.5 = 15/25
=(15÷5)/(25÷5)=3/5 (HCF of 15, 25 = 5)
= 3 : 5
(iii)
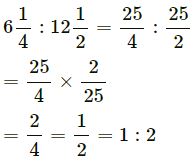
(iv)
40 kg : 1 quintal = 40 kg : 100 kg …(1 quintal = 100 kg)
= 40/100 = (40÷20)/(100÷20)
=25
(HCF of 40, 100 = 20)
= 2: 5
(v)
10 paise : ₹ 1 = 10 paise : 100 paise …(1 Rs. = 100 paise)
= 10/100 = 1/10
= 1:10
(vi)
200 m : 5 km = 200 m : 5000 m ….(1 km = 1000 m)
=200/5000= (200÷200)/(5000÷200)
..(HCF of 200, 5000 = 200)
=125
=1:25
(vii)
3 hours : 1 day = 3 hours : 24 hours …(1 day = 24 hours)
= 3/24
=1/8
=1:8
(viii)
6 months: 1 (1/3) years = 6 months : (4/3)×12 months
= 6 months : 16 months
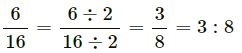
(ix)
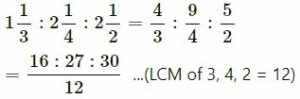
= 16: 27: 30
Question 2.
Divide 64 cm long string into two parts in the ratio 5 : 3.
Answer-2.
Sum of ratios = 5 + 3 = 8
∴ first part = 5/8 of 64 cm = 40 cm
Second part = 3/8 of 64 cm = 24 cm
Question-3.
Rs. 720 is divided between x and y in the ratio 4:5. How many rupees will each get?
Answer-3.
Total amount = Rs. 720 Ratio between x, y = 4 : 5
Sum of ratios = 4 + 5 = 9
x’s share = 4/9 of Rs. 720 = Rs. 320
y’s share = 5/9 of Rs. 720 = Rs. 400
Question-4.
The angles of a triangle are in the ratio 3 :2 : 7. Find each angle.
Answer-4.
Ratio in angles of a triangle = 3:2:7
Sum of ratios = 3 + 2 + 7=12
Sum of angles of a triangle = 180°
∴ First angle = (3/12)×180°=45°
Second angle = (2/12) x 180°= 30°
Third angle =(7/12) x 180°= 105°
Question-5.
A rectangular field is 100 m by 80 m. Find the ratio of
(i) length to its breadth
(ii) breadth to its perimeter.
Answer-5.
(i)
Length of field (l) = 100 m
Breadth (b) = 80 m
∴Perimeter = 2 (l + b) = 2 (100 + 80) m
= 2 x 180 = 360 m
Ratio between length and breadth
= 100 : 80 = 5 : 4
(Dividing by 20, the HCF of 100 and 80)
(ii)
Length of field (l) = 100 m
Breadth (b) = 80 m
∴Perimeter = 2 (l + b) = 2 (100 + 80) m
= 2 x 180 = 360 m
Ratio between breadth and its perimeter
= 80 : 360 = 2 : 9
(Dividing by 40, the HCF of 80 and 360)
Question-6.
The sum of three numbers, whose ratios are 3 : 4
: 6
is 4917.Find the numbers.
Answer-6.
Sum of three numbers = 4917
Ratio between them = 3(1/3) : 4(1/5) : 6(1/8)
= 10/3:21/5:49/8
= (400:504:735)/120 (LCM of 3, 5, 8 = 120)
= 400 : 504 : 735
Sum of ratio’s = 400 + 504 + 735 = 1639
∴ First number = 400/1639 of 4917 = 1200
Second number = 504/1639 of 4917 = 1512
and third number = 735/1639 of 4917 = 2205
The ratio between two quantities is 3 : the first is Rs. 810, find the second.
Answer-7.
Ratio between two quantities = 3 : 4
Sum of ratio = 3+4 = 7
∴ Second quantity = Rs. 810x/43
= Rs. 270 x 4 = Rs. 1080
Question-8.
Two numbers are in the ratio 5 : 7. Their difference is 10. Find the numbers.
Answer-8.
Ratio between two numbers = 5:7
Difference = 7-5 = 2
If difference is 2, then first number = 5
and if difference is 10, then first number
= (5/2)×10=25
and second number = (7/2)×10=35
Question-9.
Two numbers are in the ratio 10 : 11. Their sum is 168. Find the numbers.
Answer-9.
Ratio between two numbers = 10 : 11
Sum of ratios = 10 + 11=21
Total sum = 168
∴ First number = (168/21)×10=80
Second number = (168/21)×11=88
Question 10.
A line is divided in two parts in the ratio 2.5 : 1.3. If the smaller one is 35T cm, find the length of the line.
Answer-10.
Ratio between two parts of a line
= 2-5 : 1-3 =25 : 13
Sum of ratios = 25 + 13 = 38
Length of smaller part = 35.1 cm 38
Now length of line = (38/13)×35.1 cm
= 38 × 2.7 cm = 102.6 cm
Question-11.
In a class, the ratio of boys to the girls is 7:8. What part of the whole class are girls.
Answer-11
Ratio between boys and girls = 7:8
Sum of ratios = 7 + 8 = 15
∴ Girls are 8/15 of the whole class.
Question-12.
The population of a town is ’ 50,000, out of which males are of the whole population. Find the number of females. Also, find the ratio of the number of females to the whole population.
Answer-12
Total population = 180,000
Population of males = 1/3 of 180,000 = 60,000
∴ Population of females = 180,000 – 60,000 = 120,000
Ratio of females to whole population
= 120,000 : 180,000 = 2:3
Question-13.
Ten gram of an alloy of metals A and B contains 7.5 gm of metal A and the rest is metal B. Find the ratio between :
(i) the weights of metals A and B in the alloy.
(ii) the weight of metal B and the weight of the alloy.
Answer-13.
Total weight of A and B metals = 10 gm A’s weight = 7.5 gm B’s weight = 10 – 7.5 = 2.5 gm
(i) Ratio between A and B = 7.5 : 2.5
=75/10 : 25/10 = 3:1
(ii) Ratio between B and total alloy
= 2.5:10 = (25/10):10
⇒ 25 : 100 = 1 : 4
Question-14.
The ages of two boys A and B are 6 years 8 months and 7 years 4 months respectively. Divide Rs. 3,150 in the ratio of their ages.
Answer-14
A s age = 6 years 8 months
= 6 x 12 + 8 = 72 + 8 = 80 months
B’s age = 7 years 4 months = 7 x 12 + 4 = 84 + 4 = 88 months
∴ Ratio between them = 80 : 88 = 10 : 11
Amount = Rs. 3150
Sum of ratios = 10 + 11 =21
∴ A’s share = (3150×10)/21 = 1500 =
Rs. 1500
B’s share = (3150×11)/21=1650 =
Rs. 1650
Question-15.
Three persons start a business and spend Rs. 25,000; Rs. 15,000 and Rs. 40,000 respectively. Find the share of each out of a profit of Rs. 14,400 in a year.
Answer-15
A’s investment = Rs. 25000
B’s investment = Rs. 15000
C’s investment = Rs. 40000
∴ Ratio between their investment
= 25000 : 15000 : 40000
= 5 : 3 : 8
Sum of ratios = 5 + 3 + 8=16 Total profit = ₹ 14400
∴ A’s share = (14400/16)×5=₹4500
B’s share = (14400/16)×3 = ₹ 2700
C’s share = (14400/16)×8 = ₹ 7200
Question-16.
A plot of land, 600 sq m in area, is divided between two persons such that the first person gets three-fifth of what the second gets. Find the share of each.
Answer-16.
Area of plot of land = 600 sq. meter
Let second’s share = x
Then first share = (3/5)x
∴ Ratio between them (3/5)x:x
= (3/5):1 = 3:5
Sum of ratios = 3 + 5 = 8
∴ Share of first person = (600/8)×3 = 225 sq.m
and second share = (600/8)×5=375 sq.m.
Question-17.
Two poles of different heights are standing vertically on a horizontal field. At a particular time, the ratio between the lengths of their shadows is 2 :3. If the height of the smaller pole is 7.5 m, find the height of the other pole.
Answer-17.
Ratio between the shadows of two poles = 2:3
∴ Height of smaller pole = 7.5 m
Height of taller pole = (7.5×3)/2
= 22.5/2
=11.25
Question-18.
Two numbers are in the ratio 4 : 7. If their L.C.M. is 168, find the numbers.
Answer-18.
Given, Ratio in two numbers = 4:7
and their L.C.M. = 168
Let first number = 4x
and second number = 7x
Now, L.C.M. of 4x and 7x
= 4 x 7 x x = 28x
∴ 28x = 168
x = 168/28
x = 6
∴ Required numbers = 4x and 7x = 4 x 6 = 24
and 7 x 6 = 42
Question-19.
is divided between A and B in such a way that A gets half of B. Find :
(i) the ratio between the shares of A and B.
(ii) the share of A and the share of B.
Answer-19.
Total amount to be divided between A and B = ₹ 300
(i) A gets half of B
Hence, ratio between A and B = 1/2 = 1 :2
(ii) Sum of ratios = 1 + 2 = 3
∴ A’ shares = (300×1)/3=100
∴ B’ share = (300×2)/3=200
Question-20.
The ratio between two numbers is 5 : 9. Find the numbers, if their H.C.F. is 16.
Answer-20.
Let the first number be 5x and second number be 9x
H.C.F. of 5x and 9x = Largest number common to 5x and 9x = x
Given H.C.F. = 16 ⇒ x = 16
∴ Required numbers = 5x and 9x = 5×16 and 9×16 = 80 and 144
Question-21.
A bag contains ₹ 1,600 in the form of ₹10 and ₹20 notes. If the ratio between the numbers of ₹10 and ₹20 notes is 2 : 3; find the total number of notes in all.
Answer-21.
Total amount in the bag = 1600
It contains notes in the denomination of ₹10 and 20
Ratio between the number of ₹10 and 20 notes is = 2 : 3
Let number of ₹10 note = x
and number of ₹ 20 notes = y
According to condition,
10x + 20y = 1600 ….(i)
and x = 2/3y ….(ii)
Now, substitute the value of x in eq (i)
10×(2/3)y+20y=1600
⇒(20/3)y+20y=1600
⇒(20+60)/3 y=1600
⇒(80/3)y=1600
⇒ y = (1600×3)/80
∴ y = 60
Now, substitute the value of y in eq (ii), we get
x = 2/3 × 60=40
Total number of notes in all = x + y
= 60 + 40 = 100 notes
Question-22.
The ratio between the prices of a scooter and a refrigerator is 4 : 1. If the scooter costs ₹45,000 more than the refrigerator, find the price of the refrigerator.
Answer-22.
Ratio between the prices of scooter and a refrigerator = 4:1
Cost price of scooter = ₹45,000
Let the cost of scooter = 4x
Cost of refrigerator = 1x
According to condition,
Cost of scooter > Cost of refrigerator
⇒ 4x- 1x = 45000
⇒ 3x = 45000
x = 45000/3
⇒ x = 15000
∴ Price of refrigerator = ₹15000
Exercise – 6 B
Solutions of Ratio and Proportion for ICSE Class-7th Concise Selina Mathematics
Question-1.
Check whether the following quantities form a proportion or not ?

Answer-1.
(i)
3x, 7x, 24 and 56
If these are in proportion, then
3x × 56
= 7x × 24
⇒ 168 x
= 168 x
which is true.
Hence 3x, 7x, 24 and 56 are in proportion.
(ii)
0.8, 3, 2.4 and 9 are in proportion.
if 0.8 × 9
= 3 × 2.4
⇒ 7.2
= 7.2
which is true
Hence 0.8, 3, 2.4 and 9 are in proportion.
(iii)

(iv)
0.4, 0.5, 2.9 and 3.5 are in proportion
if 0.4 × 3.5
= 0.5 × 2.9
⇒ 1.40
= 1.45
which is not true
Hence 0.4, 0.5, 2.9
and 3.5 are not in proportion.
(v)

proportion.
Question-2.
Find the fourth proportional of

Answer-2.
(i)
Fourth proportional of 3, 12 and 4
(12 x 4)/3 = 16
(ii)
Fourth proportional of 5, 9 and 45
=(9×45)5
=81
(iii)
Fourth proportional of 2.1, 1.5 and 8.4
= (1.5×8.5)/2.1
=1.5×4=6.0
(iv)
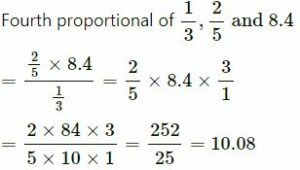
(v)
Fourth proportional of 4 hours 40 minutes, 1 hour 10 minutes and 16 hours.
4 hours 40 minutes = 4 × 60 + 40
= 240 40 = 280
1 hour 10 minutes = 1 × 60 + 10
= 60 + 10 = 70 minutes
16 hours = 16 × 60 = 960 minutes
∴ Fourth proportional = (70×960)/280
= 240 minutes = 240/60 = 4 hours
Question-3.
Find the third proportional of

Answer-3.
(i)
Third proportional of 27 and 9
(9 x 9)/27 = 3
(ii)
Third proportional to 2 m 40 cm and 40 cm or 240 cm and 40 cm
(40×40)/240
=203
=623 cm
(iii)
Third proportional to 1.8 and 0.6
= (0.6×0.6)/1.8
=0.36/1.8
=36180
=1/5
=0.2
(iv)
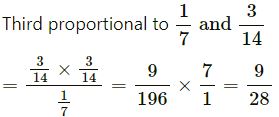
(v)
Third proportional to 1.6 and 0.8
= (0.8×0.8)/1.6
=0.64/1.6
= (64/160)
=25
=0.4
Question-4.
Find the mean proportional between

Answer-4.
(i)
Mean proportional between 16 and 4
![]()
(ii)
Mean proportional between 3 and 27
![]()
(iii)
Mean proportional between 0.9 and 2.5
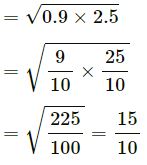
= 1.5
(iv)
Mean proportional between 0.6 and 9.6
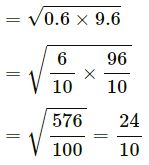
= 2.4
(v)
Mean proportional between 14 and 116
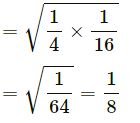
Question-5.
![]()

Answer-5.
(i)
A : B = 3 : 5
=3/5 : 1
(Dividing by 5)
and B : C = 4 : 7
= 1: 7/4 …
(Dividing by 4)
∴ A : B : C = 3/5 : 1 : 7/4
= 12 : 20 : 35 …
(Multiplying by 5 × 4 = 20)
(ii)
x : y = 2 : 3
= 2/3 : 1
(Dividing by 3)
and y : z = 5 : 7
=1 : 7/5 …
(Dividing by 5)
∴ x : y : z = 2/3 : 1 : 7/5
= 10 : 15 : 21 …
(Multiplying by 3 × 5 = 15)
(iii)
m : n = 4 : 9
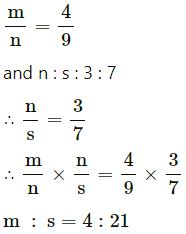
(iv)
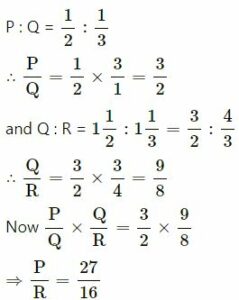
∴ P : R = 27 : 16
(v)
a : b = 1.5 : 3.5
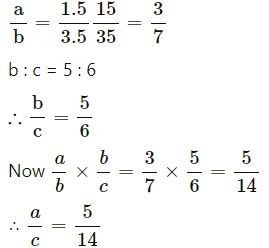
⇒ a : c = 5 : 14
(vi)

∴ p : r = 45 : 98
Question-6.
If x: y – 5 :4 and 2 : x = 3 :8, find the value of y.
Answer-6.
x : y = 5 : 4
and 2 : x = 3 : 8
Then, x/y=5/4 …(i)
and 2/x=3/8 …(ii)
x=(2×8)/3 = 16/3
Now put the value of x in eq. (i)
x/y=5/4
y = x ×(4/5)
y = (16/3)×(4/5)=64/15
Question-7.
Find the value of x, when 2.5 : 4 = x : 7.5.
Answer-7.
2.5 : 4 = x : 7.5
4 × x = 2.5 × 7.5
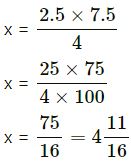
Question-8.
Show that 2, 12 and 72 are in continued proportion.
Answer-8.
Three numbers a, b and c are in continued
proportion if, a : b : : b : c
The numbers are 2, 12 and 72
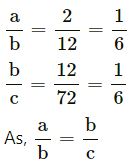
∴ 2, 12 and 72 are in continued proportion.
— End of Ratio and Proportion Solutions :–
Return to – Concise Selina Maths Solutions for ICSE Class -7
Thanks


