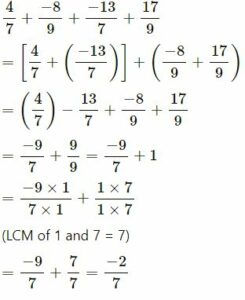Rational Numbers ICSE Class-8th Concise Selina Solutions Chapter-1. We provide step by step Solutions of Exercise / lesson-1 Rational Numbers for ICSE Class-8 Concise Selina Mathematics. Our Solutions contain all type Questions with Exe-1 A, Exe-1 B, Exe-1 C , Exe-1 D and Exe-1 E to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-8.
Rational Numbers ICSE Class-8th Concise Selina Solutions Chapter-1
–: Select Topics :–
Exercise – 1 A Rational Numbers ICSE Class-8th
Question -1.
Add, each pair of rational numbers, given below, and show that their addition (sum) is also a rational number:
(i) −5/8 and 3/8
(ii) −8/13 and −4/13
(iii) 6/11 and −9/11
(iv) 5/−26 and 8/39
(v) 5/−6 and 2/3
(vi) −2 and 2/5
(vii) 9/−4 and −3/8
(viii) 7/−18 and 8/27
Answer-1
(i) −5/8 and 3/8
= -5⁄8 + 3⁄8
(Denominators are same, LCM = 8)

Which is rational number
(LCM of 13 and 13 = 13)
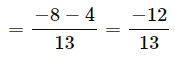
Which is rational number
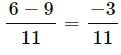
Which is a rational number

| 2 | 26, 39 |
| 3 | 13, 39 |
| 13 | 13, 13 |
| 1, 1 |
∴ LCM of 26 and 39 = 2 x 3 x 13 = 78
= -15+16⁄78 (LCM of 26 and 39 = 78)
= 1/78
Which is a rational number.
(v) 5/−6 and 2/3
= ..5⁄-6…+…2⁄3…
| 2 | 6, 3 |
| 3 | 3, 3 |
| 1, 1 |
LCM of 6, 3 = 2 x 3 = 6

Which is rational number.
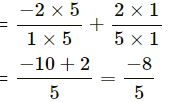
Which is a rational number
| 2 | 4, 8 |
| 2 | 2, 4 |
| 2 | 2, 2 |
| 1, 1 |
LCM of 4 and 8 = 2 x 2 x 2 = 8
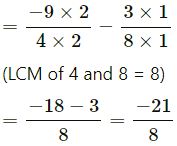
Which is a rational number
| 2 | 18, 27 |
| 3 | 9, 27 |
| 3 | 3, 9 |
| 3 | 1, 3 |
| 1, 1 |
LCM of 18 and 27 = 2 x 3 x 3 x 3 = 54
= -21 + 16⁄54=-5⁄54
Which is a rational number.
Question-2

Answer-2
(i) 5⁄9 + -7⁄6
| 2 | 9, 6 |
| 3 | 9, 3 |
| 3 | 3, 1 |
| 1, 1 |
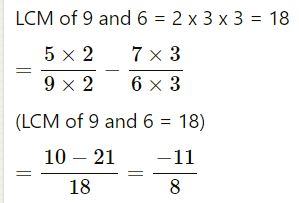
(ii) 4 + 3⁄-5
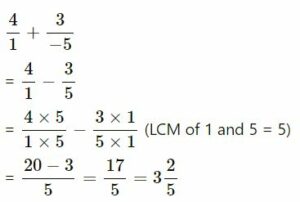
(iii)
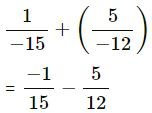
| 2 | 15, 12 |
| 2 | 15, 6 |
| 3 | 15, 3 |
| 5 | 5, 1 |
| 1, 1 |
LCM of 15 and 12 = 2 x 2 x 3 x 5 = 60
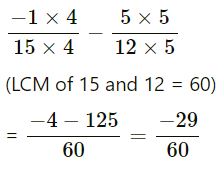
(iv) 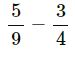
| 2 | 9, 4 |
| 2 | 9, 2 |
| 3 | 9, 1 |
| 3 | 3, 1 |
| 1,1 |
(LCM of 9 and 4 = 2 x 2 x 3 x 3 = 36)
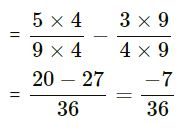
(LCM of 9 and 4 = 36)
= -7⁄36
(v) -8⁄9 + -5⁄12
| 2 | 9, 12 |
| 2 | 9, 6 |
| 3 | 9, 3 |
| 3 | 3, 1 |
| 1, 1 |
LCM of 9, 12 = 2 x 2 x 3 x 3 = 36

(vi) 0 + -2⁄7
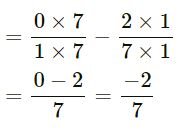
( LCM of 1 and 7 = 7 )
(vii) 5⁄-11 +0
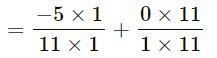
(LCM of 1 and 11 = 11)
= -5 + 0⁄11
= -5⁄11
(viii) 2 + -3⁄5
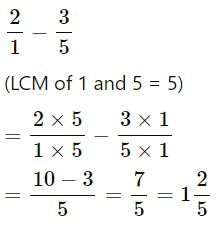
(ix) 4⁄-9 + 1
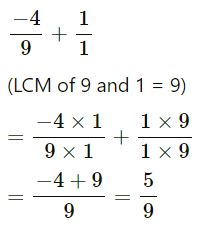
Question -3.
Evaluate:
(i) 3⁄7 + -4⁄9 + -11⁄7 + 7⁄9
(ii) 2⁄3 + -4⁄5+ 1⁄3+ 2⁄5
(iii) 4⁄7 +0 +-8⁄9 + -13/7 + 17⁄9
(iv) 3⁄8 + -5⁄12 + 3⁄7 + 3⁄12 + -5⁄8 + -2⁄7
Answer-3
(i) 3⁄7 + -4⁄9 + -11⁄7 + 7⁄9

| 3 | 7, 3 |
| 7 | 7,1 |
| 1,1 |
LCM of 3 and 2 = 3 x 7 = 21
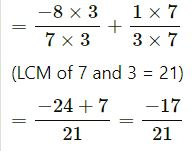
(ii) 2⁄3 + -4⁄5+ 1⁄3+ 2⁄5
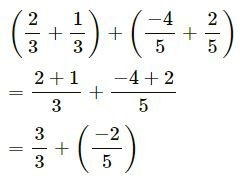
| 3 | 3, 5 |
| 5 | 1, 5 |
| 1, 1 |
LCM of 3 and 5 = 3 x 5 = 15
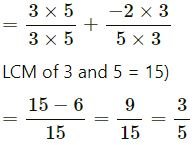
(iii) 4⁄7 +0 +-8⁄9 + -13/7 + 17⁄9
(iv) 3⁄8 + -5⁄12 + 3⁄7 + 3⁄12 + -5⁄8 + -2⁄7
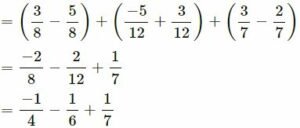
| 2 | 4, 6, 7 |
| 2 | 2, 3, 7 |
| 3 | 1, 3, 7 |
| 7 | 1, 1, 7 |
| 1, 1, 1 |
(LCM of 4, 6 and 7 = 2 x 2 x 3 x 7 = 84)
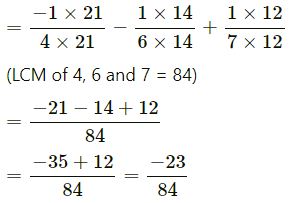
Question -4.
For each pair of rational numbers, verify commutative property of addition of rational numbers:
(i) -8⁄7 and 5⁄14
(ii) 5⁄9 and 5⁄-12
(iii) –4⁄5 and -13⁄-15
(iv) 2⁄-5 and 11⁄-15
(v) 3 and -2⁄7
(vi) −2 and 3⁄-5
Answer :-4
(i) -8⁄7 and 5⁄14
LCM of 7, 14 is 14
| 2 | 7, 14 |
| 7 | 7, 7 |
| 1, 1 |
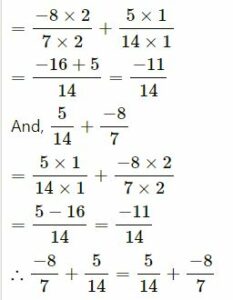
This verifies that commutative property for the addition of rational numbers.
(ii) 5⁄9 and 5⁄-12
LCM of 9, 12 is 36
| 2 | 9, 12 |
| 2 | 9, 6 |
| 3 | 9, 3 |
| 3 | 3, 1 |
| 1, 1 |

This verifies that commutative property for the addition of rational numbers.
(iii) –4⁄5 and -13⁄-15
LCM of 5, 15 is 15
| 5 | 5, 15 |
| 3 | 1, 3 |
| 1, 1 |
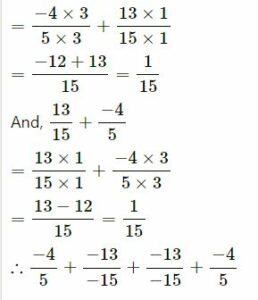
This verifies that commutative property for the addition of rational numbers.
(iv) 2⁄-5 and 11⁄-15
To prove: 2⁄-5+11⁄-15 =11⁄-15 +2⁄-5
LHS = 2⁄-5+11⁄-15
Taking LCM
3 5,15
5 5,5
1,1
∴LCM of 5 and 15=15

Hence, the commutative property for the addition of rational numbers is verified.
(v) 3 and −-2⁄7
To prove 3⁄1 + -2⁄7 = ..-2⁄7..+.. 3⁄1 .
LCM of 1 and 7=7)
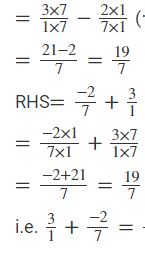
RHS = LHS
Hence, the commutative property for the addition of rational numbers is verified.
(vi) −2 and 3⁄-5
To prove: -2⁄1+− 3⁄-5=− 3⁄-5+2⁄1
∵(LCM of 1 and 5=5)
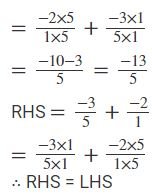
Hence, the commutative property for the addition of rational numbers is verified
Question -5.
For each set of rational numbers, given below, verify the associative property of addition of rational numbers:
(i) 1⁄2 , 2⁄3 and -1⁄6
(ii) -2⁄5 , 4⁄15 and -7⁄10
(iii) -7⁄9 , 2⁄3 and -5⁄18
(iv) -1 , 5⁄6 and -2⁄3
Answer-5
(i) 1⁄2 , 2⁄3 and -1⁄6
To prove:
… 1⁄2 + (2⁄3 + -1⁄6.)..= (.1⁄2 + 2⁄3 )+ -1⁄6 ….
LHS
1⁄2 + (2⁄3 + -1⁄6.)..
Taking LCM
2 3,6
3 3,3
1,1
∴LCM of 3 and 6=6

RHS = (.1⁄2 + 2⁄3 )+ -1⁄6 Taking LCM
2 2,3
3 1,3
1,1
∴ LCM of 2 and 3=6
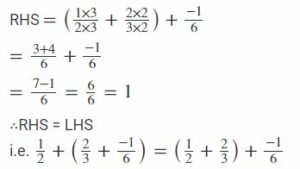
Hence, the associative property for the addition of rational numbers is verified.
(ii) -2⁄5 , 4⁄15 and -7⁄10
| 2 | 15 ,10 |
| 3 | 15 ,5 |
| 5 | 5 ,5 |
| 1 ,1 |
∴ LCM of 5, 15, 10 =2 x 3 x 5 = 30
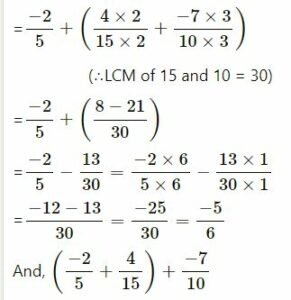
| 3 | 5, 15 |
| 5 | 5 ,5 |
| 1, 1 |
∴ LCM of 5 and 15 = 3 x 5 = 15

This verifies associative property of the addition of rational numbers.
(iii) -7⁄9 , 2⁄3 and -5⁄18
| 2 | 3, 18 |
| 3 | 3, 9 |
| 5 | 3, 3 |
| 1, 1 |
∴ LCM of 3 and 18 = 2 x 3 x 3 = 18

| 3 | 3, 9 |
| 3 | 3, 3 |
| 1, 1 |
∴ LCM of 3 and 9 = 3
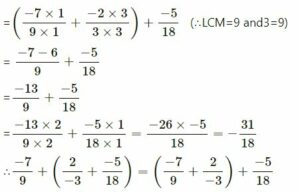
This verifies associative property of the addition of rational numbers.
(iv) -1 , 5⁄6 and -2⁄3
Show that :
This verifies associative property of the addition of rational numbers
….-1 + (5⁄6 + -2⁄3 )..=….(-1 + 5⁄6 )+ -2⁄3 ….
| 2 | 6, 3 |
| 3 | 3, 3 |
| 1, 1 |
LCM of 6 and 3 = 6

Write the additive inverse (negative) of:
(i) -3⁄8 ,
(ii) 4⁄-9 ,
(iii) -7⁄9 ,
(iv) -4⁄-13 ,
(v) 0,
(vi)-2
(vii) 1,
(viii) -1⁄3 ,
(ix) -3⁄1
Answer-6
we know that sum of number and its additive inverse=0
(i) -3⁄8 ,
The additive inverse of ….-3⁄8 , ..= …3⁄8 , …………
(ii) 4⁄-9 ,
The additive inverse of …-4⁄9 ..= …4⁄9 , …………
(iii) -7⁄9 ,
The additive inverse of -7⁄9 =7⁄9
(iv) -4⁄-13 ,
The additive inverse of -4⁄-13 , =4⁄-13 ,
(v) 0,
The additive inverse of 0=0
(vi)-2
The additive inverse of -2=2
(vii) 1,
The additive inverse of 1=-1
(viii) -1⁄3 ,
The additive inverse of -1⁄3 , =1⁄3 ,
(ix) -3⁄1
The additive inverse of -3⁄1=3
Question- 7.
Fill in the blanks:
i) Additive inverse of -5⁄-12=__________.
(ii) -5⁄-12+ its additive inverse =__________.
(iii) If a⁄b is additive inverse of -c⁄d then -c⁄d is additive inverse of __________.
Answer-7
i) Additive inverse of -5⁄-12=___-5⁄12_______.
(ii) -5⁄-12+ its additive inverse =__0________.
(iii) If a⁄b is additive inverse of -c⁄d then -c⁄d is additive inverse of _a⁄b_
Question -8.
State, true or false:
(i) 7⁄9= 7+5⁄9+5
(ii) 7⁄9= 7-5⁄9-5
(iii) 7⁄9= 7×5⁄9×5
(iv7⁄9= 7/5⁄9/5
(v) -5⁄-12 is a negative rational number
(vi) -13⁄25 smaller than -25⁄-13
Answer-8
(i) 7⁄9= 7+5⁄9+5
False
(ii) 7⁄9= 7-5⁄9-5
False
(iii) 7⁄9= 7×5⁄9×5
True
(iv7⁄9= 7/5⁄9/5
True
(v) -5⁄-12 is a negative rational number
False
(vi) -13⁄25 smaller than -25⁄-13
False
Exercise- 1 B Selina Concise Solutions Rational Numbers ICSE Class-8th
Question- 1.
Evaluate:
(i) 2/3−4/5
(ii) −4/9−2−3
(iii) −1−49
(iv) −27−3−14
(v) −518−−29
(vi) 521−−1342
Answer-1
Question -2.
Subtract:
Answer-2
Question- 3.
The sum of two rational numbers is 9/20. If one of them is 2/5, find the other.
Answer-3
Question -4.
The sum of the two rational numbers is -2/3. If one of them is -8/5, find the other.
Answer-4
Question- 5.
The sum of the two rational numbers is -6. If one of them is -8/5, find the other.
Answer-5
Question -6.
Which rational number should be added to -7/8 to get -5/9 ?
Answer-6
Question -7.
Which rational number should be added to -5/9 to get -2/3 ?
Answer-7
Question- 8.
Which rational number should be subtracted from -5/6 to get 4/9 ?
Answer-8
Question -9.
(i) What should be subtracted from -2 to get 3/8
(ii) What should be added to -2 to get 3/8
Answer-9
Question- 10.
Evaluate:
Answer-10
Exercise – 1 C Rational Numbers ICSE Class-8th Concise Selina Solutions
Question -1.
Evaluate:
Answer-1
Question- 2.
Multiply:
Answer-2
Question -3.
Evaluate:
Answer-3
Question -4.
Multiply each rational number, given below, by one (1):
Answer-4
Question- 5.
For each pair of rational numbers, given below, verify that the multiplication is commutative:
Answer-5
Question -6.
Write the reciprocal (multiplicative inverse) of each rational number, given below :
Answer-6
Question -7.
Find the reciprocal (multiplicative inverse) of:
Answer-7
Question- 8.
Answer-8
Question -9.
Answer-9
Question- 10.
Name the multiplication property of rational numbers shown below :
Answer-10
Question -11.
Fill in the blanks:
(i) The product of two positive rational numbers is always ……………
(ii) The product of two negative rational numbers is always ……………
(iii) If two rational numbers have opposite signs then their product is always …………..
(iv) The reciprocal of a positive rational number is ………. and the reciprocal of a negative rational number is ……………
(v) Rational number 0 has ………….. reciprocal.
(vi) The product of a rational number and its reciprocal is ………..
(vii) The numbers ……….. and ……….. are their own reciprocals.
(viii) If m is reciprocal of n, then the reciprocal of n is ………….
Answer-11
Exercise – 1 D Rational Numbers ICSE Class-8th
Question- 1.
Evaluate:
Answer-1
Question- 2.
Divide:
Answer-2
Question -3.
The product of two rational numbers is -2. If one of them is , find the other.
Answer-3
Question -4.
The product of two numbers is . If one of them is
, find the other.
Answer-4
Question -5.
m and n are two rational numbers such that
Answer-5
Question -6.
By what number must be multiplied so that the product is
?
Answer-6
Question -7.
By what number should be multiplied to get 16?
Answer-7
Question 8.
If 3 1/2 litres of milk costs ₹49, find the cost of one litre of milk?
Answer-8
Question -9.
Cost of 3 metre of cloth is ₹88
. What is the cost of 1 metre of cloth?
Answer-9
Question -10.
Divide the sum of and
by
.
Answer-11
Question 11.
Answer
Question 12.
The product of two rational numbers is -5. If one of these numbers is , find the other.
Answer
Question 13.
Divide the sum of and
by the difference of
and
Answer-13
Rational Numbers Exercise 1 E – Selina Concise Mathematics Class 8 ICSE Solutions
Question- 1.
Answer-1
Question -2.
Answer-2
Question -3.
Insert one rational number between (0 7 and 8 (ii) 3.5 and 5
(i) 2 and 3.2
(ii) 3.5 and 5
(iii) 2 and 3.2
(iv) 4.2 and 3.6
(v) and 2
Answer-3
Question- 4.
Insert two rational numbers between
(i) 6 and 7
(ii) 4.8 and 6
(iii) 2.7 and 6.3
Answer-4
Question -5.
Insert three rational numbers between
(i) 3 and 4
(ii) 10 and 12
Answer-5
Question -6.
Insert five rational numbers between and
Answer-6
Question -7.
Insert six rational numbers between and
Answer-7
Question -8.
Insert seven rational numbers between 2 and 3.
Answer-8
— End of Rational Numbers ICSE Class-8th Solutions :–
Return to – Concise Selina Maths Solutions for ICSE Class -8
Thanks