Reflection Class 10 OP Malhotra Exe-10B ICSE Maths Solutions Ch-10 Questions as latest prescribe guideline for upcoming exam. In this article you would learn Properties Related to Reflection. Visit official Website CISCE for detail information about ICSE Board Class-10 Mathematics.

Reflection Class 10 OP Malhotra Exe-10B ICSE Maths Solutions Ch-10
| Board | ICSE |
| Publications | S Chand |
| Subject | Maths |
| Class | 10th |
| Chapter-10 | Reflection |
| Writer | OP Malhotra |
| Exe-10B | Properties Related to Reflection |
| Edition | 2024-2025 |
Properties Related to Reflection
- Shape: The shape of the original figure and its mirror image are identical.
- Size: The size of the original figure and its mirror image are the same.
- Orientation: The orientation of the original figure and its mirror image are opposite.
- Distance: The distance between any point on the original figure and the line of reflection is the same as the distance between the corresponding point on the mirror image and the line of reflection.
- Angle: Angles between intersecting lines are the same in both the original figure and its mirror image.
Important Terms in Reflection
- Line of Reflection: The imaginary line across which a shape is reflected to create its mirror image. It is also known as the axis of reflection or mirror line.
- Mirror Image: The image formed when you reflect a shape across the line of reflection. It is identical to the original shape but appears reversed.
- Congruent Figures: Two figures that have the same size and shape. In reflection, the original shape and its mirror image are always congruent.
- Symmetry: The property of a shape or object that remains unchanged when reflected across a line, known as a line of symmetry.
INVARIANT POINT
Any point that remains unaltered under a given reflection is called an invariant point
Exercise- 10B
Reflection Class 10 OP Malhotra Exe-10B ICSE Maths Solutions Ch-10
Que-1: State the coordinates of
(a) Points (i) (5, 7), (ii) (3, -4), (iii) (-8, 9), (iv) (-1, -2) under reflection in the x-axis.
(b) Points (0 (2, 5), (ii) (1, -4), (iii) (-7, -13), (iv) (-6, 8) under reflection in’ the y-axis.
Sol: (a) Points (i) (5, 7), (ii) (3, -4), (iii) (-8, 9), (iv) (-1, -2) under reflection in the x-axis will be (i) (5, -7), (ii) (3, 4), (iii) (-8, -9) and (iv) (-1, 2)
(b) Points (i) (2, 5), (ii) (1, -4), (iii) (-7, – 13), (iv) (-6, 8) under reflection in the y-axis will be (i) (-2, 5), (ii) (-1, -4), (iii) (7, -13) and (iv) (6, 8)
Que-2: Parallelogram ABCD has vertices A (-3, 2), B (5, 2), C (7, -1), D (-1, -1). Determine the image A’, B’, C’, D’ of A, B, C, D respectively, under reflection in the x-axis.
Sol: The vertices of a parallelogram ABCD are A (-3, 2) B (5, 2), C (7, -1), D (-1, -1)
The image of these points in the x-axis will be A’ (-3, -2), B’ (5, -2), C’ (7, 1) and D’ (-1, 1)
Que-3: (i) Plot each of the given points on graph paper, reflect them in the x-axis and then reflect the points obtained in the y-axis. Write down the co-ordinates of the points obtained.
(a) (3, 4) (b) (-3, 2) (c) (5, 0) (d) (-3, -3)
(ii) What happens if you reflect first in the y-axis and then in the x-axis ?
Sol: (a) Reflection of the point A (3, 4) in x-axis will be (3, -4) and then in y-axis, will be (-3, -4).
(b) Similarly the refection of B (-3, 2) in x-axis will be (-3, 2) and then in y-axis will be (3, 2).
(c) Reflection of C (5, 0) in x-axis will be (5,0) and then in y-axis will be (-5, 0).

Que-4: A point P (a, b) is reflected in the y-axis to
P’ (-3, 5). Write down the values of a and b.
P” is the image of P, when reflected in the x-axis. Write down the coordinates of P”. Find the coordinates of P’”, when P is reflected in the line, parallel to the x-axis, such that its equation is y = -3.
Sol: A point P (a, b) is reflected in y-axis, the image is P’ (- a, b) but the reflection P’ is given (- 3, 5)
∴ Comparing, we get – a = – 3 ⇒ a = 3
and b = 5, then coordinates of P will be (3, 5)
∵ P” is the image of P when reflected in x-aixs the coordinate of P” will be (3, – 5)
Again P”‘ is the image of P when reflected in the line parallel to x-axis such that its equation isy
= – 3
Whose coordinates will be 2b – y where b = – 3 and y = 5
∴ 2b – y = 2 (- 3) – 5 = – 6 – 5 = – 11
and abscissa, x = 3
∴ Coordinates will be (3, -11)
Que-5: Use graph paper for this question.
(i) Plot the points P (2, -4). Use 1 cm = 1 unit on both the axes.
(ii) P’ is the image of P when reflected in AB, which is parallel to the x-axis and is at a distance 1 on the positive side of y-axis. (Le. the line y=1).
(iii) P” is the image of P’ when reflected in the line LM which is parallel to the y-axis is at a distance 1 on the negative side of the x-axis. (i.e., the line x = – 1).
Sol: (i) Point P (2, -4) is given.
(ii) The image of P’ when reflected to a line AB which is parallel to x-axis at a distance of 1 unit i.e. y= 1
∴ Co-ordinates of P’ will be (2, 2b – y) or [2, 2 x 1 – (- 4)]
or (2, 2 + 4), or (2, 6)
(iii) The co-ordinates of P”, which is the image of P’ when reflected in the line LM which is parallel to y-axis at a distance of 1 unit on the left side i.e. x = – 1
∴ Co-ordinates of P” will be (2a – x, y) or [2 x (-1) -2, 6], [(-2 -2), 6] or (-4, 6)
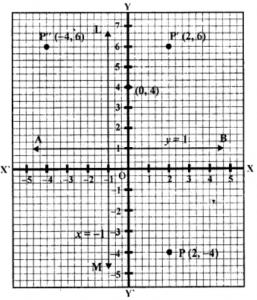
Que-6: A point P is reflected in the jr-axis. Co-ordinates of its image are (8, -6).
(i) Find the co-ordinates of P
(ii) Find the co-ordinates of the image of P under reflection in the .y-axis.
Sol: (i) Let P’ be the image of point P (x, y), whose co-ordinates are (8, -6) i.e. P’ (8, -6) when reflected in x-axis.
Co-ordinates of P will be (8, 6)
(ii) Let P” is the image of P when reflected iny-axis the co-ordinates of P” will be (-8, 6)
Que-7: The image of the point (1, 5) when reflected in a line LM is (9, 5). Write down the equation of the line LM.
Sol: Let P’ be the image of point P (1, 5) when reflected a line LM, is (9, 5)
Here we see the co-ordinates of y are same in P and P’
∴ The line LM is parallel to y-axis (x = 0)
i.e. equation of the line will be = 2a – x
⇒ 9 = 2a – 1 ⇒ 2a = 9 + 1 = 10
⇒ a = 5
Equation of the line parallel to y-axis will be x = a ⇒ x = 5
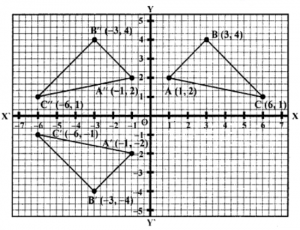
Que-8: Use graph paper to plot the triangle ABC where A is (1, 2), B is (3, 4) and C is (6,1). On the same graph paper plot.
(i) the image A, B, C of the triangle ABC under reflection in the origin O (0, 0);
(ii) the image of triangle ABC under reflection in the y-axis followed by a reflection in the x-axis.
Compare your results for (i) and (ii) above and make a statement connecting the two results.
Sol: Plot the points A (1, 2), B (3, 4) and C (6, 1) on the graph and join them to form a ∆ABC.
(i) The image of A, B and C under reflection in the origin are A’, B’ and C’ respectively and co-ordinate of A’, B’ and C’ will be A’ (-1, -2), B’ (-3, -4) and C’ (-6, -1) and are plotted on the graph as shown.
(ii) Under reflection of AABC in y-axis, the images of A, B and C will be A” (-1, 2), B” (-3,4) and C”(-6, 1)
And again under reflection it in the x-axis, we get the image of the ∆A”B”C” as ∆A’B’C’ which is the same as in (i).
(iii) So, we can say the results are same as in (i) and in (ii).
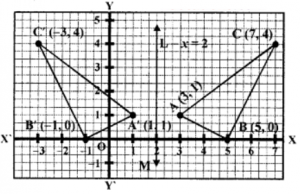
Que-9: On the graph paper, taking 1 cm = 1 unit, plot the triangle ABC whose vertices are at the points A (3, 1), B (5, 0) and C (7, 4). On the same diagram, draw the image of the AABC under reflection in the line x = 2. Mark I, the point invariant under this reflection.
Sol: Plot the vertices of ∆ABC whose vertices are A (3, 1), B (5, 0) and C (7, 4) .
Draw a line LM parallel to y-axis at a distance of 2 units on positive side which is x = 2 on reflection of AABC in the line x = 2, the image of A, B and C will be A’, B’ and C’ whose co-ordinates will be A’ (1, 1), B’ (-1, 0) and C’ (-3, 4) respectively.
Point is marked on the graph as the point in variant under this reflection whose co-ordinate are (2, 0).
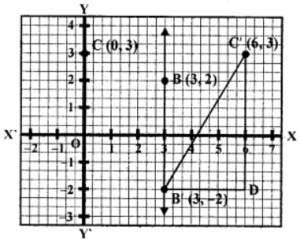
Que-10: B, C have co-ordinates (3, 2) and (0, 3). Find
(i) the image B’ of B under the reflection in the x-axis;
(ii) the image C’ of C under reflection in the line BB’;
(iii) Calculate the length of B’C’.
Sol: Plot the points B (3, 2) and C (0, 3) on the graph.
(i) The image B’ of B under reflection in the x-axis will be B’ (3, -2). Join BB’.
(ii) The image C’ (0, 3) of C under reflection in the line BB’ is C’ (6, 3).
(iii) Join B’C’. Draw perpendicular from C’ and B’ meeting each other at D.
Now C’D = 5 units and B’D = 3 units
∴ In right angled AC’B’D,
(B’C’)² = (B’D)² + (C’D)² (Pythagoras Theorem)
= (5)² + (3)² = 25 + 9 = 34
B’C’ = √34 units.
Que-11: The image of a point P under reflection in the x-axis is (5, -2). Write down the co-ordinates of P.
Sol: Let co-ordinates of P be (x, y), then
the image of P under reflection in the x-axis will be P’ (x, -y)
But P’ is given (5, -2)
Comparing, we get
x = 5, – y = – 2 ⇒ y = 2
∴Co-ordinates of P are (5, 2)
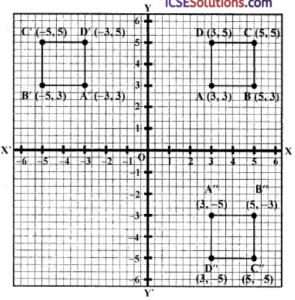
Que-12: Draw a square whose vertices are (3, 3), (5, 3), (5, 5) and (3, 5). Reflect the square in the y-axis and then reflect the image in the origin. What single transformation would give the same result ?
Sol: Plot the points A (3, 3), B (5, 3), C (5, 5), D (3, 5) and join AB, BC, CD and DA forming a square. Draw the image of A, B, C and D under reflection in, y-axis. The co-ordinates of images are A’ (-3, 3), B’ (-5, 3), C (-5, 5) and D’ (-3, 5)
Again reflect the points A’, B’, C’ and D’ in origin
The images are A” (3, -3), B” (5, -3), C” (5, -5) and D” (3, -5) respectively.
We see that reflection A”B”C”D” is the image of ABCD under reflection in x-axis.
Que-13: The triangle ABC, where A (1, 2), B (4, 8), C (6, 8), is reflected in the x-axis to triangle A’B’C’. Triangle A’B’C’ is then reflected in the origin to triangle A”B”C”. Write down the coordinates of A”, B”, C”. Write down a single transformation that maps ABC onto A”B”C”.
Sol: The vertices of a AABC are A (1,2), B (4, 8) and C (6, 8) and are reflected in the x-axis to AA’B’C’.
Then the co-ordinates of A’, B’ and C’ will be (1, -2), (4, -8) and (6, -8).
The ∆A’B’C’ is again reflected in the origin to AA”B”C”. Then the co-ordinates of A”, B” and C” will be (-1, 2), (-4, 8) and (-6, 8) We see that the single transformation of A”, B” and C” are the images of ∆ABC when reflected in y-axis.
Que-14: The point P (a, b) is first reflected in the origin, and then reflected in the y-axis to P’. If P’ has coordinates (3, -4), evaluate a, b.
Sol: Point P (a, b) is reflected under reflection in the origin
∴ Co-ordinates of the image of P will be P, (-a, -b)
Again P, (-a, -b) is reflected under reflection in the j-axis is to P’ whose co-ordinates will be (a, -b)
But co-ordinates of P’ are (3, – 4)
Then comparing, we get
a = 3, – b = – 4 ⇒ b = 4
∴ a = 3, b = 4
Que-15: The point P (-3, -2) on reflection in the x-axis is mapped as P’. Then P’ on reflection in the origin is mapped as P”. Find the coordinates of P’ and P”.
Sol: P’ is the image of point P (-3, -2) in the x-axis
∴ Co-ordinates of P’ will be (-3, 2)
P’ is again reflected under reflection in the origin to P”
Then the co-ordinates of P” will be (3, -2)
Que-16: Point A (5, -1) on reflection in the x-axis is mapped as A’. Also A on reflection in the 7-axis is mapped as A”. Write the co-ordinates of A’ and A”. Also calculate the distance AA”.
Sol: Point A (5, -1) is reflected in the x-axis to A’
Then co-ordinates of A’ will be (5, 1)
Point A (5, -1) is reflected in the 7-axis to A”
The co-ordinates of A” will be (- 5, – 1)
Length of AA” = √[(x1−x2)² + (y1−y2)²]
= √[(5−(−5))² + (−1−(−1))²]
= √[(10)2+(0)2] = √(100+0)
= √100
= 10 units
Que-17: Point A (2, – 4) is reflected in origin as A’. Point B (- 3, 2) is reflected in x-axis as B’. Write the coordinates of A’ and B’. Calculate the distance A’B’. Give your answer correct to 1 decimal place. (Do not consult tables)
Sol: Point A (2, – 4) is reflected in the origin to A’
Then co-ordinates of A’ will be (-2, 4)
Point B (-3, 2) is reflected in x-axis to B’
Then co-ordinates of B’ will be (-3, -2)
Now length of A’B’
= √[(x1−x2)²+(y1−y2)²]
= √[−2−(−3)]²+[4−(−2)]²
= √[(−2+3)²+(4+2)²]
= √[(1)²+(6)²] = √(1+36)
= √37 = 6.1 units
Que-18: Point A (4, -1) is reflected as A’ in the y- axis. Point B on reflection in the x-axis is mapped as B’ (-2, 5).
Write the coordinates of A’ and B.
Write the coordinates of the middle point of the line segment A’B.
Sol: Point A (4, -1) is reflected in y-axis as A’
∴ Co-ordinates of A’ will be (-4, -1)
Point B is reflected in x-axis as B’ (-2, 5)
Let co-ordinates of B’ be (x, y) then B’ will be (x, -y)
Comparing, we get
x = – 2, – y = 5 or x = – 2, y = – 5
∴ Co-ordinates of B are (- 2, – 5)
Let P (x1, y2) be the middle point of line segment A’B
∴ Co-ordinates of P will be
{(x1+x2)/2}, {(y1+y2)/2}
or {(−4−2)/}, {(−1−5)2}
or {(−6/2), (−6/2)} or (- 3, – 3)
Que-19: Point A (1, -5) is mapped as A’ on reflection in the x-axis. Point B (3, 2) is mapped as B’ on reflection in the origin. Write the coordinates of A’ and B’. Calculate AB’.
Sol: Point A(1, – 5) is mapped as A’ on reflection in the x-axis
∴ Co-ordinates of A’ will be (1, 5)
Point B (3, 2) is mapped as B’ on reflection in origin
∴ Co-ordinates of B’ will be (-3, -2)
Length of AB’ = √[1−(−3)]²+[−5−(−2)]²
= √[(1+3)²+(−5+2)]²
= √(16+9)
= √25 = 5
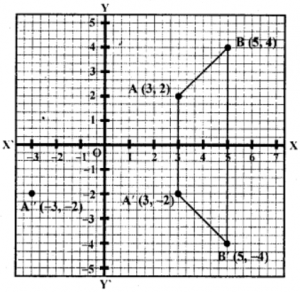
Que-20: Attempt this question on the graph paper.
(i) Plot A (3, 2) and B (5, 4) on the graph paper. Take 2 cm = 1 unit on both axes.
(ii) Reflect A and B in the x-axis to A’ and B’. Plot these on the same graph paper.
(iii) Write down
(a) the geometrical name of the figure ABBA’,
(b) the axis of symmetry of ABB’A,
(c) the measure of angle ABB’,
(d) the image of A” of A, when A is reflection in the origin,
(e) the single transformation that maps A’ onto A”.
Sol: (i) Plot the point A (3, 2) and B (5, 4) on the graph.
(ii) A’ and B’ are the reflection under reflection in x-axis
∴ Co-ordinates of A’ (3, -2) and of B (5, -4)
(iii) (a) Joining AB, BA’, A’B’ and B’A, the figure ABB’A’ is formed.
The figure so formed is of an isosceles trapezium.
(b) The axis of symmetry of the figure trapezium is the x-axis.
(c) The measure of ∠ABB’ is 45°.
(d) The A” is the image of A when reflected in origin.
The co-ordinates of A” will be (-3, -2).
(e) The single transformation that maps A’ onto A” is the reflection of A’ in y-axis.
–: End of Reflection Class 10 OP Malhotra Exe-10B ICSE Maths Solutions :–
Return to : OP Malhotra S Chand Solutions for ICSE Class-10 Maths
Thanks
Please Share with Your Friends


