Reflection Class 10 RS Aggarwal Exe-12B Goyal Brothers ICSE Maths Solutions Ch-12. Step by step solutions of exercise-12B questions as latest prescribe guideline for upcoming exam. Visit official Website CISCE for detail information about ICSE Board Class-10.
Reflection Class 10 RS Aggarwal Exe-12B Goyal Brothers ICSE Maths Solutions Ch-12
| Board | ICSE |
| Subject | Maths |
| Class | 10th |
| Chapter-12 | Reflection |
| Writer/ Book | RS Aggarwal |
| Exe-12B | Reflection of a Point Parallel to x/y axis |
| Academic Session | 2024-2025 |
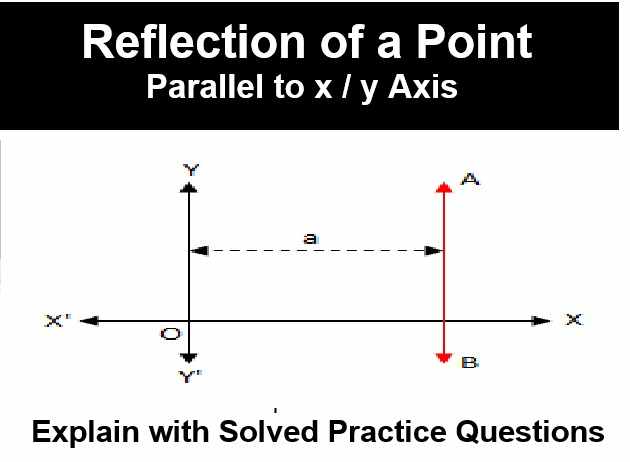
Reflection of a point parallel to x axes
Let P be a point whose coordinates are (x, y), AB be a line parallel the x-axis and the distance of AB from the x-axis be a. Let the image of P be P’ in the line AB
Clearly, P’ will be similarly situated on that side of AB which is opposite to P. So, the y-coordinates of P’ will be -y + 2a while the x-coordinate will be the same as that of P.
The image of the point (x, y) in the line parallel to the x-axis at a distance form the x-axis (i.e., y = a) is the point(x, -y + 2a), where a is taken positive if the line is on the positive side of the y-axis and a is taken negative if the line is on the negative side of the y-axis
Reflection of a point parallel to Y axes
Let P be a point whose coordinates are (x, y), AB be a line parallel the y-axis and the distance of AB from the y-axis be a. Let the image of P be P’ in the line AB
Clearly, P’ will be similarly situated on that side of AB which is opposite to P. So, the y-coordinates of P’ will be –x + 2a while the y-coordinate will be the same as that of P.
The image of the point (x, y) in the line parallel to the y-axis at a distance from the y-axis (i.e., x = a) is the point (-x + 2a, y), where a is taken positive if the line is on the positive side of the x-axis and a is taken negative if the line is on the negative side of the x-axis.
Exercise- 12B
( Reflection Class 10 RS Aggarwal Exe-12B Goyal Brothers ICSE Maths Solutions Ch-12)
Que-1: Find the image of each of the following points under reflection in x-axis :
(i) (6,3) (ii) (7,-5) (iii) (-4,3) (iv) (-2,-4) (v) (0,3)
Sol: The image of the following points under reflection in x-axis is:
(i) (6,-3)
(ii) (7,5
(iii) (-4,-3)
(iv) (-2,4)
(v) (0,-3)
Que-2: Find the image of each of the following points under reflection in y-axis :
(i) (2,6) (ii) (-3,8) (iii) (-5,-3) (iv) (0,-1) (v) (4,0)
Sol: The image of the following points under reflection in y-axis is:
(i) (-2,6)
(ii) (3,8)
(iii) (5,-3)
(iv) (0,-1)
(v) (-4,0)
Que-3: Find the image of each of the following points under reflection in the origin :
(i) (-5,8) (ii) (-6,-4) (iii) (7,4) (iv) (9,0) (v) (0,7)
Sol: The image of the following points under reflection in origin is:
(i) (5,-8)
(ii) (6,4)
(iii) (-7,-4)
(iv) (-9,0)
(v) (0,-7)
Que-4: Find the image of each of the following points under reflection in the line x = 0 :
(i) (4,7) (ii) (-3,-5) (iii) (-8,6) (iv) (5,0) (vi) (0,-2)
Sol: Image of the following points in the line x = 0, i.e., y-axis
(i) (-4,7)
(ii) (3,-5)
(iii) (8,6)
(iv) (-5,0)
(v) (0,-2)
Que-5: Find the image of each of the following points under reflection in the line y = 0 :
(i) (6,-7) (ii) (-8,4) (iii) (-3,-8) (iv) (7,9) (v) (0,-6)
Sol: Image of the following points under reflection in the line y = 0, i.e., x-axis
(i) (6,7)
(ii) (-8,-4)
(iii) (-3,8)
(iv) (7,-9)
(v) (0,6)
Que-6: The point P(-6,-3) on reflection in y-axis mapped on P’. The point P’ on reflection in the origin is mapped on P”.
(i) Find the co-ordinates of P’ (ii) Find the co-ordinates of P” (iii) Write down a single transformation that maps P onto P”.
Sol: (i) P’ is the image of the point P in y-axis
Point P(-6,-3) reflected on y-axis
So, P'(6,-3).
(ii) P” is the image of the point P’ in origin
Point P'(6,-3) reflected on origin
So, P”(-6,3).
(iii) From (i) and (ii), we get,
The single transformation that maps P onto P” is reflection in x-axis.
Que-7: The point P(4,-7) is reflected in the origin to the point P’. The point P’ is then reflected in x-axis to the point P”.
(i) Find the co-ordinates of P’ (ii) Find the co-ordinates of P” (iii) Write down a single transformation that maps P onto P”.
Sol: (i) P’ is the image of the point P in origin
Point P(4,-7) reflected on origin
So, P'(-4,7)
(ii) P” is the image of the point P’ in x-axis
Point P'(-4,7) reflected on origin
So, P”(-4,-7).
(iii) From (i) and (ii)
The single transforming that maps P onto P” is reflection in y-axis.
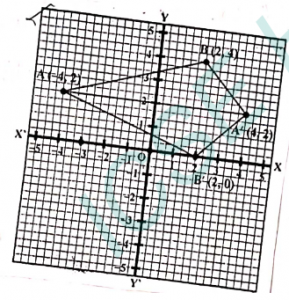
Que-8: (i) The vertices of a ΔABC are A(2,-3), B(-1,2) and C(3,0). This triangle is reflected in x-axis to form ΔA’B’C’. Find the co-ordinates A’, B’, C’. Are the two triangles congruent ?
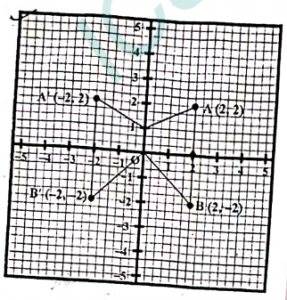
(ii) The point P(-2,4), Q(-3,1) and R(6,2) are the vertices of a triangle. ΔPQR is reflected in y-axis to form ΔP’Q’R’. Find the co-ordinates of P’, Q’ and R’
Sol: (i)

From graph we get,
AB = A’B’
AC = A’C’
BC = B’C’
Hence, △ABC and △A’B’C’ are congruent.
(ii) ΔPQR is reflected in y-axis and the co-ordinates are P(-2,4), Q(3,-1) and R(6,2).
P’, Q’ and R’ are image of the point P, Q and R respectively in y-axis.
Co-ordinates of P’, the image of P(-2,4) will be P'(2,4)
The co-ordinates of Q’ is the image of Q(3,-1) will be (-3,-1) and the co-ordinate of R’ is the image of R(6,2) will be (-6,2)
Que-9: Use a graph paper for this question (Take 2cm = 1 unit on both x and y axis)
(i) Plot the following points : A(0,4), B(2,3), C(1,1) and D(2,0)
(ii) Reflect points B, C, D on the y-axis and write down their coordinates. Name the images as B’, C’, D’ respectively.
(iii) Join the points A, B, C, D, B’, C’, D, and A in order, so as to form a closed figure. Write down the equation of the line of symmetry of the figure formed.
Sol: (i)
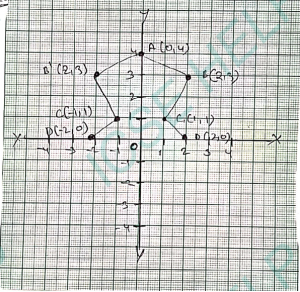
(ii) B'(-2,3), C'(-1,1) and D'(-2,0)
(iii) ABCDD’C’B’ is the required figure.
Line of symmetry is the y-axis.
Its equation is x = 0.
Que-10: (i) Plot the point A(3,2) and B(5,4) on a graph.
(ii) Reflect A and B in x-axis to A’ and B’ respectively. Plot A’ and B’ on the same graph paper. Write down the co-ordinates of A’ and B’.
(iii) Write down :
(a) the geometrical name of the figure ABB’A’.
(b) m ∠ABB’
(c) the image A” of A when reflected in the origin.
(d) the single transformation that maps A’ to A”.
Sol: (i) The point A(3,2) and B(5,4) have been plotted on a graph.
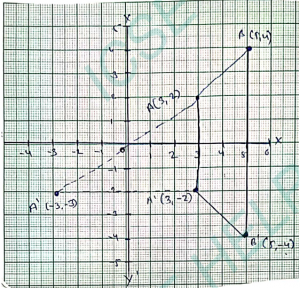
(ii) A’ and B’ are the image of A and B respectively is x-axis
Co-ordinate of A'(3,-2) and of B'(5,-4) respectively.
(iii) (a) By joining them in order, the figure ABB’A’ is formed is a trapezium.
(b) Let AL ⊥ BB’ (AL = BB’ = 2 units)
ΔALB is isosceles right angle triangle
∠ABB’ = 45°
(c) A’ is the image of A in origin and its co-ordinate are A'(-3,-2).
(d) The single transformation that maps A’ to A” to y-axis.
Que-11: Points P and Q have coordinates (0,5) and (-2,4).
(i) P is invariant when reflected in an axis. Name the axis.
(ii) Find the image of Q on reflection in the axis found in (i).
(iii) (0,k) on reflection in the origin is invariant. Write the value of k.
(iv) Write down the co-ordinates of the image Q, obtained by reflecting it in the origin followed by reflection in the x-axis.
Sol:
i . Any point that remains unaltered under a given transformation is called an invariant. It is given that P (0, 5) is invariant when reflected in an axis. Clearly, when P is reflected in the y-axis then it will remain invariant. Thus, the required axis is the y-axis.
ii. The co-ordinates of the image of Q (–2, 4) when reflected in y-axis is (2, 4).
iii. (0, k) on reflection in the origin is invariant. We know the reflection of origin in origin is invariant. Thus, k = 0.
iv. Co-ordinates of image of Q (–2, 4) when reflected in origin = (2, –4) Co-ordinates of image of (2, –4) when reflected in x-axis = (2, 4)
Thus, the co-ordinates of the point are (2, 4).
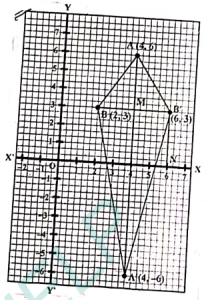
Que-12: Use a graph paper for this question. Plot the points P(3,2) and Q(-3,-2). From P and Q draw perpendiculars PM and QN on the x-axis.
(i) Name the image of P on reflection in the origin.
(ii) Assign the special name to the geometrical figure PQMN and find its area.
(iii) Write down the co-ordinates of the point to which M is mapped on reflection in (a) x-axis (b) y-axis (c) origin.
Sol: In the graph paper
(i) Q (-3, -2)
(ii) Parallelogram;
Area of ΔPMN = PM x MN x (1 / 2)
= 1/2× (2×63)
∴ Area of PMQN
= 2 x ΔPMN
= 2 x 6
= 12 square unit
(iii) Co-ordinates of M(3, 0)
(i) (3, 0), (ii) (-3, 0), (iii) (-3, 0).
Que-13: The point P(3,4) is reflected to P’ in x-axis and O’ is the image of O (origin) when reflected in the line PP’. Using graph paper, give :
(i) the coordinates of P’ and O’
(ii) the length of the segments PP’ and OO’.
(iii) the geometrical name of the figure POP’O’
(iv) the perimeter of the quadrilateral POP’O’.
Sol:
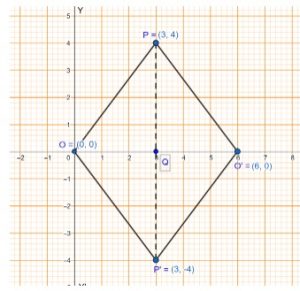
(i) From graph we get,
The coordinates of P’ and O’ are (3, -4) and (6, 0) respectively.
(ii) From graph we get,
Length of PP’ = 8 units and OO’ = 6 units
∴ Perimeter of POP’O’ is = 4 × OP
= 4 × 5 units = 20 units
iv. Quadrilateral POP’O’ is a rhombus.
Que-14: Use a graph paper for this question. A(1,1), B(5,1), C(4,2) and D(2,2) are the vertices of a quadrilateral.
(i) Name the quadrilateral ABCD
(ii) A, B, C, D are reflected in the origin onto A’, B’, C’ and D’ respectively. Locate A’, B’, C’, D’ on the graph paper and write their co-ordinates.
(iii) Are D, A, A’ and D’ collinear?
Sol: (i) Quadrilateral ABCD is an isosceles trapezium.
(ii) Co-ordinates of A’, B’, C’ and D’ are A'(–1, –1), B'(–5, –1), C'(–4, –2) and D'(–2, –2) respectively.
(iii) It is clear from the graph that D, A, A’ and D’ are collinear.
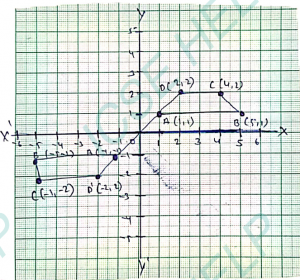
Que-15: A ΔABC with vertices A(1,2), B(4,4) and C(3,7) is the first reflected in the line y = 0 onto ΔA’B’C’ and then ΔA’B’C’ is reflected in the origin onto ΔA”B”C”.
Write down the co-ordinates of : (i) A’, B’ and C’ (ii) A”, B” and C” Write down the single transformation that maps ΔABC directly onto ΔA”B”C”.
Sol: Vertices of ΔABC are A(1,2), B(4,4) and C(3,7) is reflected first in the line y=0.
i.e., x-axis then the image of A, B and C of the figure will be A’, B’ and C’.
(i) A'(1,-2), B(4,-4) and C'(3,-7)
(ii) Then A’B’C’ is reflected in the origin onto ΔA”B”C”
The coordinate of A”, B” and C” will be A”(-1,2), B”(-4,4) and C”(-3,7).
(iii) ΔABC maps directly on A”B”C” in the y-axis.
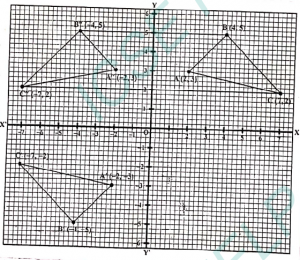
Que-16: Use graph paper for this question.
The points A(2,3), B(4,5) and C(7,2) are the vertices of ΔABC
(i) Write down the coordinates A’, B, ‘C’, if ΔA’B’C’ is the image of the ΔABC, when reflected in the origin
(ii) Write down the coordinates of A”, B”, C”, if ΔA”B”C” is the image of the ΔABC, when reflected in the x-axis.
(iii) Mention the special name of the quadrilateral BCC”B” and find its area.
Sol: (i) Reflection in origin
(x,y)→M = (−x,−y)
∴ A(2,3)→M = A′(−2,−3)
B(4,5)→M = B′(−4,−5)
C(7,2)→M = C′(−7,−2)
(ii) Now A, B, C is reflected in X axis.
Reflection in X axis
(x,y)→Mx = (x,−y)
∴ A(2,3)→Mx = A”(2,−3)
B(4,5)→Mx = B”(4,−5)
C(7,2)→Mx = C”(7,−2)
(iii) BCC”B” is an isosceles trapezium.
CD = 7 – 4 = 3
CC” = 2 + 2 = 4 and
BB” = 5 + 5 = 10
Area of Trapezium = (1/2) (CC” + BB”) x CD
= (1/2) (4 + 10) x 3
= (1/2) x 14 x 3
= 21 sq. unit.
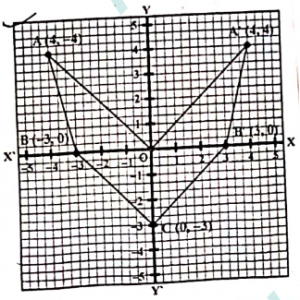
Que-17: Use graph paper taking 2cm = 1 unit along both axes.
Plot the points O(0,0), A(-4,4), B(-3,0) and C(0,-3)
(i) Reflects point A and B on y-axis and name them A’ and B’ respectively. Write down their co-ordinates.
(ii) Name the figure OABCB’A’.
(iii) State the line of symmetry of this figure.
Sol: (i) A’ = (4, 4) AND B’ = (3, 0)
(ii) The figure is an arrowhead
(iii) The y-axis is the line of symmetry of figure OABCB’A’.
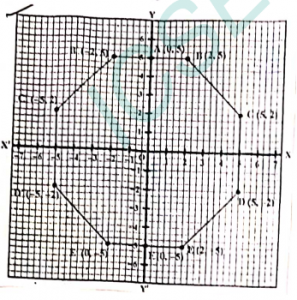
Que-18: Use a graph for this question taking 1cm = 1 unit along both x and y axis.
(i) Plot the points A(0,5), B(2,5), C(5,2), D(5,-2), E(2,-5) and F(0,-5).
(ii) Reflect the points B, C, D, and E on y-axis and name them respectively as B’, C’, D’ and E’
(iii) Write the co-ordinates of B’, C’, D’ and E’
(iv) Name the figure formed by BCDEE’D’C’B’.
(v) Name a line of symmetry for the figure formed.
Sol: (i) See the figure
(ii) Reflection of points on the y-axis will result in the change of the x-coordinate
(iii) Points will be B’(−2, 5), C’(−5, 2), D’(−5, −2), E’(−2, −5).
(iv) The figure BCDEE’D’C’B’ is a hexagon
(v) The lines of symmetry are x-axis or y-axis.
Que-19: Use graph paper to answer the following questions. (take 2cm = 1 unit)
(i) Plot the points A(-4,2) and B(2,4)
(ii) A’ is the image of A when reflected in the y-axis. Plot it on the graph paper and write the co-ordinates of A’
(iii) B’ is the image of B when reflected in the line AA’. Write the co-ordinates of B’.
(iv) Write the geometric name of the figure ABA’B’
(v) Name a line of symmetry of the figure formed.
Sol: (i) On the graph.
(ii) Co-ordinates of A’ = (4, 2).
(iii) Co-ordinates of B’ = (2, 0).
(iv) Geometric name of Fig. ABA’B’ is kite.
(v) Line of symmetry = AA’.
Que-20: Use graph paper for this question (Take 2cm = 1 unit along both x and y axis.) ABCD is a quadrilateral whose vertices are A(2,2), B(2,-2), C(0,-1) and D(0,1)
(i) Reflect quadrilateral ABCD on y-axis and name it as A’B’CD.
(ii) Write down the co-ordinates of A’ and B’
(iii) Name two points which are invariant under the above reflection.
(iv) Name the polygon A’B’CD.
Sol: (i) A'(-2,2) and B'(-2,-2)
(iii) C and D
(iv) Isosceles trapezium.
Que-21: Find the image of the following points as directed.
(i) Point A(4,5) reflected in the line x = 6
(ii) Point B(-3,2) reflected in the line x = -5
(iii) Point C(3,6) reflected in the line y = -2
(iv) Point D(-2,-5) reflected in the line y = 5.
Sol: The image of point (a,b) in the line x = c(x-a, b)
(i) A(4,5) reflected in the line x = 6.
(2×6-4, 5) i.e., A’ (-8,5).
(ii) B(-3,2) reflected in the line x = -5.
(2×-5-(-3), 2) i.e., A’ (-7,2).
(ii) We know that image point (a,b) in the line y = d be (a, 2d-b)
Image of point C(3,6) reflected in the line y = -2 be
[3, 2×(-2)-6] i.e., C’ = (3,-10).
(iv) Image of point D(-2,-5) reflected in the line y = 5 be
[-2, 2×5-(-5)] i.e., D’ = (-2,15).
Que-22: On a graph, plot A(4,6) and B(2,3). Find the image of A when reflected in the line y = 0, name it A’. Find the co-ordinates of B’ the image of B when reflected in the line AA’.
Give a geometrical name for the figure AB’A’B. Calculate the area of the figure AB’A’B.
Sol: The image of point A(4,6) when reflected in x-axis is the point A'(4,-6)
The equation of the line AA’ is x = 4.
Let BB’ cut AA’ at M then BM = 2 units.
Produce BM to B’ such that MB’ = BM = 2 units
Draw B’N ⊥ X’OX, Clearly ON = 6 units.
So, the coordinate of B’ are (6,3)
Figure ABA’B is a kite
Diagonal AA’ = 12 sq. units
and diagonal BB’ = 4 sq. units
area of kite = (AA’×BB’)/2
= (12×4)/2
= 24 sq. units.
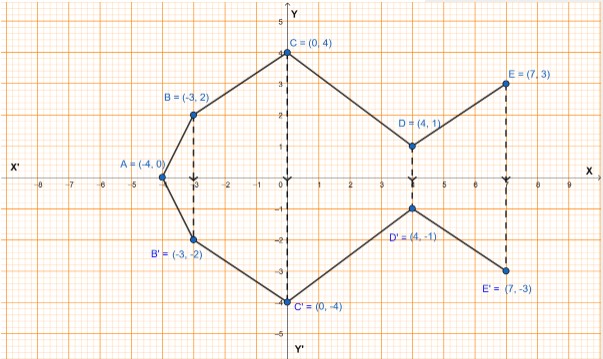
Que-23: Use graph paper for this question.
Take 1cm = 1 unit on both x and y axes.
(i) Plot the following points on your graph sheets :
A(-4,0), B(-3,2), C(0,4), D(4,1) and E(7,3)
(ii) Reflect the point B, C, D and E on the x-axis and name them as B’, C’, D’ and E’ respectively.
(iii) Join the points A, B, C, D, E, E’, D’ and A in order.
(iv) Name the closed figure formed.
Sol:
Que-24: Use a graph paper for this question. Take 2cm = 1 unit along both the axes.
(i) Plot the points A(0,4), B(2,2), C(5,2) and D(4,0), E(0,0) is the origin.
(ii) Reflect B, C, D on the y-axis and name them as B’, C’ and D’ respectively.
(iii) Join the points ABCD D’ C’ B’ and A in order and give a geometrical name to the closed figure.
Sol: update soon
— : Reflection Class 10 RS Aggarwal Exe-12B Goyal Brothers ICSE Maths Solutions :–
Return to: ICSE Class 10 Maths RS Aggarwal Solutions
Please share with your friend
Thanks


