Refraction and Dispersion of Light through a Prism Numerical Class-12 Nootan ISC Physics Solution Ch-17. Step by step solutions of Kumar and Mittal Physics of Nageen Prakashan as council latest prescribe guideline for upcoming exam. Visit official Website CISCE for detail information about ISC Board Class-12 Physics.
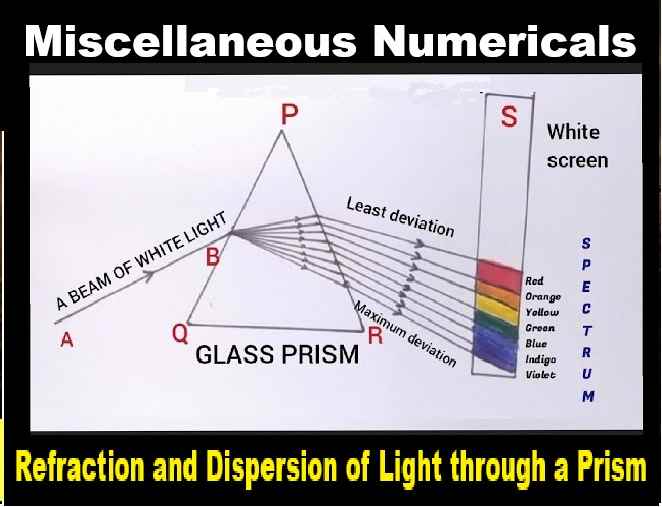
Refraction and Dispersion of Light through a Prism Numerical Class-12 Nootan ISC Physics Solution Ch-17
| Board | ISC |
| Class | 12 |
| Subject | Physics |
| Book | Nootan |
| Chapter-17 | Refraction and Dispersion of Light through a Prism |
| Topics | Miscellaneous Numericals With Solutions |
| Academic Session | 2025-2026 |
Miscellaneous Numericals With Solutions
Refraction and Dispersion of Light through a Prism Class-12 Nootan ISC Physics Solution Ch-17.
Que-22: A glass prism whose refracting angle is 72° and refractive index 1.66 is kept in a liquid of refractive index 1.33. Calculate the angle of minimum deviation for the parallel beam passing through the prism. (Given: sin 36° = 0.5878, sin 47.2° = 0.7336)
Ans- lug = ug/ul
=> 1.66/1.33 = 1.25
again μ = [sin (A+δm / 2)] / sin (A/2)
=> 1.25 = [sin (A+δm / 2)] / sin 36°
=> [sin (A+δm / 2)] = 1.25 x 0.588 = sin 47.3°
=> A + δm = 94.4
∴ δm = 94.6 – 72 = 22.4
Que-23: A parallel beam of light is incident on a face of a 60° prism. By rotating the prism, the minimum angle of deviation is measured to be 40°. Find the refractive index of the prism material. If the prism is placed in water (refractive index 1.33), then what would be the new minimum angle of deviation?
Ans- A = 60° , δm = 40°
n = [sin (60°+ 40°) / 2] / sin (60° /2)
=> n = 0.766/0.5
=> n = 1.532
now,
=> 1.152 = [sin (60° + δm) / 2] / sin (30°)
=> 1.152 x 0.5 = sin (60°+ δm) / 2
=> sin^-1(0.576) = (60°+δm) / 2
=> δm = 10°
— : End of Refraction and Dispersion of Light through a Prism Numerical Class-12 Nootan ISC Physics Solution Ch-17.:–
Return to : – Nootan Solutions for ISC Class-12 Physics
Thanks


