Relations and Functions Class 11 OP Malhotra Exe-2C ISC Maths Solutions Ch-2 Solutions. In this article you would learn about Domain, Range and Image of Function. Step by step solutions of latest textbook has been given as latest syllabus. Visit official Website CISCE for detail information about ISC Board Class-11 Mathematics.

Relations and Functions Class 11 OP Malhotra Exe-2C ISC Maths Solutions Ch-2
| Board | ISC |
| Publications | S Chand |
| Subject | Maths |
| Class | 11th |
| Chapter-2 | Relations and Functions |
| Writer | OP Malhotra |
| Exe-2(C) | Domain, Range and Image of Function. |
Exercise- 2C
Relations and Functions Class 11 OP Malhotra Exe-2C Solution.
Que-1: Let A = {1, 2, 3, 4}, B = {1, 5, 9, 11, 15, 16} and f = {(1,5), (2,9), (3,1), (4,5), (2,11)}. Are the following true ?
(i) f is a relation from A to B
(ii) f is a function from A to B.
Justify your answer in each case.
Sol: It is given that
A = {1, 2, 3, 4}, B = {1, 5, 9, 11, 15, 16} and f = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}.
Therefore,
A x B = {(1, 1), (1, 5), (1, 9), (1,11), (1, 15), (1, 16), (2, 1), (2, 5), (2, 9),
(2, 11), (2, 15), (2, 16), (3, 1), (3, 5), (3, 9), (3, 11), (3, 15),
(3, 16), (4, 1), (4, 5), (4, 9), (4, 11), (4, 15), (4, 16)}
(i) A relation from a non-empty set A to a non-empty set B is a subset of the Cartesian product A x B .
It is observed that f is a subset of A x B.
Thus, f is a relation from A to B.
(ii) Since the same first element
i.e., 2 corresponds to two different images i.e., 9 and 11.
Thus, f is not a function from A to B
Que-2: Let X = {1, 2, 3, 4}. Determine whether or not each relation is a function from X into X.
(i) f = {(2, 3), (1, 4), (2, 1), (3, 2), (4, 4)}
(ii) g = {(3, 1), (4, 2), (1, 1)}
(iii) h = {(2, 1), (3, 4), (1, 4), (4, 4)}
Sol: Given X = {1, 2, 3, 4}
(i) Given relation f = {(2, 3), (1, 4), (2, 1), (3, 2), (4, 4)}
Since element 2 ∈ X has two images 1 and 3
∴ each element of X does not have unique image.
Hence f is not a function.
(ii) Given relation g = {(3, 1), (4, 2), (1, 1)}
Clearly each element of X has unique image in x under relation g. Thus relation g is a function.
(iii) Given h = {(2, 1), (3, 4), (1, 4), (4, 4)}
Clearly each element of X has unique image in X. ∴ relation h is a function.
Que-3: State for each of the following relations whether it is function or not. (Write Yes or No)
(i) {(1, 2), (2, 2), (3, 2), (4, 2)}
(ii) {(x, y): x ∈ A, y ∈ B is surname of x} where A is the set of people in India and B is the set of surnames.
(iii) {(x, y) : x ∈ A, ∈ B, y is the area of a square of side x} where A is the set of measurements of length.
(iv) {(x, j): x ∈ B, y ∈ P, y is passenger on x} where B is the set of buses of a school and P is the set of pupils of some schools.
(v) {(x, y) : x ∈ A, y ∈ B, y is sewn onto y}, where A is the set of buttons and B is the set of shirts.
Sol: (i) since each element has unique image.
∴ given relation represents a function.
(ii) Since a unique people can have more than one surname. given relation is not a function.
(iii) Given relation = {(x, y): x ∈ A, y ∈ B, y is the area of square with side x} where A is the set of measurements of length.
Clearly y = x²
So each element has unique image.
Thus given relation represents a function.
(iv) Since a bus contains so many pupils of some schools. So one element have so many images.
Hence each element does not have unique image.
∴ given relation is not a function.
(v) Since if a button sewn on one shirt then it can’t be sewn on other shirt.
Thus each element has unique image.
∴ given relation represents a function.
Que-4: The ordered pairs are represented by the points shown. For each diagram, state whether it represents a relation or a function. Justify your answer.
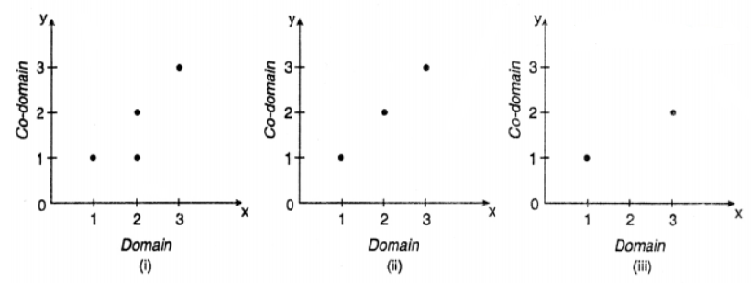
Sol: (i) From graph, it is observe that set of ordered pairs be : {(1, 1), (2, 1), (2, 2), (3, 3)}
Clearly it is a subset of A x B and hence represents a relation. But element 2 has two images 1 and 2.
∴ given relation does not represents a function.
As each element does not have unique image.
(ii) From graph, set of ordered pairs be {(1, 1), (2, 2), (3, 3)}
Since no two ordered pairs have the same first component i.e. each element has unique image.
∴ given set represents a function.
(iii) From graph, the set of ordered pair be {(1, 1), (3, 2)} clearly it is a subset of AxB and hence represents a relation
Here the element 2 in domain does not have any image in codomain.
∴ it neither represents a function.
Que-5: The range and domain of a function f(x) = (3/x) + 1 are subsets of A and B respectively, where A = {(-1/2), 0, (2/3), (6/7), 1} and B = {- 5, 0, {4*(1/2)}, 5, 5, (1/2)}. List the elements of the function as ordered pairs.
Sol:
Que-6: Which of the four statements given below is different from other?
(a) f : A → B
(b) f : x → f(x)
(c) f is a mapping of A and B
(f) f is a function of A into B
Sol: In option (a)fis a function from A into B
So option (c) and (d) ares also coincide with option (a).
f : x → f(x) is also defined as function from A to B
Thus all the four statements are same.
Que-7: A = {- 2, – 1, 1, 2} and f = {x, (1/x), x ∈ A}
(i) List the domain of f
(ii) List the range of f
(iii) Is f a function ?
Sol: Given f be a function defined by f(x) = (1/x) ∀ x ∈ A where A = {- 2, – 1, 1, 2}
f(-2) = -1/2; f(-1) = -1 ∈ A
f(1) = 1 ∈ A; f(2) = 1/2
Thus f = {(-1,-1), (1,1), (-2,(-1/2)), (2,(1/2))}
Domain (f) = {-1, 1, -2, 2}
Range (f) = {-1, 1, (-1/2), (1/2)}
Since each element in domain of f has unique image, i.e. no two ordered pairs have same first component.
∴ f represents a function.
Que-8: f : x → highest prime factor of x.
(i) Find the range of f when the domain is {12, 13, 14, 15, 16 and 17}
(ii) State a domain of five integers for which the range is (3).
(iii) A set of positive integers is called S. What can be said about these integers if (S) = S ?
Sol: Given f : x → highest prime factor of x
(i) Here factors of 12 are 1, 2, 3, 4, 6, 12
∴ 3 be the highest prime factor of 12.
∴ 3 ∈ Rf
factors of 13 are 1 and 13
∴ 13 be the highest prime factor of 13
∴ 13 ∈ Rf
Since 1, 2, 7, 14 are the factors of 14
∴ 7 be the highest prime factor of 14.
∴ 7 ∈ Rf
Since 1, 3, 5, 15 are the factors of 15.
Here 5 be the highest prime factor of 15
∴ 5 ∈ Rf
Since 1, 2, 4, 8 and 16 are the factors of 16
Here 2 be the highest prime factors of 16
∴ 2 ∈ Rf
Since 1, 17 are factors of 17. Here 17 be the highest prime factor of 17. ∴ 17 ∈ Rf
∴ range (f) = {2, 3. 5, 7, 13, 17}
(ii) given Rf = 3 i.e. highest prime factor of each element of domain of f be 3.
Since 3 be the highest prime factor of 3, 6, 9, 12, 18. [since highest prime factor of 15 be 5]
∴ Required Df = {3, 6, 9, 12, 18}
(iii) Given f(S) = S
i. e. highest prime factors of S is equal to S which is only possible if S be the set of all prime numbers. Since factors of any prime number p are 1 and p.
So p be the highest prime factor of p.
Que-9: What is the fundamental difference between a function and a relation? Let X = {1,2, 3, 4} and Y = {1, 5, 9, 11, 15, 16}. Determine which of the following sets are :
(i) relation
(ii) function
(iii) neither
(a) f1 = {(x, y) : y = x², x ∈ X, y ∈ Y}
(b) f2 = {(1, 1), (2, 11), (3, 1), (4, 15)}
(c) f3 = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}
(d) f4 = {(1, 1), (2, 7), (3, 5)}
Sol: If X and Y are non empty sets.
Then any subset of X × Y be a relation from X to Y. Further a function is a special type of relation in which no two ordered pairs have same first component.
(a) Given X = {1, 2, 3, 4} and Y = {1, 5, 9, 11, 15, 16}
Also, given f1 = {(x, y) : y = x², x ∈ X, y ∈ Y}
When x = 1 ∈ X ⇒ y = 1² = 1 ∈ Y ⇒ (1, 1) ∈ f1
When x = 2 ∈ X ⇒ y = 2² = 4 ∈ Y ⇒ (2, 4) ∉ f1
When x = 3 ∈ X ⇒ y = 3² = 9 ∉ Y ⇒ (3, 9) ∈ f1
When x = 4 ∈ X ⇒ y = 4² = 16 ∈ Y ⇒ (4, 16) ∈ f1
∴ f1 = {(1, 1), (3, 9), (4, 16)} clearly each ordered pair is a member of X × Y
∴ f1 represents a relation from X to Y.
Further an element 2 in X has no image in Y.
∴ f1 does not represents a function.
(b) Given f2 = {(1, 1), (2, 11), (3, 1), (4, 15)}
Clearly each ordered pair of f2 is a member of X x Y. Also no two ordered pairs have same first component.
∴ f2 represents a function.
(c) Given f3 = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}
Clearly each ordered pair of f3 be a member of X x Y.
∴ f3 ⊆ X x Y
∴ f3 represents a relation from X to Y. Further element 2 in X have two images 9 and 11 in Y.
∴ f3 does not represents a function.
(d) Given f4 = {(1, 1), (2, 7), (3,5)}
Further (2, 7), ∉ X x Y
∵ f4 is neither a relation nor a function.
Que-10: A certain jet plane has an average speed of 500 km per hour. It can carry sufficient fuel for a 5 hour flight.
(i) Define the relation, as a set, between the distance d (in km) and time t (in hours) for this plane.
(ii) State the domain of the relation.
(iii) State the range of this relation.
(iv) Is this relation a function ?
Sol: (i) Since speed = distance/time
500 = d/t
d = 500t
∴ required relation R = {(t, d) : d = 500t, t ∈ R and t ≤ 5}
(ii) Domain (R) = {t: 0 < t ≤ 5, t ∈ R}
(iii) Range (R) = {d : 0 < d ≤ 2500, d ∈ R} [∵ 0 < t ≤ 5 0 < 500t ≤ 2500 ⇒ 0 < d ≤ 2500]
(iv) Clearly each element in domain of R has unique image i.e. no two ordered pairs have same first component.
∴ given relation represents a function.
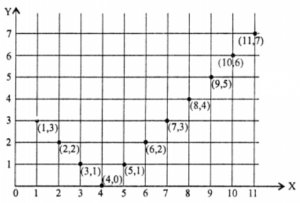
Que-11: The domain of a function is the set of positive integers less than 12. If y find all ordered pairs satisfying the function. Graph the function.
Sol: Clearly Df = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}
Given y = f(x) = | X -4|
When x = 1 ⇒ y = | 1 – 4 | = 3 ⇒ (1, 3) ∈ f
When x = 2 ⇒ y = | 2 – 4 | = 2 ⇒ (2, 2) ∈ f
When x = 3 ⇒ y = | 3 – 4 | = 1 ⇒ (3, 1) ∈ f
When x = 4 ⇒ y = | 4 – 4 | = 0 ⇒ (4, 0) ∈ f
When x = 5 ⇒ y = | 5 – 4 | = 1 ⇒ (5, 1) ∈ f
When x = 6 ⇒ y = | 6 – 4 | = 2 ⇒ (6, 2) ∈ f
When x = 7 ⇒ y = | 7 – 4 | = 3 ⇒ (7, 3) ∈ f
When x = 8 ⇒ y = | 8 – 4 | = 4 ⇒ (8, 4) ∈ f
When x = 9 ⇒ y = | 9 – 4 | = 5 ⇒ (9, 5) ∈ f
When x= 10 ⇒ y = | 10 – 4 | = 6 ⇒ (10, 6) ∈ f
When x = 11 ⇒ y = |11 – 4 | = = 7 ⇒ (11, 7) ∈ f
∴ f = {(1, 3), (2, 2), (3, 1), (4, 0), (5, 1), (6, 2), (7, 3), (8, 4), (9, 5), (10, 6), (11, 7)
Que-12: Let X = {2, 3} and Y = {1, 3, 5}. How many different functions are there from X into Y ?
Sol: We know that if f: A → B be a function s.t n (A) = m and n (B) = n
Then no. of functions from A to B = [n (B)]n(A) = nm
Here X = {2, 3} ∴ n (X) = 2 and Y = {1, 3, 5} ∴ n (Y) = 3
Thus, required no. of functions from X into Y = [n (Y)]^{n(x)} = 3² = 9
–: End Relation and Functions Class 11 OP Malhotra Exe-2C ISC Math Ch-2 Solutions :–
Return to :- OP Malhotra ISC Class-11 S Chand Publication Maths Solutions
Thanks
Please share with your friends


