Section And Mid Point Formula Concise Maths Solutions

Section And Mid Point Formula Concise Maths Solutions Chapter-13.Solutions of Exercise – 13 (A), Exercise – 13 (B),Exercise – 13 (C), Exercise – 13 (D) for Concise Selina Maths of ICSE Board Class 10th. Concise Solutions Section And Mid Point Formula Chapter – 13 for ICSE Maths Class 10 is available here. All Solutions of Concise Selina of Chapter-13 Section And Mid Point Formula has been solved according instruction given by council. This is the  Solutions of Chapter-13 Section And Mid Point Formula for ICSE Class 10th. ICSE Maths text book of Concise is In series of famous ICSE writer in maths publications. Concise is most famous among students.

Section And Mid Point Formula Concise Maths Solutions Chapter-13

The Solutions of Concise Mathematics Chapter 12 Reflection for ICSE Class 10 have been solved.  Experience teachers Solved Chapter-12 Reflection to help students of class 10th ICSE board. Therefore the ICSE Class 10th Maths Solutions of Concise Selina Publishers helpful on  various topics which are prescribed in most ICSE Maths textbook

–:Select Topic :–

 Exercise- 12(A) ,     Exercise- 12(B) ,      Exercise – 13 (C),   

How to Solve Concise Maths Selina Publications Chapter-13 Section And Mid Point Formula

Note:- Before viewing Solutions of Chapter -13 Section And Mid Point Formula of Concise Selina Maths read the Chapter-13 Carefully then solve all example of your text book. The Chapter- 13 Section And Mid Point Formula is main Chapter in ICSE board

 

EXERCISE – 13( A) Solutions of Concise Maths Section And Mid Point Formula

 

Question 1.

Calculate the co-ordinates-of the point P which divides the line segment joining:
(i) A (1, 3) and B (5, 9) in the ratio 1 : 2
(ii) A (-4, 6) and B (3, -5) in the ratio 3 : 2

Answer 1

(i) Let co-ordinates of P be (x,y)

Question 2.

Answer 2

Let the point P (x, 0) divides in the ratio of m₁ : m₂ line joining the points A (2, -3) and B (5, 6)

Question 3.

In what ratio is the line joining (2, -4) and (-3, 6) divided by the y-axis ?

Answer 3

Let the point P (0, y) divides the line joining the points A (2, -4) and (-3, 6) in the ratio of m₁ : m₂

Question 4.

Answer 4

Let the point P (1, a) divides the line joining the points (-1, 4) and (4, -1) in the ratio of m₁ : m₂

Question 5.

In what ratio does the point (a, 6) divide the join of (-4, 3) and (2, 8) ? Also, find the value of ‘a’.

Answer 5

Let the point P (a, 6) divides the line joining the points A (-4, 3), B (2, 8) in the ratio of m₁ : m₂

Question 6.

In what ratio is the join of (4, 3) and (2, -6) divided by the x-axis. Also, find the co-ordinates of the point of intersection.

Answer 6

Find the ratio in which the join of (-4, 7) and (3, 0) is divided by the y-axis. Also, find the co-ordinates of the point of intersection.

Answer 7

Let, the points (0, y) be the point of intersection which divides the line joining the points A (-4, 7) and B (3, 0)

Question 8.

Points A, B, C and D divide the line segment joining the point (5, -10) and the origin in five equal parts. Find the co-ordinates of A, B, C and D.

Answer 8

Points A, B, C and D divide the line segment joining the points (5, -10) and origin (0, 0) in five equal parts
Let co-ordinates of A be (x, y) which divides PO in the ratio of 1 : 4

Question 9.

Answer 9 

Let the co-ordinates of P be (x, y) which divides the line joining the points A (-3,-10) and B (-2,6) in the ratio of AP : PB i.e. (5 – 1) : 1 or 4 : 1

Question 10.

P is a point on the line joining A (4, 3) and B (-2, 6) such that 5AP = 2BP. Find the co-ordinates of P.

Answer 10

Question 11.

Calculate the ratio in which the line joining the points (-3, -1) and (5, 7) is divided by the line x = 2. Also, find the co-ordinates of the point of intersection.

Answer 11

Let the point P (2, y) divides the line joining the points A (-3, -1) and B (5, 7) in the ratio of m₁ : m₂

Question 12.

Calculate the ratio in which the line joining A (6, 5) and B (4, -3) is divided by the line y = 2.

Answer 12

Let the point P (x, 2) divides the line joining the points A (6, 5) and B (4, -3) in the ratio of m₁ : m₂

Question 13.

The point P(5, -4) divides the line segment AB, as shown in the figure, in the ratio 2 : 5. Find the co-ordinates of points A and B.

Answer 13

From the figure, the line AB intersects x-axis at A and y-axis at B.
Let the co-ordinates of A (x, 0) and B (0, y) and P (5, -4) divides it in the ratio of 2 : 5

Question 14.

Find the co-ordinates of the points of trisection of the line joining the points (-3, 0) and (6, 6).

Answer 14

Question 15.

Show that the line segment joining the points (-5, 8) and (10, -4) is trisected by the co-ordinate axes.

Answer 15

Let the points A (-5, 8) and B (10, -4).
Let P and Q be the two points on the axis which trisect the line joining the points A and B.
AP = PQ = QB
AP : PB = 1 : 2 and AQ : QB = 2 : 1

Question 16.

Show that A (3, -2) is a point of trisection of the line-segment joining the points (2, 1) and (5, -8). Also, find the co-ordinates of the other point of trisection.

Answer 16

Let A and B are the points of trisection of the line segment joining the points P (2, 1) and Q (5, -8), then
PA = AB = BQ.
PA : AQ = 1 : 2 and PB : BQ = 2 : 1

Question 17.

If A = (-4, 3) and B = (8, -6)
(i) find the length of AB
(ii) In what ratio is the line joining A and B, divided by the x-axis ?

Answer 17

Question 18.

The line segment joining the points M (5, 7) and N (-3, 2) is intersected by the y-axis at point L. Write down the abscissa of L. Hence, find the ratio in which L divides MN. Also, find the co-ordinates of L.

Answer 18

Question 19.

A (2, 5), B (-1, 2) and C (5, 8) are the co-ordinates of the vertices of the triangle ABC. Points P and Q lie on AB and AC respectively, such that:
AP : PB = AQ : QC = 1 : 2.
(i) Calculate the co-ordinates of P and Q.
(ii) Show that PQ =  BC.

Answer 19

Question 20.

A (-3, 4), B ( 3, -1) and C (-2, 4) are the vertices of a triangle ABC. Find the length of line segment AP, where point P lies inside BC, such that BP: PC = 2 : 3.

Answer 20

Question 21.

The line segment joining A (2, 3)and B(6, -5) is intercepted by x-axis at the point K. Write down the ordinate of the point K. Hence, find the ratio in which K divides AB. Also, find the co-ordinates of the point K. [1990, 2006]

Answer 21 

Let the line segment Intersect the x-axis at the point P
Co-ordinates of P are (x, 0)
Let P divide the line segment in the ratio K : 1 then

Question 22.

The line segment joining A (4, 7) and B (-6, -2) is intercepted by the y-axis at the point K. Write down the abscissa of the point K. Hence, find the ratio in which K divides AB. Also, find the co-ordinates of the point K.
Solution:

Answer 22

Points A (4, -7), B (-6, -2) are joined which intersects y-axis at K. abscissa of K will be 0

Let the coordinates of K be (0, y) and K divides AB line segment in the ratio m₁ : m₂

Question 23.

The line joining P (-4, 5) and Q (3, 2), intersects they axis at point R. PM and QN are perpendiculars from P and Q on the x-axis. Find:
(i) The ratio PR: RQ.
(ii) The co-ordinates of R.
(iii) The areas of the quadrilateral PMNQ. [2004]

Answer 23

(i) Let divides the line joining the points P (-4, 5) and Q (3, 2) in the ratio k : 1

Question 24.

In the given figure, line APB meets the x- axis at point A and y-axis at point B. P is the point (-4, 2) and AP : PB = 1 : 2. Find the co-ordinates of A and B.

Answer 24

Let the co-ordinates of A be (x1, 0) (as it lies on x-axis)
and co-ordinates of B be (0, y2)
and co-ordinates of P are (-4, 2)
AP : PB = 1 : 2 i.e. m1 = 1, m2 = 2
Now, P divides AB in the ratio m₁ : m₂ or 1 : 2

Question 25.

Given a line segment AB joining the points A (-4, 6) and B (8, -3). Find:
(i) the ratio in which AB is divided by the y-axis.
(ii) find the coordinates of the point of intersection.
(iii) the length of AB.

Answer 25

(i) Let the y-axis divide AB in the ratio m : 1

Question 26

If P(-b, 9a – 2) divides the line segment joining the points A(-3, 3a + 1) and B(5, 8a) in the ratio 3: 1, find the values of a and b.

Answer 26

Take (x₁ , y₁) = (-3, 3a + 1) ; (x₂ , y₂) = B(5, 8a) and

(x, y) = (-b, 9a – 2)

Here m₁ = 3 and m₂ =1

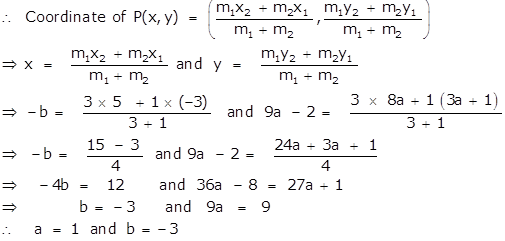
Solutions of Selina Publishers Concise Maths Section And Mid Point Formula, EXERCISE- 13 B

 

Question 1.

Find the mid-point of the line segment joining the points:
(i) (-6, 7) and (3, 5)
(ii) (5, -3), (-1, 7)

Answer 1

Let P (x, y) be the mid-point in each case

Question 2

Points A and B have co-ordinates (3, 5) and (x, y) respectively. The mid-point of AB is (2, 3). Find the values of x and y.

Answer 2

Co-ordinates of A (3, 5), B (x, y) and mid-point M (2, 3)

Question 3

A (5, 3), B (-1, 1) and C (7, -3) are the vertices of ABC. If L is the mid-point of AB and M is the mid-point of AC, show that LM =  BC.

Answer 3

Given M is the mid-point of AB, find the co-ordinates of:
(i) A; if M = (1, 7) and B = (-5, 10),
(ii) B; if A = (3, -1) and M (-1, 3).

Answer 4

M is the mid-point of AB.
(i) Let A = (x, y), M = (1, 7) and B = (-5, 10)

P (-3, 2) is the mid-point of line segment AB as shown in the figure. Find the co-ordinates of points A and B.

Answer 5

Point A is on y-axis
its abscissa is zero and point B is on x-axis
its ordinate is zero.
Now, let co-ordinates of A are (0, y) and ofB are (x, 0) and P (-3, 2) is the mid-point

Answer 6

Points A and B are on x-axis and y-axis respectively
Ordinate of A is zero and abscissa of B is zero.
Let co-ordinates of A be (x, 0) and B (0, y)
and P (4, 2) is the mid-point

Question 7

(-5, 2), (3, -6) and (7, 4) arc the vertices of a triangle. Find the length of its median through the vertex (3, -6) and (7, 4).

Answer 7

Let A (-5, 2), B (3, -6) and C (7, 4) are the vertices of a ABC
Let L,M and N are the mid-points of sides BC, CA and AB respectively of ABC.
L is the mid-point of BC.
Co-ordinates of L will be

Given a line ABCD in which AB = BC = CD, B = (0, 3) and C = (1, 8). Find the co-ordinates of A and D.

Answer 8

Question 9

One end of the diameter of a circle is (-2, 5). Find the co-ordinates of the other end of it, if the centre of the circle is (2, -1).

Answer 9

Question 10

A (2, 5), B (1, 0), C (-4, 3) and D (-3, 8) are the vertices of quadrilateral ABCD. Find the co-ordinates of the mid-points of AC and BD. Give a special name to the quadrilateral.

Answer 10

Co-ordinates of A = (2, 5), B = (1, 0), C = (-4, 3) and D = ( 3, 8)

Let the mid-point of AC is P (x1, y1) Co-ordinates of mid-point of AC will be

Co-ordinates of mid-points AC and BD are the same..
The quadrilateral is a parallelogram.

Question 11

P (4, 2) and Q (-1, 5) are the vertices of parallelogram PQRS and (-3, 2) are the co-ordinates of the point of intersection of its diagonals. Find the co-ordinates of R and S.

Answer 11

In the parallelogram PQRS and qo-ordinates of P are (4, 2) and of Q are (-1, 5).
The diagonals of || gm AC and BD intersect each other at O (-3, 2)

Question 12

A (-1, 0), B (1, 3) and D (3, 5) are the vertices of a parallelogram ABCD. Find the co-ordinates of vertex C.

Answer 12

Vertices of a parallelogram ABCD are A (-1, 0), B (1, 3) and D(3, 5)
Let co-ordinates of C be (x, y)
Let the diagonals AC and BD bisect each other at O. Then O is the mid-point of AC as well as of BD.
Co-ordinates of O, the mid-point of BD will be

Question 13

The points (2, -1), (-1, 4) and (-2, 2) are the mid-points of the sides of a triangle. Find its vertices.

Answer 13

Let D, E and F are the mid-points of sides BC, CA and AB of a ABC respectively.


Co-ordinates of A are (-5, 7), of B are (1, -3) and of C are (3, 1)

Question 14

Points A (-5, x), B (y, 7) and C (1, -3) are collinear (i.e. lie on the same straight line) such that AB = BC. Calculate the values of x and y.

Answer 14

Question 15

Points P (a, -4), Q (-2, b) and R (0, 2) are collinear. If Q lies between P and R, such that PR = 2QR, calculate the values of ‘a’ and ‘b’:

Answer 15

 

Question 16

Calculate the co-ordinates of the centroid of the triangle ABC, if A = (7, -2), B = (0, 1) and C = (-1, 4).

Answer 16

Question 17

The co-ordinates of the centroid of a triangle PQR are (2, -5). If Q = (-6, 5) and R = (11, 8); calculate the co-ordinates of vertex P.

Answer 17

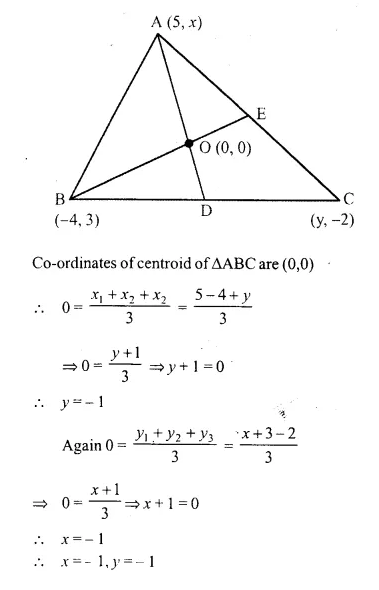
Question 18

.A (5, x), B (-4, 3) and C (y, -2) are the vertices of the triangle ABC whose centroid is the origin. Calculate the values of x and y.

Answer 18

 

 EXERCISE – 13 (C) Section And Mid Point Formula Concise Maths Solutions Selina Publishers

 

Question 1

Given a triangle ABC in which A = (4, -4), B (0, 5) and C = (5, 10). A point P lies on BC such that BP : PC = 3 : 2. Find the length of line segment AP.

Answer  1

B (0, 5), C (5, 10) and BP : PC = 3 : 2 Co-ordinates of P will be

A (20, 0) and B (10, – 20) are two fixed points, find the co-ordinates of the point P in AB such that 3PB = AB. Also, find the co-ordinates of some other point Q in AB such that AB = 6AQ.

Answer 2

(i) A (20, 0), B (10, – 20)

Question 3

A (-8, 0), B (0, 16) and C (0, 0) are the vertices of a triangle ABC. Point P lies on AB and Q lies on AC such that AP : PB = 3 : 5 and AQ : QC = 3 : 5. Show that: PQ =  BC.

Answer 3

Question 4

Find the co-ordinates of points of trisection of the line segment joining the points (6, -9) and the origin.

Answer 4

Points are A (6, -9) and O (0,0) let P and Q are points, which trisect AO

A line segment joining A (-1, ) and B (a, 5) is divided in the ratio 1 : 3 at P, the point where the line segment AB intersects the y-axis.
(i) Calculate the value of ‘a’.
(ii) Calculate the co-ordinates of ‘P’. (1994)

Answer 5

In what ratio is the line joining A (0, 3) and B (4, -1), divided by the x-axis ? Write the co-ordinates of the point where AB intersects the x-axis. [1993]

Answer 6

Let the ratio be m₁ : m₂ when the x-axis intersects the line AB at P.

Question 7

The mid point of the segment AB, as shown in diagram, is C (4, -3). Write down the co-ordinates of A and B. (1996)

Answer  7

Let co-ordinates of A (x, 0) and B (0, y) and C (4, -3) the mid point of AB.

Question 8

AB is a diameter of a circle with centre C = (-2, 5). If A = (3, -7). Find
(i) the length of radius AC
(ii) the coordinates of B.

Answer  8

Question 9

Find the co-ordinates of the centroid of a triangle ABC whose vertices are A (- 1, 3), B (1, – 1) and C (5, 1)

Answer  9

Question 10

The mid-point of the line segment joining (4a, 2b – 3) and (-4, 3b) is (2, -2a). Find the values of a and b.

Answer  10

Let A and B are two points and P is its mid point then A is (4a, 2b -3), B(-4, 2b) and P is (2, -2a)

Question 11

The mid point of the line segment joining (2a, 4) and (-2, 2b) is (1, 2a + 1). Find the value of a and b.

Answer  11

The midpoint of the line segment joining (2a, 4) and (-2, 2b) is (1, 2a + 1)

Question 12

(i) Write down the co-ordinates of the point P that divides the line joining A (-4, 1) and B (17, 10) in the ratio 1 : 2.
(ii) Calculate the distance OP, where O is the origin.
(iii) In what ratio does the y-axis divide the line AB ? [ICSE 1995]

Answer  12

Point P, divides a line segment giving the points A (-4, 1) and B (17, 10) is the ratio 1 : 2.

Question 13

Prove that the points A(-5, 4); B (-1, -2) and C (5, 2) are the vertices of an isosceles right-angled triangle. Find the co-ordinates of D. So that ABCD is a square. [1992]

Answer  13

In ABC, the co-ordinates of A, B and C are (-5, 4), B(-1, -2) and C (5, 2) respectively.

ABC is also a right-angled triangle.
Hence ABC is an isosceles right angled triangle,
Let D be the fourth vertex of square ABCD and co-ordinates of D be (x,y)
Since the diagonals of a square bisect each other and let O be the point of intersection of AC and BD.
O is mid-point of AC as well as BD.

Question 14

M is the mid-point of the line segment joining the points A (-3, 7) and B (9, -1). Find the co-ordinates of point M. Further, if R (2, 2) divides the line segment joining M and the origin in the ratio p : q, find the ratio p : q.

Answer 14

Two points are given A (-3, 7) and B (9, -1)
M is the mid-point of line joining AB.
Co-ordinates of M wll be

Question 15

Calculate the ratio in which the line joining A (-4, 2) and B (3, 6) is divided by point P (x, 3). Also find
(i) x
(ii) Length of AP. (2014)

Answer  15

Let ratio = k : 1

Question 16

Find the ratio in which the line 2x + y = 4 divides the line segment joining the points P (2, -2) and Q (3, 7).

Answer 16

Let the given line 2x + y = 4 divides the line segment joining the points P (2, -2) and Q (3,7) in the ratio k : 1 at a point (x, y) on it.

Question 17

If the abscissa of a point P is 2. Find the ratio in which this point divides the line segment joining the points (-4, 3) and (6, 3). Also, find the co-ordinate of point P.

Answer 17

Abscissa of a point P is 2
Let co-ordinates of point P be (2, y)
Let point P (2, y) divides the line segment joining the points (-4, 3) and (6, 3) in the ratio k : 1

Question 18

The line joining the points (2, 1) and (5, -8) is trisected at the points P and Q. If point P lies on the line 2x – y + k = 0, find the value of k, Also, find the co-ordinates of point Q.

Answer  18

A line joining the points (2, 1) and (5, -8) is trisector at P and Q.

Question 19

M is the mid-point of the line segment joining the points A (0, 4) and B (6, 0). M also divides the line segment OP in the ratio 1 : 3. Find:
(i) co-ordinates of M
(ii) co-ordinates of P
(iii) length of BP

Answer 19

M is mid point of the line segment joining the points A (0, 4) and B (6, 0)
M divides the line segment OP in the ratio 1 : 3

Question 20

Find the image of the point A (5, -3) under reflection in the point P (-1, 3).

Answer 20

Image of the point A (5, -3) under reflection in the point P (-1, 3)
Let B (x, y) be the point of reflection of A (5, -3) under P(-1, 3)

Question 21

A (-4, 2), B (0, 2) and C (-2, -4) are vertices of a triangle ABC. P, Q and R are mid-points of sides BC, CA and AB respectively. Show that the centroid of PQR is the same as the centroid of ABC.

Answer 21

A (-4, 2), B (0, 2) and C (-2, -4) are the vertices of ABC.
P, Q and R are the mid-points of the sides BC, CA and AB respectively.
G is the centroid of medians AP, BQ and CR.
Co-ordinates of G are