ML Aggarwal Section Formula Exe-11 Solutions ICSE Class-10 Maths Ch-11

ML Aggarwal Section Formula Exe-11 Solutions ICSE Class-10 Maths Ch-11. We Provide Step by Step Answer of Exercise-11 Section Formula Exe-11 Questions for ICSE Class-10 APC Understanding Mathematics. Visit official Website CISCE for detail information about ICSE Board Class-10.

ML Aggarwal Section Formula Exe-11 Solutions ICSE Class-10 Maths Ch-11

Board	ICSE
Subject	Maths
Class	10th
Chapter-11	Section Formula
Writer / Book	Understanding
Topics	Solutions of Exe-11
Academic Session	2024-2025

ML Aggarwal Section Formula Exe-11 Solutions

ICSE Class-10 Maths Ch-11

Question -1. Find the co-ordinates of the mid-point of the line segments joining the following pairs of points:

(i) (2, – 3), ( – 6, 7)
(ii) (5, – 11), (4, 3)
(iii) (a + 3, 5b), (2a – 1, 3b + 4)

Answer:

(i) Co-ordinates of the mid-point of (2, -3), ( -6, 7)

{(x₂ + x₂)/2, (y₁ + y₂)/2} or

{(2 – 6)/2, (-3 + 7)/2} or

(-4/2, 4/2) or (-2, 2)

(ii) Mid-point of (5, – 11) and (4, 3)

= {(x₁ + x₂)/2, (y₁ + y₂)/2} or

{(5+4)/2, (-11+3)/2}

Or (9/2, -8/2) or (9/2, – 4)

(iii) Mid-point of (a + 3, 5b) and (2a – 1, 3b + 4)

= (x₁ + x₂)/2, (y₁ + y₂)/2

Or (a + 3 + 2a – 1)/2, (5b + 3b + 4)/2

Or (3a + 2)/2 , (8b + 4)/2

Or {(3a + 2)/2, (4b + 2)}

Question -2. P divides the distance between A ( – 2, 1) and B (1, 4) in the ratio of 2 : 1. Calculate the co-ordinates of the point P.

Answer :

Points are A (-2, 1) and B (1, 4) and
Let P (x, y) divides AB in the ratio of m₁ : m₂ i.e. 2 : 1
Co-ordinates of P will be

x = (m₁x₂ + m₂x₁)/(m₁ + m₂)

= {(2×1 + 1×(-2)}/(2+1)

= (2 – 2)/3

= 0/3

= 0

y = (m₁y₂ + m₂y₁)/(m₁ + m₂)

= (2×4 + 1×1)/(2+1)

= (8 + 1)/3

= 9/3

= 3

∴ Co-ordinates of point P are (0, 3).

Question -3. 

(i) Find the co-ordinates of the points of trisection of the line segment joining the point (3, – 3) and (6, 9).
(ii) The line segment joining the points (3, – 4) and (1, 2) is trisected at the points P and Q. If the coordinates of P and Q are (p, – 2) and  respectively, find the values of p and q.

Answer :

(i) Let P (x₁, y₁) and Q (x₂, y₂) be the points which trisect the line segment joining the points A (3, -3) and B (6, 9)

∵ P(x₁, y₁) divides AB in the ratio of 1 : 2

∴ x₁ = (m₁x₂ + m₂x₁)/(m₁ + m₂)

= (1×6 + 2×3)/(1+2)

= (6 + 6)/3

= 12/3

= 4

y₁ = (m₁y₂ + m₂y₁)/(m₁ + m₂)

= {(1×9 + 2×(-3)}/(1+2)

= (9 – 6)/3

= 3/3

= 1

∴ Co-ordinates of Pare (4, 1)

∵ Q (x₂, y₂) divides the line segment

AB in the ratio of 2 : 1

∴ x₂ = (m₁x₂ + m₂x₁)/(m₁ + m₂)

= (2×6 + 1×3)/(2+1)

= (12 + 3)/3

= 15/3

= 5

y₂ = (m₁y₂ + m₂y₁)/(m₁ + m₂)

= {2×9 + 1(-3)}/(2+1)

= (18 – 3)/3

= 15/3

= 5

∴ Co-ordinates of Q are (5, 5)

(ii) point P and Q trisect the line AB.

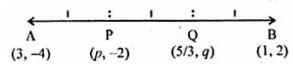
In other words, P divides it in the ratio 1 : 2 and Q divides it in the ratio 2 : 1

∴ p = (mx₂ + nx₁)/(m + n)

= (1×1 + 2×3)/(1+2)

= (1 + 6)/3

= 7/3

q = (my₂ + ny₁)/(m + n)

= {2×2 + 1×(-4)}/(2+1)

= (4 – 4)/2

= 0

∴ p = 7/3, q = 0

Question -4. The line segment joining the points A (3, 2) and B (5, 1) is divided at the point P in the ratio 1 : 2 and it lies on the line 3x – 18y + k = 0. Find the value of k.

Answer :

The point P (x, y) divides the line segment joining the points
A (3, 2) and B (5, 1) in the ratio 1 : 2

∴ x = (mx₂ + nx₁)/(m + n)

= (1 × 5 + 2 × 3)/(1+2)

= (5 + 6)/2

= 11/3

y = (my₂ + ny₁)/(m + n)

= (1 × 1 + 2 × 2)/(1+2)

= (1 + 4)/3

= 5/3

∵ P lies on the line 3x – 18y + k = 0

∴ It will satisfy it.

3(11/3) – 18(5/3) + k = 0

⇒ 11 – 30 + k = 0

⇒ – 19 + k = 0

⇒ k = 19

Question -5. m Find the coordinates of the point which is three-fourth of the way from A (3, 1) to B ( – 2, 5).

Answer:

Let P be the required point, then
AP/AB = 3/4

∴ AP/AB = 3/4

= AP/(AP + PB) = 3/4

⇒ 4AP = 3AP + 3PB

⇒ 4AP – 3AP = 3PB

AP = 3PB

AP/PB = 3/1

∴ m₁ = 3, m₂ = 1

Let co-ordinates of P be (x, y)

∴ x = (m₁x₂ + m₂x₁)/(m₁ + m₂)

= {3 × (-2) + 1 × (3)}/(3 + 1)

= (-6 + 3)/ 4

= -3/4

y = (m₁y₂ + m₂y₁)/(m₁ + m₂)

= (3 × 5 + 1 × 1)/(3 + 1)

= (15 + 1)/4

= 16/4

= 4

∴ Co-ordinates of P will be (-3/4, 4)

Question -6. The line segment joining A ( – 3, 1) and B (5, – 4) is a diameter of a circle whose centre is C. find the co-ordinates of the point C. 

Answer:

∵ C is the centre of the circle and AB is the diameter
C is the midpoint of AB.
Let co-ordinates of C (x, y)

∴ x = (-3 + 5)/2, x = (1 – 4)/2

⇒ x = 2/2, y = -3/2

⇒ x = 1, y = -3/2

∴ Co-ordinates of C are (1, -3/2)

Question -7. The mid-point of the line segment joining the points (3m, 6) and ( – 4, 3n) is (1, 2m – 1). Find the values of m and n.

Answer :

Let the mid-point of the line segment joining two points
A(3m, 6) and (-4, 3n) is P( 1, 2m – 1)

∴ 1 = (x₁ + x₂)/2

= (3m – 4)/2

⇒ 3m – 4 = 2

⇒ 3m = 2 + 4 = 6

⇒ m = 6/3 = 2

And 2m – 1 = (6 + 3n)/2

⇒ 4m – 2 = 6 + 3n

⇒ 4 × 2 – 2 = 6 + 3n = 8 – 2 = 6 + 3n

⇒ 3n = 8 – 2 – 6 = 0

⇒ n = 0

Hence,

m = 2, n = 0

Question-8. The co-ordinates of the mid-point of the line segment PQ are (1, – 2). The co-ordinates of P are ( – 3, 2). Find the co-ordinates of Q.

Answer :

Let the co-ordinates of Q be (x, y)
co-ordinates of P are (-3, 2) and mid-point of PQ are (1, -2) then

1 = (-3 + x)/2

⇒ – 3 + x = 2

⇒ x = 2 + 3 = 5

And -2 = (2 + y)/2

⇒ 2 + y = -4

⇒ y = – 4 – 2 = – 6

∴ x = 5, y = – 6

Hence, co-ordinates of Q are (5, -6)

Question -9. AB is a diameter of a circle with centre C ( – 2, 5). If point A is (3, – 7). Find:

(i) the length of radius AC.
(ii) the coordinates of B. (2013)

Answer :

Let co-ordinate of B are (x, y)

∴ (3 + x)/2 = -2 and (y – 7)/2 = 5

⇒ 3 + x = – 4 and y – 7 = 10

⇒ x = – 4 – 3 and y = 10 + 7

⇒ x = – 7 and y = 17

∴ B is (-7, 17)

Question -10. Find the reflection (image) of the point (5, – 3) in the point ( – 1, 3).

Answer :

Let the co-ordinates of the images of the point A (5, -3) be

A1 (x, y) in the point (-1, 3) then
the point (-1, 3) will be the midpoint of AA1.

∴ – 1 = (5 + x)/2

⇒ 5 + x = – 2

x = – 2 – 5 = – 7

and 3 = (-3 + y)/2

⇒ – 3 + y = 6

⇒ y = 6 + 3 = 9

∴ Co-ordinates of the image A, will be (-7, 9).

Question -11. The line segment joining A (-1,5/3) the points B (a, 5) is divided in the ratio 1 : 3 at P, the point where the line segment AB intersects y-axis. Calculate

(i) the value of a
(ii) the co-ordinates of P

Answer :

Let P (x, y) divides the line segment joining
the points -1,5/3, B(a, 5) in the ratio 1 : 3

∴ x = {1×a + 3×(-1)}/(1+3)

= (a – 3)/4

y = {1×a + 3×(-1)}/(1+3)

= (a – 3)/4

= (5 + 5)/4

= 10/4

= 5/2

(i) ∵ AB intersects y-axis at P

∴ x = 0

⇒ (a – 3)/4 = 0

⇒ a – 3 = 0

∴ a = 3

(ii) ∴ Co-ordinates of P are (0, 5/2)

Question -12. The point P ( – 4, 1) divides the line segment joining the points A (2, – 2) and B in the ratio of 3 : 5. Find the point B.

Answer :

Let the co-ordinates of B be (x, y)
Co-ordinates of A (2, -2) and point P (-4, 1)
divides AB in the ratio of 3 : 5

∴ -4 = {3×x + 5×(2)}/(3+5)

= (3x +10)/8

And 3x + 10 = – 32

⇒ 3x = – 32 – 10

= – 42

∴ x = – 42/3 = – 14

l = {3×y + 5×(-2)}/(3+5)

⇒ l = (3y – 10)/8

⇒ 3y – 10 = 8

⇒ 3y = 8 + 10

= 18

∴ y = 18/3 = 6

∴ Co-ordinates of B = (- 14, 6)

Question -13.

(i) In what ratio does the point (5, 4) divide the line segment joining the points (2, 1) and (7 ,6) ?
(ii) In what ratio does the point ( – 4, b) divide the line segment joining the points P (2, – 2), Q ( – 14, 6) ? Hence find the value of b.

Answer :

(i) Let the ratio be m₁ : m₂ that the point (5, 4) divides

the line segment joining the points (2, 1), (7, 6).

5 = (m₁×7 + m₂×2)/(m₁ + m₂)

⇒ 5m₁ + 5m₂ = 7m₁ + 2m₂

⇒ 5m₂ – 2m₂ = 7m₁ – 5m₁

⇒ 3m₂ = 2m₁

⇒ m₁/m₂ = 3/2

⇒ m₁ : m₂ = 3 : 2

(ii) The point (- 4, b) divides the line segment joining the points P (2, -2) and Q (-14, 6) in the ratio m₁ : m₂.

∴ -4 = {m₁(-14) + m₂×2}/(m₁+m₂)

⇒ – 4 m₁ – 4m₂ = – 14 m₁ + 2 m₂

⇒ – 4m₁ + 14 m₁ = 2m₂ + 4m₂

⇒ 10m₁ = 6 m₂

⇒ m₁/m₂ = 6/10 = 3/5

⇒ m₁ : m₂ = 3 : 5

Again b = {m₁×6 + m₂×(-2)}/(m₁+m₂)

= (6m₁ – 2m₂)/(m₁+m₂)

⇒ b = (6×3 – 2×5)/(3+5)

= (18 – 10)/8

= 8/8

= 1

b = 1

---

ML Aggarwal Section Formula Exe-11 Solutions

ICSE Class-10 Maths Ch-11

Page-223

Question-14. The line segment joining A (2, 3) and B (6, – 5) is intercepted by the x-axis at the point K. Write the ordinate of the point k. Hence, find the ratio in which K divides AB. Also, find the coordinates of the point K. (2006)

Answer :

Let the co-ordinates of K be (x, 0) as it intersects x-axis.
Let point K divides the line segment joining the points
A (2, 3) and B (6, -5) in the ratio m₁ : m₂.

∴ 0 = (m₁y₂ + m₂y₁)/(m₁+m₂)

⇒ 0 = {m₁×(-5) + m₂×3}/(m₁+m₂)

⇒ -5m₁ + 3m₂ = 0

⇒ -5m₁ = -3m₂

⇒ m₁/m₂ = 3/5

⇒ m₁ : m₂ = 3 : 5

Now,

x = (m₁x₂ + m₂x₁)/(m₁ + m₂)

= (3×6 + 5×2)/(3 + 5)

= (18 + 10)/8

= 28/8

= 7/2

Co-ordinate of K are (7/2, 0)

Question -15. If A ( – 4, 3) and B (8, – 6), 

(i) find the length of AB.
(ii) in what ratio is the line joining AB, divided by the x-axis? (2008)

Answer :

Given A (-4, 3), B (8, -6)

Let O divides AB in the ratio m₁ : m₂

∴ x = (m₁x₂ + m₂x₁)/(m₁+m₂)

⇒ 0 = {m₁×8 + m₂(-4)}/(m₁ + m₂)

⇒ 8m₁ – 4m₂ = 0

⇒ 8m₁ = 4m₂

⇒ m₁/m₂ = 4/8 = 1/2

∴ m₁ : m₂ = 1 : 2

∴ O, divides AB in the ratio 1 : 2

Question -16. In what ratio does the line x – y – 2 = 0 divide the line segment joining the points (3, – 1) and (8, 9)? Also, find the coordinates of the point of division.

Answer :

Let the point A (3, – 1) and point B (8, 9) and let the line x – y – 2 = 0 divide the line segment joining the points A (3, – 1) and B (8, 9) in the ratio m₁ : m₂ at point P (x, y) then

x = (m₁x₂ + m₂x₁)/(m₁+m₂)

= (m₁×8 + m₂×3)/(m₁+m₂)

and y = (m₁y₂ + m₂y₁)/(m₁+m₂)

= {m₁×9 + m₂(-1)}/(m₁+m₂)

= (9m₁ – m₂)/(m₁+m₁)

∵ The point P (x, y) lies on the line x – y – 2 = 0

∴ (8m₁+3m₂)/(m₁+m₂) – (9m₁ – m₂)/(m₁+m₂) – 2 = 0

⇒ 8m₁ + 3m₂ – 9m₁ + m₂ – 2m₁ – 2m₂ = 0

⇒ – 3m₁ + 2m₂ = 0

⇒ 3m₁= 2m₂

⇒ m₁/m₂ = 2/3

∴ Co-ordinates of point P are (5, 3)

Question -17. Given a line segment AB joining the points A ( – 4, 6) and B (8, – 3). Find:

(i) the ratio in which AB is divided by the y-axis.
(ii) find the coordinates of the point of intersection.
(iii)the length of AB. (2012)

Answer :

(i) Let the y-axis divide AB in the ratio m : 1.

therefore

0 = (m×8 – 4×1)/(m+1)

⇒ 8m – 4 = 0

⇒ m = 4/8

⇒ m = 1/2

So, required ratio = 1/2 : 1 or 1 : 2

(ii) Also, y = {1×(-3) + 2×6}/(1+2)

= 9/3

= 3

So, coordinates of the point of intersection are (0, 3)

(iii)

 

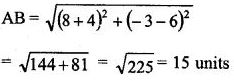
Question -18. Calculate the length of the median through the vertex A of the triangle ABC with vertices A (7, – 3), B (5, 3) and C (3, – 1)

Answer :

Let D (x, y) be the median of ΔABC through A to BC.
∴ D will be the midpoint of BC
∴ Co-ordinates of D will be,

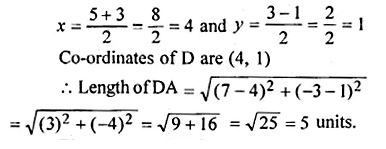
Question-19. Three consecutive vertices of a parallelogram ABCD are A (1, 2), B (1, 0) and C (4, 0). Find the fourth vertex D.

Answer :

Let O in the mid-point of AC the diagonal of ABCD
∴ Co-ordinates of O will be

{(1 + 4)/2, (2 + 0)/2} or (5/2, 1)

∵ OA also find the mid point of second diagonal BD and let co-ordinates of D be (x, y)

∴ 5/2 = (1 + x)/2

⇒ 10 = 2 + 2x

⇒ 2x = 10 – 2 = 8

∴ x = 8/2 = 4

And l = (0 + y)/2

⇒ y = 2

∴ Co-ordinates of D are (4, 2)

Question- 20. If the points A ( – 2, – 1), B (1, 0), C (p, 3) and D (1, q) from a parallelogram ABCD, find the values of p and q.

Answer :

A (-2, -1), B (1, 0), C (p, 3) and D (1, q)
are the vertices of a parallelogram ABCD
∴ Diagonal AC and BD bisect each other at O
O is the midpoint of AC as well as BD
Let co-ordinates of O be (x, y)
When O is mid-point of AC, then

Again when O is the mid-point of BD

Then x = (1 + 1)/2 = 2/2 = 1

And y = (0 + q)/2 = q/2

Now comparing, we get

(p – 2)/2 = 1

⇒ p – 2 = 2

⇒ p = 2 + 2 = 4

∴ p = 4 and q/2 = 1

⇒ q = 2

Hence p = 4, q = 2

Question -21. If two vertices of a parallelogram are (3, 2) ( – 1, 0) and its diagonals meet at (2, – 5), find the other two vertices of the parallelogram.

Answer :

Two vertices of a ||gm ABCD are A (3, 2), B (-1, 0)
and point of intersection of its diagonals is P (2, -5)
P is mid-point of AC and BD.
Let co-ordinates of C be (x, y), then

2 = (x + 3)/2

⇒ x + 3 = 4

⇒ x = 4 – 3 = 1

And – 5 = (y + 2)/2

⇒ y + 2 = – 10

⇒ y = – 10 – 2 = – 12

∴ Co-ordinates of C are (1, – 12)

Similarly we shall find the co-ordinates of D also

2 = (x – 1)/2

⇒ x – 1 = 4

⇒ x = 4 + 1 = 5

– 5 = (y + 0)/2

⇒ – 10 = y

∴ Co-ordinates of D are (5, – 10)

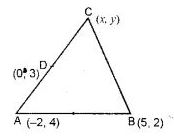
Question-22. Find the third vertex of a triangle if its two vertices are ( – 1, 4) and (5, 2) and mid point of one sides is (0, 3).

Answer:

Let A (-1, 4) and B (5, 2) be the two points and let D (0, 3)
be its the midpoint of AC and co-ordinates of C be (x, y).

∴ 0 = (x – 1)/2

⇒ x – 1 = 0

⇒ x = 1

3 = (y + 4)/2

⇒ y + 4 = 6

⇒ y = 6 – 4 = 2

∴ Co-ordinates of will be (1, 2)

If we take mid-point D (0, 3) of BC, then

0 = (5 + x)/2

⇒ x + 5 = 0

⇒ x = – 5

and 3 = (2 + y)/2

⇒ 2 + y = 6

⇒ y = 6 – 2 = 4

∴ Co-ordinates of C will be (-5, 4)

Hence co-ordinates of C, third vertex will be (1, 2) or (5, -4)

Question -23. Find the coordinates of the vertices of the triangle the middle points of whose sides are (0,1/2),(1/2,1/2), and (1/2,0)

Answer :

Let ABC be a ∆ in which (0,1/2),(1/2,1/2), and (1/2,0),
the mid-points of sides AB, BC and CA respectively.
Let co-ordinates of A be (x₁, y₁), B (x₂, y₂), C (x₃, y₃)

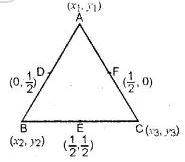
(x₁ + x₂)/2

⇒ x₁ + x₂ = 0 …(i)

1/2 = (y₁ + y₂)/2

⇒ y₁ + y₂ = 1 …(ii)

Again 1/2 = (x₂ + x₃)/2

⇒x₂ + x₃ = 1 …(iii)

And 1/2 = (y₂ + y₃)/2

⇒y₂ + y₃ = 1 …(iv)

And 1/2 = (x₃ + x₁)/2

⇒ x₃ + x₁ = 1 …(v)

0 = (y₃ + y₁)/2

⇒ y₃ + y₁ = 0 …(vi)

Adding (i), (iii) and (v)

2(x₁ + x₂ + x₃) = 0 + 1 + 1 = 2

∴ x₁ + x₂ + x₃ = 1

Now substituting (iii), (v) and (i) respectively, we get

x₁ = 0, x₂ = 0, x₃ = 1

Again Adding (ii), (iv) and (vi)

2 (y₁ + y₂ + y₃) = 1 + 1 + 0 = 2

∴ y₁ + y₂ + y₃ = 1

Now subtracting (iv), (vi) and (ii) respectively we get,

y₁ = 0, y₂ = 1, y₃ = 0

∴ Co-ordinates of A, B and C will be (0, 0), (0, 1) and (1, 0)

Question-24. Show by section formula that the points (3, – 2), (5, 2) and (8, 8) are collinear.

Answer :

Let the point (5, 2) divides the line joining the points (3, -2) and (8, 8)
in the ratio of m₁ : m₂

∴ 5 = (m₁ × 8 + m₂ × 3)/(m₁ + m₂)

⇒ 8m₁ + 3m₂ = 5m₁ + 5m₂

⇒ 8m₁ – 5m₁

⇒ 5m₂ – 3m₂

⇒ 3m₁ = 2m₂

⇒ m₁/m₂ = 2/3 ….(i)

Again 2 = (8m₁ – 2m₂)/(m₁+m₂)

⇒ 8m₁ – 2m₂ = 2m₁ + 2m₂

⇒ 8m₁ – 2m₁ = 2m₂ + 2m₂

⇒ 6m₁ = 4m₂

⇒ m₁/m₂ = 4/6 = 2/3 …(ii)

From (i) and (ii) it is clear that point (5, 2) lies on the line joining the points (3, – 2) and (8, 8).

Hence, proved.

Question -25. Find the value of p for which the points ( – 5, 1), (1, p) and (4, – 2) are collinear.

Answer:

Let points A (-5, 1), B (1, p) and C (4, -2)
are collinear and let point A (-5, 1) divides
BC in the ratio in m₁ : m₂

∴ x = (m₁x₂ + m₂x₁)/(m₁ + m₂)

⇒ -5 = (m₁×4 + m₁×1)/(m₁ + m₂) = (4m₁ + m₂)/(m₁ + m₂)

⇒ – 5m₁ – 5m₂ = 4m₁ + m₂

⇒ – 5m₁ – 4m₁ = m₂ + 5m₂

⇒ – 9m₁ = 6m₂

⇒ m₁/m₂ = 6/-9 = 2/-3 …(i)

And {m₁×(-2) + m₂×p}/(m₁+m₂)

= (-2m₁ + m₂p)/(m₁+m₂)

⇒ m₁ + m₂ = -2m₁ + m₂p

⇒ m₁ + 2m₁ = m₂p – m₂

⇒ 3m₁ – m₂ (p – 1)

⇒ m₁/m₂ = (p – 1)/3 …(ii)

From (i) and (ii)

(p – 1)/3 = 2/(-3)

⇒ – 3p + 3 = 6

⇒ – 3p = 6 – 3

⇒ – 3p = 3

⇒ p = 3/-3

= – 1

Question -26. The mid-point of the line segment AB shown in the adjoining diagram is (4, – 3). Write down die co-ordinates of A and B.

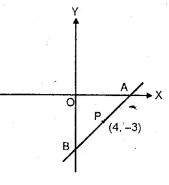
Answer :

A lies on x-axis and B on the y-axis.
Let co-ordinates of A be (x, 0) and of B be (0, y)
P (4, -3) is the mid-point of AB

∴ 4 = (x + 0)/2

⇒ x = 8

And – 3 = (0 + y)/2

⇒ y = – 6

Co-ordinates of A will be (8, 0) and of B will be (0, – 6)

---

ML Aggarwal Section Formula Exe-11 Solutions

ICSE Class-10 Maths Ch-11

Page-224

Question -27. Find the co-ordinates of the centroid of a triangle whose vertices are A ( – 1, 3), B(1, – 1) and C (5, 1) (2006)

Answer :

Co-ordinates of the centroid of a triangle,

whose vertices are (x1, y1), (x2, y2) and

(x₃, y₃) are {(x₁ + x₂ + x₃)/3 , (y₁ + y₂ + y₃)/3}

∴ Co-ordinates of the centroid of the given triangle are {(-1 + 1 + 5)/3, (3 – 1 + 1)/2} i.e., (5/3, 1)

Question -28. Two vertices of a triangle are (3, – 5) and ( – 7, 4). Find the third vertex given that the centroid is (2, – 1).

Answer :

Let the co-ordinates of third vertices be (x, y)
and other two vertices are (3, -5) and (-7, 4)
and centroid = (2, -1).

∴ 2 = (3 – 7 + x)/3

⇒ (x – 4)/3 = 2

x – 4 = 6

⇒ x = 6 + 4

⇒ x = 10

And ⇒ – 1 = (- 5 + 4 + y)/3

⇒ – 3 = – 1 + y

⇒ y = – 3 + 1

= 2

∴ Co-ordinates are (10, – 2)

Question -29 . The vertices of a triangle are A ( – 5, 3), B (p – 1) and C (6, q). Find the values of p and q if the centroid of the triangle ABC is the point (1, – 1).

Answer :

The vertices of ∆ABC are A (-5, 3), B (p, -1), C (6, q)
and the centroid of ∆ABC is O (1, -1)
co-ordinates of the centroid of ∆ABC will be

[(-5 + p + 6)/3, (3–1+q)/3]

⇒ {(1+p)/3, (2+q)/3}

But centroid is given (1, -1)

∴ Comparing, we get (1 + p)/3 = 1

⇒ 1 + p = 1

⇒ 1 + p = 3

⇒ p = 3 – 1 = 2

And (2 + q)/3 = – 1

⇒ 2 + q = – 3

⇒ q = – 3 – 2

⇒ q = – 5

Hence,

p = 2, q = – 5

—  : End of ML Aggarwal Section Formula Exe-11 Solutions ICSE Class-10 Maths Ch-11 : –

Return to :- ML Aggarwal Solutions for ICSE Class-10

Thanks

Please Share with Your Friends