Selina Concise Class-9th Mid Point and Intercept Theorem ICSE Mathematics Solutions Chapter-12. We provide step by step Solutions of Exercise / lesson-12 Mid Point and its Converse ( Including Intercept Theorem ) for ICSE Class-9 Concise Selina Mathematics by R K Bansal.
Our Solutions contain all type Questions with Exe-12 A and Exe-12 B, to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-9 Mathematics .
Selina Concise Class-9th Mid Point and Intercept Theorem ICSE Mathematics Solutions Chapter-12
–: Select Topic :–
Exercise – 12 A, Selina Concise Class-9th Mid Point and its Converse ( Including Intercept Theorem ) ICSE Mathematics Solutions
Question 1
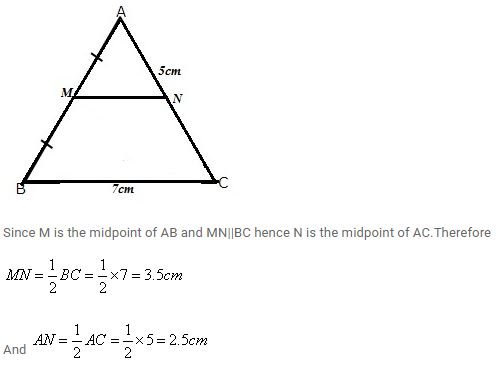
In triangle ABC, M is mid-point of AB and a straight line through M and parallel to BC cuts AC in N. Find the lengths of AN and MN if Bc = 7 cm and Ac = 5 cm.
Answer
The triangle is shown below,
Question 2
Prove that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
Answer
The figure is shown below,
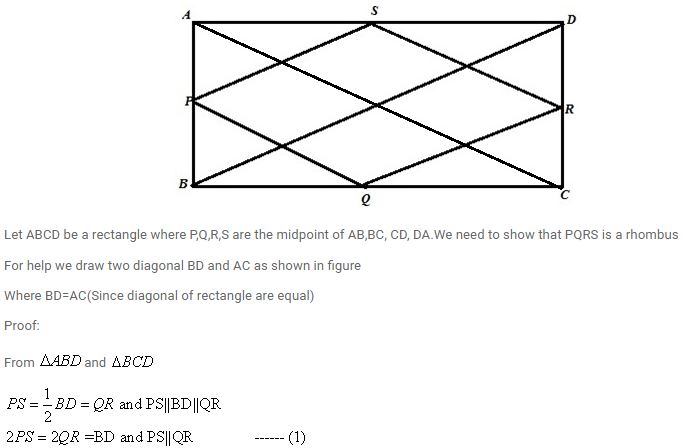
Similarly 2PQ=2SR=AC and PQ||SR—– (2)
From (1) and (2) we get
PQ=QR=RS=PS
Therefore PQRS is a rhombus.
Hence proved
Question 3
D, E and F are the mid-points of the sides AB, BC and CA of an isosceles ΔABC in which AB = BC. Prove that ΔDEF is also isosceles.
Answer
The figure is shown below
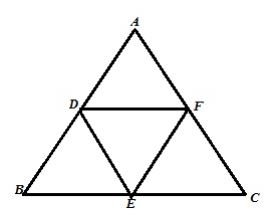
Given that ABC is an isosceles triangle where AB=AC.
Since D,E,F are midpoint of AB,BC,CA therefore
2DE=AC and 2EF=AB this means DE=EF
Therefore DEF is an isosceles triangle an DE=EF.
Hence proved
Question 4
The following figure shows a trapezium ABCD in which AB // DC. P is the mid-point of AD and PR // AB. Prove that:
…………………
Answer
Here from triangle ABD P is the midpoint of AD and PR||AB, therefore Q is the midpoint of BD
Similarly R is the midpoint of BC as PR||CD||AB
From triangle ABD 2PQ=AB …….(1)
From triangle BCD 2QR=CD …..(2)
Now (1)+(2)=>
2(PQ+QR)=AB+CD
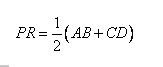
Hence proved
Question 5
The figure, given below, shows a trapezium ABCD. M and N are the mid-point of the non-parallel sides AD and BC respectively. Find:
……………
(i) MN, if AB = 11 cm and DC = 8 cm.
(ii) AB, if Dc = 20 cm and MN = 27 cm.
(iii) DC, if MN = 15 cm and AB = 23 cm.
Answer
Let we draw a diagonal AC as shown in the figure below,

Question 6
The diagonals of a quadrilateral intersect at right angles. Prove that the figure obtained by joining the mid-points of the adjacent sides of the quadrilateral is rectangle.
Answer
The figure is shown below

Question 7
L and M are the mid-point of sides AB and DC respectively of parallelogram ABCD. Prove that segments DL and BM trisect diagonal AC.
Answer
The required figure is shown below
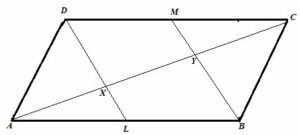
From figure,
BL=DM and BL||DM and BLMD is a parallelogram, therefore BM||DL
From triangle ABY
L is the midpoint of AB and XL||BY, therefore x is the midpoint of AY.ie AX=XY …..(1)
Similarly for triangle CDX
CY=XY …..(2)
From (1) and (2)
AX=XY=CY and AC=AX+XY+CY
Hence proved
Question 8
ABCD is a quadrilateral in which AD = BC. E, F, G and H are the mid-points of AB, BD, CD and Ac respectively. Prove that EFGH is a rhombus.
……………………..
Answer
Given that AD=BC …..(1)
From the figure,
For triangle ADC and triangle ABD
2GH=AD and 2EF=AD, therefore 2GH=2EF=AD …..(2)
For triangle BCD and triangle ABC
2GF=BC and 2EH=BC, therefore 2GF=2EH=BC …..(3)
From (1),(2),(3) we get,
2GH=2EF=2GF=2EH
GH=EF=GF=EH
Therefore EFGH is a rhombus.
Hence proved
Question 9
A parallelogram ABCD has P the mid-point of Dc and Q a point of Ac such that CQ = 1/4 AC. PQ produced meets BC at R.
Prove that
(i)R is the midpoint of BC
(ii)……….
Answer
For help we draw the diagonal BD as shown below

Question 10
D, E and F are the mid-points of the sides AB, BC and CA respectively of ABC. AE meets DF at O. P and Q are the mid-points of OB and OC respectively. Prove that DPQF is a parallelogram.
Answer
The required figure is shown below
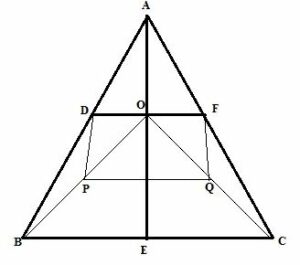
For triangle ABC and OBC
2DE=BC and 2PQ=BC, therefore DE=PQ …..(1)
For triangle ABO and ACO
2PD=AO and 2FQ=AO, therefore PD=FQ …..(2)
From (1),(2) we get that PQFD is a parallelogram.
Hence proved
Question 11
In triangle ABC, P is the mid-point of side BC. A line through P and parallel to CA meets AB at point Q; and a line through Q and parallel to BC meets median AP at point R. Prove that
(i)AP=2AR
(ii)BC=4QR
Answer
The required figure is shown below

Question 12
In trapezium ABCD, AB is parallel to DC; P and Q are the mid-points of AD and BC respectively. BP produced meets CD produced at point E. Prove that:
(i) Point P bisects BE,
(ii) PQ is parallel to AB.
Answer
The required figure is shown below
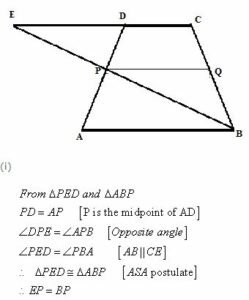
(ii)For tiangle ECB PQ||CE
Again CE||AB
Therefore PQ||AB
Hence proved
Question 13
In a triangle ABC, AD is a median and E is mid-point of median AD. A line through B and E meets AC at point F.
Prove that: AC = 3AF
Answer
The required figure is shown below
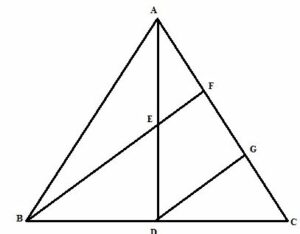
For help we draw a line DG||BF
Now from triangle ADG, DG||BF and E is the midpoint of AD
Therefore F is the midpoint of AG,ie AF=GF …..(1)
From triangle BCF, DG||BF and D is the midpoint of BC
Therefore G is the midpoint of CF,ie GF=CF …(2)
AC=AF+GF+CF
AC=3AF(From (1) and (2))
Hence proved
Question 14
D and F are mid-points of sides AB and AC of a triangle ABC. A line through F and parallel to AB meets BC at point E.
(i) Prove that BDFE is parallelogram
(ii) Find AB, if EF = 4.8 cm.
Answer
The required figure is shown below

Question 15
In triangle ABC, AD is the median and DE, drawn parallel to side BA, meets AC at point E. Show that BE is also a median.
Answer

Question 16
In ∆ABC, E is mid-point of the median AD and BE produced meets side AC at point Q. Show that BE : EQ = 3:1.
Answer

Question 17
In the given figure, M is mid-point of AB and DE, whereas N is mid-point of BC and DF. Show that: EF = AC.
Answer

Selina Concise Class-9th Mid Point and Intercept Theorem ICSE Mathematics Solutions Exercise – 12 B
Question 1
Use the following figure to find:
(i) BC, if AB = 7.2 cm.
(ii) GE, if FE = 4 cm.
(iii) AE, if BD = 4.1 cm
(iv) DF, if CG = 11 cm.
Answer
According to equal intercept theorem since CD=DE
Therefore AB=BC and EF=GF
(i)BC=AB=7.2cm
(ii)GE=EF+GF=2EF==8cm
Since B,D,F are the midpoint and AE||BF||CG
Therefore AE=2BD and CG=2DF

Question 2
In the figure, give below, 2AD = AB, P is mid-point of AB, Q is mid-point of DR and PR // BS. Prove that:
(i) AQ // BS
(ii) DS = 3 Rs.
Answer
Given that AD=AP=PB as 2AD=AB and p is the midpoint of AB
(i)From triangle DPR, A and Q are the midpoint of DP and DR.
Therefore AQ||PR
Since PR||BS ,hence AQ||BS
(ii)From triangle ABC, P is the midpoint and PR||BS
Therefore R is the midpoint of BC

Question 3
The side AC of a triangle ABC is produced to point E so that CE = 1/2AC. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meet AC at point P and EF at point R respectively. Prove that:
(i) 3DF = EF(ii) 4CR = AB.
Answer
Consider the figure:

Question 4
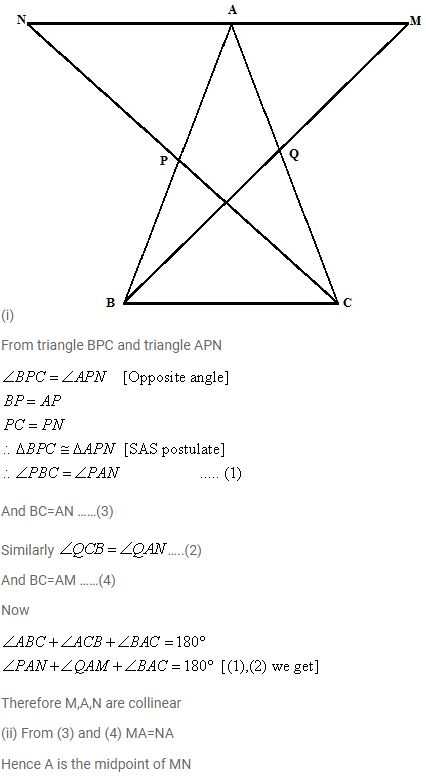
In triangle ABC, the medians BP and CQ are produced upto points M and N respectively such that BP = PM and CQ = QN. Prove that:
(i) M, A and N are collinear.
(ii) A is the mid-point of MN
Answer
The figure is shown below
Question 5
In triangle ABC, angle B is obtuse. D and E are mid-points of sides AB and BC respectively and F is a point on side AC such that EF is parallel to AB. Show that BEFD is a parallelogram.
Answer
The figure is shown below
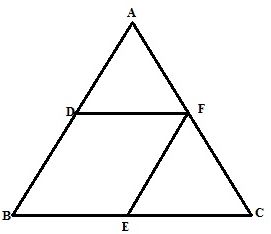
From the figure EF||AB and E is the midpoint of BC.
Therefore F is the midpoint of AC.
Here EF||BD, EF=BD as D is the midpoint of AB
BE||DF, BE=DF as E is the midpoint of BC.
Therefore BEFD is a parallelogram.
Question 6
In parallelogram ABCD, E and F are mid-points of the sides AB and CD respectively. The line segments AF and BF meet the line segments ED and EC at points G and H respectively. Prove that:
(i) Triangles HEB and FHC are congruent;
(ii) GEHF is a parallelogram.
Answer
The figure is shown below
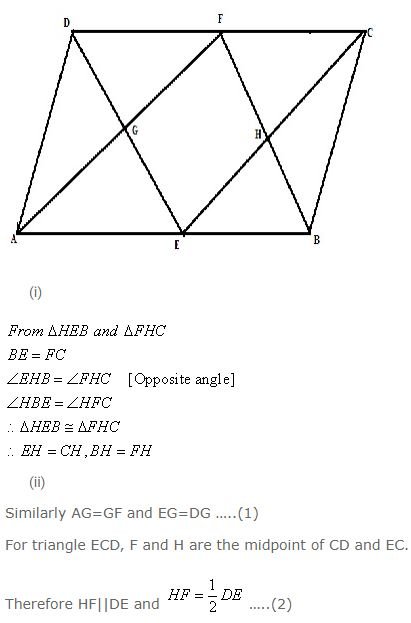
(1),(2) we get, HF=EG and HF||EG
Similarly we can show that EH=GF and EH||GF
Therefore GEHF is a parallelogram.
Question 7
In triangle ABC, D and E are points on side AB such that AD = DE = EB. Through D and E, lines are drawn parallel to BC which meet side AC at points F and G respectively. Through F and G, lines are drawn parallel to AB which meet side BC at points M and N respectively. Prove that: BM = MN = NC.
Answer
The figure is shown below
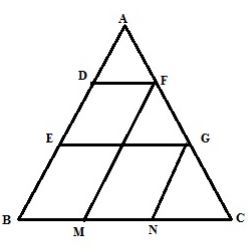
For triangle AEG
D is the midpoint of AE and DF||EG||BC
Therefore F is the midpoint of AG.
AF=GF …..(1)
Again DF||EG||BC DE=BE, therefore GF=GC …..(2)
(1),(2) we get AF=GF=GC.
Similarly Since GN||FM||AB and AF=GF ,therefore BM=MN=NC
Hence proved
Question 8
In triangle ABC; M is mid-point of AB, N is mid-point of AC and D is any point in base BC. Use intercept Theorem to show that MN bisects AD.
Answer
The figure is shown below
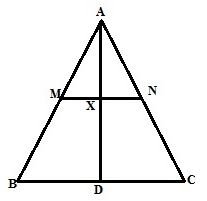
Since M and N are the midpoint of AB and AC, MN||BC
According to intercept theorem Since MN||BC and AM=BM,
Therefore AX=DX. Hence proved
Question 9
If the quadrilateral formed by joining the mid-points of the adjacent sides of quadrilateral ABCD is a rectangle, show that the diagonals AC and BD intersect at right angle.
Answer
The figure is shown below
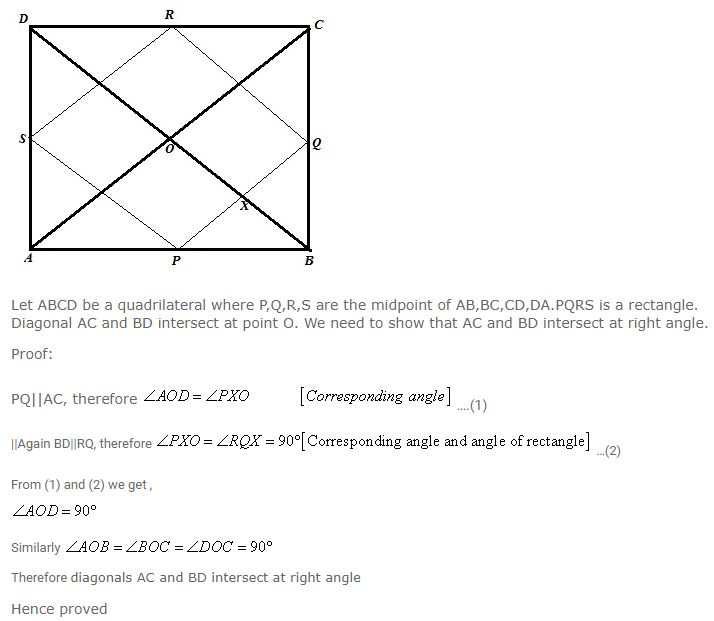
Question 10
In triangle ABC; D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F. Prove that BDEF is a parallelogram. If AB = 16 cm, AC = 12 cm and BC = 18 cm, find the perimeter of the parallelogram BDEF.
Answer
The figure is shown below

Question 11
In the given figure, AD and CE are medians and DF//CE. Prove that: ………
………………
Answer
Given AD and CE are medians and DF || CE.
We know that from the midpoint theorem, if two lines are parallel and the starting point of segment is at the midpoint on one side, then the other point meets at the midpoint of the other side.
Consider triangle BEC. Given DF || CE and D is midpoint of BC. So F must be the midpoint of BE.
Question 12
In parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P.
Prove that:
(i) BP = 2AD
(ii) O is the mid-point of AP.
………………
Answer
Given ABCD is parallelogram, so AD = BC, AB = CD.
Consider triangle APB, given EC is parallel to AP and E is midpoint of side AB. So by midpoint theorem, C has to be the midpoint of BP.
So BP = 2BC, but BC = AD as ABCD is a parallelogram.
Hence BP = 2AD
Consider triangle APB, AB || OC as ABCD is a parallelogram. So by midpoint theorem, O has to be the midpoint of AP.
Hence Proved
Question 13
In trapezium ABCD, sides AB and DC are parallel to each other. E is mid-point of AD and F is mid-point of BC. Prove that: AB + DC = 2EF.
Answer
Consider trapezium ABCD.
Given E and F are midpoints on sides AD and BC, respectively.

We know that AB = GH = IJ
From midpoint theorem,
Consider LHS,
AB + CD = AB + CJ + JI + ID = AB + 2HF + AB + 2EG
So AB + CD = 2(AB + HF + EG) = 2(EG + GH + HF) = 2EF
AB + CD = 2EF
Hence Proved
Question 14
In Δ ABC, AD is the median and DE is parallel to BA, where E is a point in AC. Prove that BE is also a median.
Answer
Given Δ ABC
AD is the median. So D is the midpoint of side BC.
Given DE || AB. By the midpoint theorem, E has to be midpoint of AC.
So line joining the vertex and midpoint of the opposite side is always known as median. So BE is also median of Δ ABC.
Question 15
Adjacent sides of a parallelogram are equal and one of the diagonals is equal to any one of the sides of this parallelogram. Show that its diagonals are in the ratio.
Answer
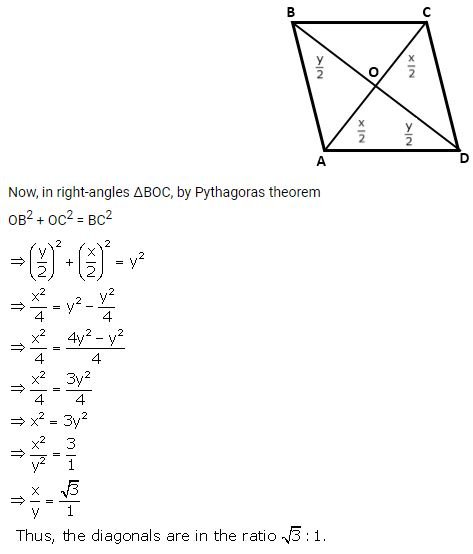
— End of Mid Point and its Converse ( Including Intercept Theorem ) Solutions :–
Return to – Concise Selina Maths Solutions for ICSE Class -9
Thanks