Sets Class 11 OP Malhotra Exe-1K ISC Maths Solutions. In this article you would learn about More Practical Problems. Step by step solutions of latest textbook has been given as latest syllabus. Visit official Website CISCE for detail information about ISC Board Class-11 Mathematics.

Sets Class 11 OP Malhotra Exe-1K ISC Maths Solutions Ch-1
| Board | ISC |
| Publications | S Chand |
| Subject | Maths |
| Class | 11th |
| Chapter-1 | Sets |
| Writer | OP Malhotra |
| Exe-1(K) | More Practical Problems. |
Exercise- 1K
Sets Class 11 OP Malhotra Exe-1K ISC Maths Solutions
Que-1: In a survey it was found that 21 people liked product A, 26 liked product B and 29 liked product C. If 14 people liked products A and B, 12 people liked products C and A, 14 people liked products B and C and 8 liked all the three products, find how many liked product C only.
Sol: Let A be the set of people who liked product A.
B be the set of people who liked product B.
C be the set of people who liked product C.
It is given that
n (A) = 21, n (B) = 26, n (C) = 29, n (A ∩ B) = 14, n (A ∩ C) = 12, n (B ∩ C) = 14, n (A ∩ B ∩ C) = 8
Let’s draw the Venn diagram for the given problem
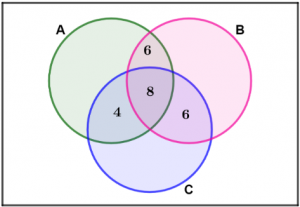
We can see that
Number of people who like product C only
= n (C) – (4 + 8 + 6)
= 29 – 18
= 11
Hence, 11 students liked product C only
Que-2: In a survey of 200 students of a school, it was found that 120 study. Mathematics, 90 study Physics and 70 study Chemistry, 40 study Mathematics and Physics, 30 study Physics and Chemistry, 50 study Chemistry and Mathematics and 20 none of these subjects.
(i) Find the number of students who study all three subjects.
(ii) Also, find the number of students who study Mathematics only.
Sol: Given : Total number of students = 200
Number of students study Mathematics = 120
Number of students study Physics = 90
Number of students study Chemistry = 70
Number of students study Mathematics and Physics = 40
Number of students study Mathematics and Chemistry = 50
Number of students study Physics and Chemistry = 30
Number of students study none of them = 20
Let U be the total number of students, P, M and C be the number of students study Physics, Mathematics and Chemistry respectively
(i) Number of students who play either of them = n(P ∪ M ∪ C)
= Total – None of them
= 200 – 20
= 180 ……..(i)
Number of students who play either of them = n(P ∪ M ∪ C)
= n(C) + n(P) + n(M) – n(M ∩ P) – n(M ∩ C) – n(P ∩ C) + n(P ∩ M ∩ C)
= 120 + 90 + 70 – 40 – 30 – 50 + n(P ∩ M ∩ C)
= 160 + n(P ∩ M ∩ C) …….(ii)
From (i) and (ii)
160 + n(P ∩ M ∩ C) = 180
⇒ n(P ∩ M ∩ C) = 180 – 160
⇒ n(P ∩ M ∩ C) = 20
(ii) Only Math = n(M) − n(M∩P) − n(M∩C) + n(M∩P∩C) Only Mat
= 120 − 40 − 50 + 20
= 50.
Que-3: In a group of 500 person, 300 take tea, 150 take coffee, 250 take cold drink, 90 take tea and coffee, 110 take tea and cold drink, 80 take coffee and cold drink and 50 take all three drinks.
(i) Find the number of persons who take none of the three drinks.
(ii) Find the number of persons who take only tea.
(iii) Find the number of persons who take coffee and cold drink but not tea.
Sol: Given :
n(u) = 500, n(T) = 300,
n(Co) = 150, n(Cd) = 250,
n(T ∩ Co) = 90, n(T ∪ Cd) = 110,
n(Co ∩ Cd) = 80, n(T ∩ Cd ∩ Co) = 50
(i) Number of persons who take none of three drinks
n(u)n(T ∪ Co ∪ Cd)
{n(T) = like tea}
{n(Co) = like Coffee}
{n(Cd) = like Cold drink}
n(T ∪ Co ∪ Cd) = n(T)) + n(Co) n(Cd) − n(T ∩ Co) −n(T ∩ Cd)
= n(C ∩ Cd) + n(T ∩ Cd ∩ Co]
= 300 + 150 + 250-90-110-80 + 50
= 750 – 280
= 470
n(u) − n(T ∪ Co ∪ Cd)
= 500 − 470
= 30
∴ Number of persons who take none of three drinks = 30.
(ii) Number of person who take only tea
n(T) − n(T ∩ Co) − n(T ∩ Cd) + n(T ∩ Cd ∩ Co)
= 300 – 90 – 110 + 50
= 350 – 200
= 150
∴ Number of person who take only tea = 150
(iii) Number of persons who take coffee and cold drink but not tea
n(Co ∩ Cd) − n(T ∩ Co ∩ Cd)
= 80 – 50
= 30
∴ Number of persons who take coffee and cold drink but not tea = 30.
Que-4: In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows : French 17, English 13, Sanskrit 15, French and English 9, English and Sanskrit 4, French and Sanskrit 5,English, French and Sanskrit 3. Find the number of students who study (i) Only French (ii) Only English (iii) Only Sanskrit (iv) English and Sanskrit but not French (v) French and Sanskrit but not English (vi) French and English but not Sanskrit (vii) At least one of the three languages (viii) None of the three languages
Sol: Given :
n(F) = 17
n(E) = 13
n(S) = 15
n(F∩E) = 9
n(E∩S) = 4
n(F∩S) = 5
n(F∩E∩S) = 3
Total students = 50
Let :
a: Only French
b: Only English
c: Only Sanskrit
d: French and English only
e: English and Sanskrit only
f: French and Sanskrit only
g: All three languages
h: None
From intersections:
d+g = n(F∩E) = 9
⇒ d = 9−g = 9−3 = 6
e+g = n(E∩S) = 4
⇒ e = 4−3 = 1
f+g = n(F∩S) = 5
⇒ f = 5−3 = 2
Now compute a, b, c using total counts:
a = n(F)−d−f−g = 17−6−2−3 = 6
b = n(E)−d−e−g = 13−6−1−3 = 3
c = n(S)−e−f−g = 15−1−2−3 = 9
Now compute total of all who study at least one language:
a + b + c + d + e + f + g
= 6 + 3 + 9 + 6 + 1 + 2 + 3 = 30
h = 50−30 = 20
(i) Only French = a = 6
(ii) Only English = b = 3
(iii) Only Sanskrit = c = 9
(iv) English and Sanskrit but not French = e = 1
(v) French and Sanskrit but not English = f = 2
(vi) French and English but not Sanskrit = d = 6
(vii) At least one of the three languages = a+b+c+d+e+f+g = 30
(viii) None of the three languages = h = 20.
Que-5: In a survey it was found that 21 persons liked product P1, 26 liked product P2 and 29 liked product P3. If 14 persons liked product P1 and P2, 12 persons liked products P1 and P3, 14 persons liked products P2 and P3 and 8 liked all the three products, then how many liked only one product ?
Sol: Given :
n(P1) = 21
n(P2) = 26
n(P3) = 29
n(P1∩P2) = 14
n(P1∩P3) = 12
n(P2∩P3) = 14
n(P1∩P2∩P3) = 8
Let :
: Only P1
b: Only P2
c: Only P3
d: P1 and P2 only
e: P1 and P3 only
f: P2 and P3 only
g: All three (P1, P2, P3) = 8
d = n(P1∩P2) − g = 14 − 8 = 6
e = n(P1∩P3) − g = 12 − 8 = 4
f = n(P2∩P3) − g = 14 − 8 = 6
a = n(P1) − d − e − g
= 21 − 6 − 4 − 8 = 3
b = n(P2) − d − f − g
= 26 − 6 − 6 − 8 = 6
c = n(P3) − e − f − g
= 29 − 4 − 6 − 8 = 11
Only one product = a + b + c = 3 + 6 + 11 = 20
Que-6: In a survey of 100 persons it was found that 28 read magazine A, 30 read magazine B, 42 read magazine C, 8 read magazines A and B, 10 read magazines A and C, 5 read magazines B and C and 3 read all the three magazines. (i) How many persons read none of the three magazines?
(ii) How many persons read magazine C only?
Sol: Let A, B C be the sets of the persons who read magazines A, B and C, respectively. Also, let U denote the universal set.
We have: n(U) = 100
n(A) = 28, n(B) = 30, n(C) = 42, n(A∩B) = 8, n(A∩C) = 10, n(B∩C) = 5 and n(A∩B∩C) = 3
Now,
(i) Number of persons who read none of the three magazines = n(A′∩B′∩C′)
= n(U) −n(A∪B∪C)
= n(U) −{n(A) + n(B) + n(C)
= n(A∩B) −n(A∩C) −n(B∩C) + n(A∩B∩C)}
= 100 −(28 + 30 + 42 − 8−10 −5 + 3)
= 20
(ii) Number of students who read magazine C only = n(C∩A′∩B′)
= n{C∩(A∪B)′}
= n(C) −n{C∩(A∪B)}
= n(C) −n{(C∩A)∪(C∩B)}
= n(C) −n{(C∩A) + (C∩B)−(A∩B∩C)}
= 42−(10 + 5−3)
= 30
–: End of Sets Class 11 OP Malhotra Exe-1K ISC Maths Solutions :–
Return to :- OP Malhotra ISC Class-11 S Chand Publication Maths Solutions
Thanks
Please share with your friends


