Sets ICSE Class-8th Concise Selina Maths Solutions Chapter-6. We provide step by step Solutions of Exercise / lesson-6 Sets for ICSE Class-8 Concise Selina Mathematics. Our Solutions contain all type Questions with Exe-6 A, Exe-6 B, Exe-6 C, Exe-6 D and Exe-6 E, to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-8.
Sets ICSE Class-8th Concise Selina Maths Solutions Chapter-6
–: Select Topics :–
Exercise – 6 A Sets ICSE Class-8th Concise Selina Solutions
Question 1 :-
Write the following sets in roster (Tabular) form :
(i) A1 = {x : 2x + 3 = 11}
(ii) A2 = {x : x2 – 4x – 5 = 0}
(iii) A3 = {x : x ∈ Z, -3 ≤ x < 4}
(iv) A4 = {x : x is a two digit number and sum of digits of x is 7}
(v) A5 = {x : x = 4n, n ∈ W and n < 4}
(vi) A6 = {x : x = ; n ∈ N and n > 5}
Answer :-

(iv) A4 = {x : x is a two digit number and sum of digits of x is 7}
A4 = {x : x is a two digit number and sum of digits of x is 7}
∵ x is a two digit number and sum of digits of x is 7
∴ x = 16, 25, 34, 43, 52, 61, 70
∴ Given set in roster (Tabular) form is
A4 = {16, 25, 34, 43, 52, 61, 70}
(v) A5 = {x : x = 4n, n ∈ W and n < 4}
A5 = {x : x = 4n, n ∈ W and n < 4}
∵ x = 4n
∴ When n = 0,
x = 4 x 0
⇒ x = 0
When n = 1,
x = 4 x 1
⇒ x = 4
When n = 2,
x = 4 x 2
⇒ x = 8
When n = 3,
x = 4 x 3
⇒ x = 12
∴ Given set in roster (Tabular) form is
A5 = {0, 4, 8, 12}

Question 2 :-
Write the following sets in set-builder (Rule Method) form :

Answer :-

Question 3 :-
(i) Is {1, 2, 4, 16, 64} = {x : x is a factor of 32} ? Give reason.
(ii) Is {x : x is a factor of 27} ≠ {3, 9, 27, 54} ? Give reason.
(iii) Write the set of even factors of 124.
(iv) Write the set of odd factors of 72.
(v) Write the set of prime factors of 3234.
(vi) Is {x : x2 – 7x + 12 = 0} = {3, 4} ?
(vii) Is {x : x2 – 5x – 6 = 0} = {2, 3} ?
Answer :-
(i) No, {1, 2, 4, 16, 64} ≠ {x : x is factor of 32}
Because 64 is not a factor of 32
(ii)
Yes, {x : x is a factor of 27} + {3, 9, 27, 54}
Because 54 is not a factor of 27
(iii)
1 x 124 = 124
2 x 62 = 124
4 x 31 = 124
Factors of 124 = 1, 2, 4, 31, 62, 124
Set of even factors of 124 = {2, 4, 62, 124}
(iv)
1 x 72 = 72
2 x 36 = 72
3 x 24 = 72
4 x 18 = 72
6 x 12 = 72
8 x 9 = 72
Factors of 72 = 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Set of odd factors of 72 = {1, 3, 9}
(v)
| 2 | 3234 |
| 3 | 1617 |
| 7 | 539 |
| 7 | 77 |
| 11 |
3234 = 2 x 3 x 7 x 7 x 11
∴ Set of prime factors of 3234 = {2, 3, 7, 11}
(vi)
x2 – 7x + 12 = 0
⇒ x2 – 4x – 3x + 12 = 0
⇒ x (x – 4) – 3(x – 4) = 0
⇒ (x – 4) (x – 3) = 0
∴ Either x – 4 = 0
⇒ x = 4
Or
x – 3 = 0
⇒ x = 3
∴ {x : x2 – 7x + 12 = 0}
= {3, 4} is true.
(vii)
x5 – 5x – 6 = 0
⇒ x2 – 6x + x – 6 = 0
⇒ x (x – 6) + 1 (x – 6) = 0
⇒ (x – 6) (x – 1) = 0
∴ Either x – 6 = 0
i.e., x = 6
Or
x + 1 = 0
i.e. x = -1
∴ {x : x2 – 5x – 6 = 0} ≠ {2, 3}
In other words {x : x2 – 5x -6 = 0}
= {2, 3} is not true.
Question 4 :-
Write the following sets in Roster form :
(i) The set of letters in the word ‘MEERUT’.
(ii) The set of letters in the word ‘UNIVERSAL’.
(iii) A = {x : x = y + 3, y ∈N and y > 3}
(iv) B = {p : p ∈ W and p2 < 20}
(v) C = {x : x is composite number and 5 < x < 21}
Answer :-
(i) The set of letters in the word ‘MEERUT’.
Roster form of the set of letters in the word “MEERUT” = {m, e, r, u, t}
(ii) The set of letters in the word ‘UNIVERSAL’.
Roster form of the set of letters in the word “UNIVERSAL” = {u, n, i, v, e, r, s, a, l}
(iii) A = {x : x = y + 3, y ∈N and y > 3}
A = {x : x = y + 3, y ∈ N and y > 3}
x = y + 3
When y = 4,
When y = 5,
When y = 6,
When y = 7,
When y = 8,
………………………
………………………
x = 4+3 = 7
x = 5+3 = 8
x = 6+3 = 9
x = 7+3 = 10
x = 8+3 = 11
……………………….
……………………….
∴ Roster form of the given set A = {7, 8, 9, 10, 11 ………..}
(iv)
B = {p : p ∈ W and p2 < 20}
B = {P : P ∈ W and p2 < 20}
When p2 = 0
P = √0 = 0
When p2 = 1
P = √1 = 1
When p2 = 4
P = √4 = 2
When p2 = 9
P = √9 = 3
When p2 = 16
P = √16 = 4
∴ Roster form of the given set B = {0, 1, 2, 3, 4}
(v) C = {x : x is composite number and 5 < x < 21}
C = {x : x is composite number and 5 < x < 21}
5 ≤ x ≤ 21 means x = 5, 6, 7, 8, 9, 10 ……, 21
But we are given that x is a complete number
∴ x = 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21
∴ Roster form of the given set C = {6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21}
Note: Composite numbers : The natural numbers (greater than 1), which are not prime, are called composite numbers.
Question 5 :-
List the elements of the following sets :
(i) {x : x2 – 2x – 3 = 0}
(ii) {x : x = 2y + 5; y ∈ N and 2 ≤ y < 6}
(iii) {x : x is a factor of 24}
(iv) {x : x ∈ Z and x2 ≤ 4}
(v) {x : 3x – 2 ≤ 10, x ∈ N}
(vi {x : 4 – 2x > -6, x ∈ Z}
Answer :-
(i) {x : x2 – 2x – 3 = 0}
{x : x2 – 2x – 3 = 0}
x2 – 2x – 3 = 0
⇒ x2 – 3x + x – 3 = 0
⇒ x (x-3) + 1 (x-3) = 0
⇒ (x+1) (x – 3) = 0
∴ Either x – 3 = 0 x
x = 3
Or
x + 1 = 0
x = -1
∴ Elements of the set {x : x2 – 2x – 3 = 0} are 3 and -1
(ii) {x : x = 2y + 5; y ∈ N and 2 ≤ y < 6}
{x : x = 2y + 5; y ∈ N and 2 ≤ y < 6}
x = 2y + 5
When y = 2,
x = 2 x 2+5
= 4+5
= 9
When y = 3,
x = 2 x 3 + 5
= 6+5
= 11
When y = 4,
x = 2 x 4+5
= 8+5
= 13
When y = 5,
x = 2 x 5 + 5
= 10+5
= 15
∴ Elements of the given set {x : x = 2y + 5; y ∈ N and 2≤ y ≤6} are 9, 11, 13, 15
(iii) {x : x is a factor of 24}
{x : x is a factor of 24}
24 = 1 x 24
24 = 2 x 12
24 = 3 x 8
24 = 4 x 6
∴ Elements of the given set {x : x is a factor of 24} are 1, 2. 3, 4, 6, 8, 12, 24
(iv) {x : x ∈ Z and x2 ≤ 4}
{x : x ∈ Z and x2 ≤ 4}
When x2 = 4
x = ± √4 = ±2
When x2 = 1
x = ± √1 = ±1
When x2 = 0
x = √0 = 0
∴ Elements of the given set {x : x ∈ Z and x2 ≤ 4} are +2, -2, +1, -1, 0 or are -2, -1, 0, 1, 2
(v) {x : 3x – 2 ≤ 10, x ∈ N}
{x : 3x – 2 ≤ 10, x ∈ N}
3x – 2 ≤ 10
⇒ 3x ≤ 10 + 2
⇒ 3x ≤ 12
⇒ x ≤ 12/3
⇒ x ≤ 4
∴ Elements of the given set {x : 3x – 2 ≤ 10, x ∈ N} are 1, 2, 3 and 4
(vi {x : 4 – 2x > -6, x ∈ Z}
{x : 4 – 2x > -6, x ∈ Z}
4 – 2x >-6
-4 + 4 -2x > -6 -4
(Subtracting 4 from both sides)
-2x > -10
-2x + 2x + 10 > -10 + 2x + 10
[Adding 2x + 10 to both sides]
+10 > 2x
10/2 > x
5 > x
∴ Elements of the given set { x : 4 – 2x > – 6, x ∈ Z} are 4, 3, 2, 1, 0, -1…….
Exercise – 6 B Sets for ICSE Class-8th Maths Solutions Concise selina
Question 1 :-
Find the cardinal number of the following sets :
(i) A1 = {-2, -1, 1, 3, 5}
(ii) A2 = {x : x ∈ N and 3 ≤ x < 7}
(iii) A3 = {p : p ∈ W and 2p – 3 < 8}
(iv) A4 = {b : b ∈ Z and -7 < 3b – 1 ≤ 2}
Cardinal Number of a set; The number of elements in a set is called is Cardinal Number.
Answer :-
(i) A1 = {-2, -1, 1, 3, 5}
A1 = {-2, -1, 1, 3, 5}
Cardinal number of set A1 = 5
(ii) A2 = {x : x ∈ N and 3 ≤ x < 7}
A2 = {x : x ∈ N and 3 ≤ x <7}
= {3, 4, 5, 6}
∴ Cardinal number of set A2 = 4
(iii) A3 = {p : p ∈ W and 2p – 3 < 8}
A3 = {P : P ∈ W and 2P – 3 < 8}
2P – 2 < 8
⇒ 2P – 3 + 3 < 8 + 3
(Adding 3 to both sides)
⇒ 2P < 11
⇒ P < 11/2
(Dividing both sides by 2)
⇒ P < 5.5
∴ A3 = {0, 1, 2, 3, 4, 5}
∴ Cardinal number of set A3 = 6
(iv) A4 = {b : b ∈ Z and -7 < 3b – 1 ≤ 2}
A4 = {b : b ∈ Z and -7 < 3b -1 ≤ 2}
-7 < 3b – 1
⇒ -7+1 < 3b -1+1
(Adding 1 to both sides)
⇒ -6 < 3b
⇒ -6/3 < b
(Dividing both sides by 3)
⇒ – 2 < b
Again 3b – 1 ≤ 2
⇒ 3b -1 + 1 ≤ 2+1 (Adding 1 to both sides)
⇒ 3b ≤ 3
⇒ b ≤ 3/3
(Dividing both sides by 3)
⇒ b ≤ 1
∴ -2 ≤ b ≤ 1
∴ Given set A4 = {-1, 0, 1}
∴ Cardinal number of set A4 = 3
Question 2 :-
If P = {P : P is a letter in the word “PERMANENT”}. Find n (P).
Answer :-
P = (P : P is a letter in the word “PERMANENT”}
or P = {p, e, r, m, a, n, t)
n (P) = 7
Question 3 :-
State, which of the following sets are finite and which are infinite :
(i) A = {x : x ∈ Z and x < 10}
(ii) B = {x : x ∈ W and 5x -3 ≤ 20}
(iii) P = {y : y = 3x -2, x ∈ N & x > 5}
(iv) M = {r : r = 3/n; n ∈ W and 6 < n ≤ 15}
Answer :-
(i)
A = {x : x ∈ Z and x < 10}
= {….., -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
= {9, 8, 7, 6, 5, 4, 3, 2, 1, 0, -1, -2, -3, -4, …..}
∴ It is an infinite set.
(ii)
B = {x : x ∈ W and 5x -3 ≤ 20}
5x – 3 ≤ 20
⇒ 5x -3+3 ≤ 20+ 3 (Adding 3 to both sides)
⇒ 5x ≤ 20+ 3
⇒ 5x ≤ 23
⇒ x ≤ 23/5
(Dividing both sides by 5)
⇒ x ≤ 4.6
∴ B = {0, 1, 2, 3, 4}
∴ It is a finite set.
(iii)
P = {y : y = 3x -2, x ∈ N & x > 5}
y = 3x -2
When x = 6,
y = 3 x 6 – 2
= 18 – 2
= 16
When x = 7,
y = 3 x 7 – 2
= 21 – 2
= 19
When x =8,
y = 3 x 8 – 2
= 24 – 2
= 22
When x = 9,
y = 3 x 9 – 2
= 27 – 2
= 25
∴ P = {16, 19, 22, 25,….}
∴ It is an infinite set.
(iv)
M = {r : r = 3/n; n ∈ W and 6 < n ≤ 15}
r = 3/n
When n = 7,
r = 3/7
When n = 8,
r = 3/8
When n = 9,
r = 3/9
When n = 10,
r = 3/10
When n =11,
r = 3/11
When n = 12,
r = 3/12
When n = 13,
r = 3/13
When n = 14,
r = 3/14
When n = 15,
r = 3/15
∴ M = {3/7,3/8,3/9,3/10,3/11,3/12,3/13,3/14,3/15}
∴ It is a finite set.
Question 4 :-
Find, which of the following sets are singleton sets :
(i) The set of points of intersection of two non-parallel st. lines in the same plane
(ii) A = {x : 7x – 3 = 11}
(iii) B = {y : 2y + 1 < 3 and y ∈ W}
Note : A set, which has only one element in it, is called a SINGLETON or unit set.
Answer :-
(i)
The set of points of intersection of two non-parallel st. lines in the same plane……singleton set.
(ii)
A = {x : 7x – 3 = 11}
7x -3 = 11
⇒ 7x = 11 + 3
⇒ 7x = 14
⇒ x = 14/7 = 2
∴ A = {2}
Hence given set A is a singleton set.
(iii)
B = {y :2y + 1 < 3 and y ∈ W}
2y + 1 < 3
⇒ 2y + 1 – 1< 3 -1 (Subtracting 1 from both sides)
⇒ 2y < 2
⇒ y < 2/2 (Dividing both sides by 2)
⇒ y < 1
∴ B = {0}
Hence it is a singleton set.
Question 5 :-
Find, which of the following sets are empty :
(i) The set of points of intersection of two parallel lines.
(ii) A = {x : x ∈ N and 5 < x < 6}
(iii) B = {x : x2 + 4 = 0, x ∈ N}
(iv) C = {even numbers between 6 & 10}
(v) D = {prime numbers between 7 & 11}
Note : The set, which has no element in it, is called the empty or null set.
Answer :-
(i)
“The set of points of intersection of two parallel lines” is an empty set because two parallel lines do not intersect anywhere.
(ii)
A = {x : x ∈ N and 5 < x < 6}
As 5 < x ≤ 6
∴ x = 6
∴ A = {6}
Hence given set A is not an empty set.
(iii)
B = {x : x2 + 4 = 0, x ∈ N}
x2 + 4 = 0
⇒ x2 = -4
⇒ x = √-4 which is not a natural number.
But x ∈ N
∴ B = { }
∴ Given set B is an empty set.
(iv)
C = {Even numbers between 6 & 10}
∴ C = {8}
Hence it is not an empty set.
(v)
D = {Prime numbers between 7 & 11}
Because there is no prime number between 7 and 11.
∴ D = { }
Hence it is an empty set.
Question 6 :-
(i) Are the sets A = {4, 5, 6} and B = {x : x2 – 5x – 6 = 0} disjoint ?
(ii) Are the sets A = {b, c, d, e} and B = {x : x is a letter in the word ‘MASTER’} joint ?
Note :
(i) Two sets are said to be joint sets, if they have at least one element in common.
(ii) Two sets are said to be disjoint, if they have no element in common.
Answer :-
(i)
A = {4, 5, 6}
B = {x : x2 – 5x – 6 = 0}
x2 – 5x – 6 = 0
⇒ x2 – 6x + x -6 = 0
⇒ x(x – 6) +1(x – 6) = 0
⇒ (x – 6) (x+1) = 0
∴ Either x – 6 = 0x
⇒ x = 6
Or
x+1 = 0
⇒ x = -1
∴ B = {6, -1}
Hence set A and set B are not disjoint because these sets have element 6 in common.
(ii)
A = {b,c,d,e}
B = {x : x is a letter in the word “MASTER”}
∴ B = {m, a ,s, t, e, r}
Hence set A and set B are joint because these sets have element e in common.
Question 7 :-
State, whether the following pairs of sets are equivalent or not :
(i) A = {x : x ∈ N and 11 ≥ 2x – 1} and B = {y : y ∈ W and 3 ≤ y ≤ 9}
(ii) Set of integers and set of natural numbers.
(iii) Set of whole numbers and set of multiples of 3.
(iv) P = {5, 6, 7, 8} and M = {x : x ∈ W and x < 4}
Note : Two sets are said to be equivalent, if they contain the same number of elements.
Answer :-
(i)
A = {x : x ∈ N and 11 ≥ 2x -1}
11 ≥ 2x -1
⇒ 11 + 1 ≥ 2x -1+1
⇒ 12 ≥ 2x
⇒ 122 ≥ x
⇒ 6 ≥ x
∴ A = {1, 2, 3, 4, 5, 6}
∴ n(A) = 6
B = {y : y ∈ W and 3 ≤ y ≤ 9}
∵ 3 ≤ y ≤ 9
B = {3,4,5,6,7,8,9}
n (B) = 7
Cardinal number of set A = 6 and cardinal number of set B = 7
Set A and set B are not equivalent.
(ii)
Set of integers has infinite number of elements. Set of natural numbers has infinite number of elements.
Set of integers and set of natural numbers are equivalent because both these sets have infinite number of elements.
(iii)
Set of whole numbers, has infinite number of elements. Set of multiples of 3, has infinite number of element.
Set of whole numbers and set of multiples of 3 are equivalent because both these sets have infinite number of elements.
(iv)
P = {5,6,7,8}
n (P) = 4
M = {x : x ∈ W and x ≤ 4}
M = {0, 1, 2, 3, 4}
n (M) = 5
Now Cardinal number of set P = 4 and
Cardinal number of set M = 5
These sets are not equivalent.
Question 8 :-
State, whether the following pairs of sets are equal or not :
(i) A = {2, 4, 6, 8} and
B = {2n : n ∈ N and n < 5}
(ii) M = {x : x ∈ W and x + 3 < 8} and
N = {y : y = 2n – 1, n ∈ N and n < 5}
(iii) E – {x : x2 + 8x – 9 = 0} and
F = {1, -9}
(iv) A = {x : x ∈ n, x < 3} and
B = {y : y2 – 3y + 2 = 0}
Note: Two sets are equal, if both the sets have same (identical) elements.
Answer :-
(i)
A = {2, 4, 6, 8} and
B = {2n : n ∈ N and n < 5}
When n = 1, 2n = 2 x 1= 2
When n = 2, 2n = 2 x 2= 4
When n = 3, 2n = 2 x 3= 6
When n = 4, 2n = 2 x 4= 8
∴ B = {2, 4, 6, 8}
Now we see that elements of sets A and B are the same (identical)
∴ Sets A and B are equal.
(ii)
M = {x : x ∈ W and x + 3 < 8}
x + 3 < 8
⇒ x < 8 – 3
⇒ x < 5
∴ M = {0, 1,2, 3, 4}
N = {y : y = 2n -1, n ∈ N and n < 5}
y = 2n – 1
When n = 1,
y = 2 x 1-1
⇒ y = 2-1
= 1
When n = 2,
y = 2 x 2-1
⇒ y = 4-1
= 3
When n =3,
y = 2 x 3-1
⇒ y = 6-1
= 5
When n = 4,
y = 2 x 4-1
⇒ y = 8-1
= 7
∴ N = {1, 3, 5,7}
Now we see that elements of sets M and N are not the same (identical)
∴ Sets M and N are not equal.
(iii)
E = {x : x2 + 8x – 9 = 0}
x2 + 8x – 9 = 0
⇒ x2 + 9x – x – 9 = 0
⇒ x(x+9) – 1(x+ 9) = 0
⇒ (x+1) (x+9) = 0
∴ Either x + 9 = 0
⇒ x = -9
Or
x – 1 = 0
⇒ x = 1
∴ E = {-9, 1}
F = {1, -9}
Now we see that the elements of sets E and F are the same (identical)
Sets E and F are equal.
(iv)
A = {x : x ∈ N, x < 3}
= {1, 2}
B = {y : y2 – 3y + 2 = 0}
y2 – 3y + 2 = 0
⇒ y2 – 2y – y + 2 = 0
⇒ y(y – 2) -1(y – 2) = 0
⇒ (y – 2)(y – 1) = 0
∴ Either y – 2 = 0
⇒ y = 2
Or
y – 1 = 0
⇒ y = 1
∴ B = {1, 2}
Now we see that elements of sets A and B are the same (identical).
∴ Sets A and B are equal.
Question 9 :-
State whether each of the following sets is a finite set or an infinite set:
(i) The set of multiples of 8.
(ii) The set of integers less than 10.
(iii) The set of whole numbers less than 12.
(iv) {x : x = 3n – 2, n ∈ W, n ≤ 8}
(v) {x : x = 3n – 2,n ∈ Z, n ≤ 8}
(vi) {x : x =n-2/n+2 , n ∈ w)
Answer :-
(i)
The set of multiples of 8.
= {8, 16, 24, 32, …..}
It is an infinite set.
(ii)
The set of integers less than 10.
= { 9, 8, 7, 6, 5, 4, 3, 2, 1, -1, -1, -2, …..}
It is an infinite set.
(iii)
The set of whole numbers less than 12
= {11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0}
It is a finite set.
(iv)
{x : x = 3n – 2, n ∈ W, n ≤ 8}
Substituting the value of n = (0, 1, 2, 3, 4, 5, 6, 7 and 8) we get
= {-2, 1, 4, 7, 10, 13, 16, 19, 22}
It is finite set.
(v)
{x : x = 3n – 2,n ∈ Z, n ≤ 8}
= {22, 19, 16, 13, 10, 7, 4, 1, -2, -5, ….}
It is infinite set.
(vi)
{x : x = n-2/n+2, n ∈ w)
{-2, -1/2,0,1/4,2/5…….}
It is infinite set.
Question 10 :-
Answer, whether the following statements are true or false. Give reasons.
(i) The set of even natural numbers less than 21 and the set of odd natural numbers less than 21 are equivalent sets.
(ii) If E = {factors of 16} and F = {factors of 20}, then E = F.
(iii) The set A = {integers less than 20} is a finite set.
(iv) If A = {x : x is an even prime number}, then set A is empty.
(v) The set of odd prime numbers is the empty set.
(vi) The set of squares of integers and the set of whole numbers are equal sets.
(vii) In n(P) = n(M), then P → M.
(viii) If set P = set M, then n(P) = n(M).
(ix) n(A) = n(B) ⇒ A = B.
Answer :-
(i)
True.
Reason:
Set of even natural number less than 21
= {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}
∴ Cardinal Number of this set = 10
Set of odd natural numbers less than 21
= {1, 3, 5, 7, 9, 11, 13, 15, 17, 19}
∴ Cardinal number of this set = 10
Now we see that cardinal number of both these sets = 10
∴ “The set of even natural numbers less than 21 and the set of odd natural numbers less than 21 are equivalent sets”. Hence it is a True statement.
(ii)
False.
Reason:
E = {Factors of 16}
= {1, 2, 4, 8, 16}
1 x 16 = 16
2 x 8 = 16
4 x 4 = 16
F = {Factors of 20}
= {1, 2, 4, 5, 10, 20}
1 x 20 = 20
2 x 10 = 20
4 x 5 = 20
Now we see that elements of set E and set F are not the same (identical)
∴ “if E = {Factors of 16} and F = {Factors of 20}, then E = F”……is a False statement.
(iii)
False.
Reason:
A = {Integers less than 20}
= {19, 18, 17, 16,…..,0, -1, -2, -3,….}
∴ “The set A = {Integers less than 20} is a finite set”……is a False statement.
(iv)
False.
Reason:
A = {x : x is an even prime number} = {2}
∴ “If A = {x : x is an even Prime number}, then set A is empty” ….. is a False statement.
(v)
False.
Reason:
Set of odd prime numbers
= {3, 5, 7, 11, 13, 17, 19, 23,….}
∴ “The set of odd prime numbers is the empty set” ……is a False statement.
(vi)
False.
Reason:
Integer Square of Integer Whole No.
0 : (0)2 = 0 0
±1 : (±1)2 = 1 1
±2 : (±2)2 = 4 2
±3 : (±3)2 = 9 3
±4 : (±4)2 = 16 4
±5 : (±5)2 = 25 5
….. : ….. ….. …..
….. : ….. ….. …..
∴ Set of square of integers
= {0, 1, 4, 9, 16, 25,…….}
Set of whole numbers = {0, 1, 2, 3, 4, 5, 6, 7,….}
Hence “The set of square of integers and the set of whole numbers are equal…False statement.
(vii)
True
Reason:
n(P) = n(M)
It means number of elements of set P
= Number of elements of set M.
∴ Sets P and M are equivalent.
∴ “If n(P) = n(M), then P ↔ M” … is a True statement.
(viii)
True.
Reason:
Set P = Set M
It means sets P and M are equal. Equal sets are equivalent also.
∴ Number of elements of set P = Number of elements of set M
∴ “If set P = set M, then n(P) = n(M)” ……..is a True statement.
(ix)
False
Reason:
n(A) = n(B)
⇒ Number of elements of set A
= Number of elements of set B
∴ Given sets are equivalent but not equal.
∴ “n(A) = n(B) ⇒ A = B” ……….is a False statement.
Exercise – 6 C Sets ICSE Class-8th Concise Selina Maths
Question 1 :-
Find all the subsets of each of the following sets :
(i) A = {5, 7}
(ii) B = {a, b, c}
(iii) C = {x : x ∈ W, x ≤ 2}
(iv) {p : p is a letter in the word ‘poor’}
Answer :-
(i)
A = {5,7}
Subsets of set A = { }, (5}, {7}, {5,7}
(ii)
B = {a, b, c}
Subsets of set B = { }, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}
(iii)
C = {x : x ∈ W, x ≤ 2}
= {0, 12}
∴ Subsets of set C = Φ, {0}, {1}, {2}, {0,1}, {0,2}, {1,2}, {0,1,2}
(iv)
{P : P is a letter in the word ‘POOR’}
= {p, o, o, r}
∴ Subsets of the given set = Φ, {p}, {o}, {r}, {p,o}, {p,r}, {p,r}, {o,r}, {p,o,r}
Question 2 :-
If C is the set of letters in the word “cooler”, find :
(i) Set C
(ii) n(C)
(iii) Number of its subsets
(iv) Number of its proper subsets.
Note : (i) If a set has n elements, the number of its subsets = 2n
(ii) If a set has n elements, the number of its proper subsets = 2n – 1
Answer :-
(i) C = {c, o, l, e, r}
(ii) n(C) = 5
(iii) Number of its subsets : 25 = 2 x 2 x 2 x 2 x 2 = 32
(iv) Number of its proper subsets = 25 – 1 = 32 – 1 = 31
Question 3 :-
If T = {x : x is a letter in the word ‘TEETH’}, find all its subsets.
Answer :-
T = {t,e,h}
Subsets of set T = φ, {r}, {e}, {h}, {t,e}, {t,h}, {e,h}, {t,e,h}
Question 4 :-
Given the universal set = {-7,-3, -1, 0, 5, 6, 8, 9}, find :
(i) A = {x : x < 2}
(ii) B = {x : -4 < x < 6}
Answer :-
(i)
Universal set = {-7, -3, -1, 0, 5, 6, 8, 9},
A = {x : x < 2} = {-7, -3, -1, 0}
(ii)
Universal set = {-7, -3, -1, 0, 5, 6, 8, 9},
B = {x : -4 < x < 6} = {-3, -1, 0, 5}
Question 5 :-
Given the universal set = {x : x ∈ N and x < 20}, find :
(i) A = {x : x = 3p ; p ∈ N}
(ii) B = {y : y – 2n + 3, n ∈ N}
(iii) C = {x : x is divisible by 4}
Answer :-
(i)
Universal set = {x : x ∈ N and x < 20}
= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11,….,19}
A = {x : x = 3p ; p ∈ N}
x = 3p
When p = 1,
x = 3 x 1
= 3
When p = 2,
x = 3 x 2
= 6
When p = 3,
x = 3 x 3
= 9
When p = 4,
x = 3 x 4
= 12
When p = 5,
x = 3 x 5
=15
When p = 6,
x = 3 x 6
= 18
∴ A = {3, 6, 9, 12, 15, 18}
(ii) B = {y : y – 2n + 3, n ∈ N}
y = 2n + 3
Question 6 :-
Find the proper subsets of {x : x2 – 9x – 10 = 0}
Answer :-
X2 – 9x – 10 = 0
⇒ x2 – 10x + x – 10 = 0
⇒ x(x-10)+1 (x-10) = 0
⇒ (x-10)(x+1) = 0
∴ Either x-10 = 0
⇒ x = 10
or
x+1 = 0
⇒ x = -1
Given set = {-1, 10}
Proper subsets of this set = φ, {-1}, {10}
Question 7 :-
Given, A = {Triangles}, B = {Isosceles triangles}, C = {Equilateral triangles}. State whether the following are true or false. Give reasons.
(i) A ⊆ B
(ii) B ⊆ A
(iii) C ⊆ B
(iv) B ⊂ A
(v) C ⊂ A
(vi) C ⊆ B ⊆ A
Answer :-
(i)
False.
Reason:
A = {Triangles}
B = {Isosceles triangles}
C = {Equilateral triangles}
Since each triangle is not isosceles.
∴ A ⊂ B
Hence, A ⊂ B is false.
(ii)
True
Reason:
A = {Triangles}
B = {Isosceles triangles}
C = {Equilateral triangle}
B ⊆ A … True
∵ Isosceles Δ is one of the triangles.
(iii)
True.
Reason:
A = {Triangles}
B = {Isosceles triangles}
C = {Equilateral triangle}
Since each equilateral triangle is isosceles also,
∴ C ⊆ B ….True
(iv)
True.
Reason:
A = {Triangle}
B = {Isosceles triangles}
C = {Equilateral triangles}
B ⊂ A ….True
∵ Isosceles Δ is one of the triangles.
(v)
True.
Reason:
A = {Triangles}
B = {Isosceles triangles}
C = {Equilateral triangles}
C ⊂ A ….True
∵ Equilateral Δ is one of the triangles.
(vi)
True.
Reason:
A = {Triangles}
B = {Isosceles triangles}
C = {Equilateral triangles}
C ⊆ B ⊆ A ….True
∵ Each equilateral triangle is isosceles also and each isosceles Δ is a form of triangles.
Question 8 :-
Given, A = {Quadrilaterals}, B = {Rectangles}, C = {Squares}, D= {Rhombuses}. State, giving reasons, whether the following are true or false.
(i) B ⊂ C
(ii) D ⊂ B
(iii) C ⊆ B ⊆ A
(iv) D ⊂ A
(v) B ⊇ C
(vi) A ⊇ B ⊇ D
Answer :-
(i)
False.
Reason:
A = {Quadrilaterals}
B = {Rectangles}
C = {Squares}
D= {Rhombuses}
B ⊂ C …..is a False.
∵ Rectangle is not a square also.
(ii)
False
Reason:
A = {Quadrilaterals}
B = {Rectangles}
C = {Squares}
D= {Rhombuses}
D ⊂ B ….. is a False.
∵ Rhombus is not a rectangle also.
(iii)
True
Reason:
A = {Quadrilaterals}
B = {Rectangles}
C = {Squares}
D= {Rhombuses}
C ⊆ B ⊆ A ….True
∵ Every square is a rectangle also and every rectangle is a quadrilateral also.
(iv)
True
Reason:
Given, A = {Quadrilaterals}
B = {Rectangles}
C = {Squares}
D= {Rhombuses}
D ⊂ A …..True
∵ Rhombus is one of the quadrilaterals.
(v)
True.
Reason:
A = {Quadrilaterals}
B = {Rectangles}
C = {Squares}
D = {Rhombuses}
B ⊇ C ….True
∵ Square is a rectangle also.
(vi)
False.
Reason:
A = {Quadrilaterals}
B = {Rectangles}
C = {Squares}
D= {Rhombuses}
A ⊇ B ⊇ D …..False
∵ Rhombus is not a rectangle also.
Question 9 :-

Answer :-
(i)
Universal set = {x : x ∈ N, 10 ≤ x ≤ 35}
= {10, 11, 12, 13, 14, 15,….,34, 35}
A = {x ∈ N : x ≤ 16}
= {{10, 11, 12, 13, 14, 15, 16}
A’ = {17, 18, 19, 20, 21, 22,…..,33, 34, 35}
= {x : x ∈ N ; 17 ≤ x ≤ 35}
(ii)
Universal set = {x : x ∈ N, 10 ≤ x ≤ 35}
= {10, 11, 12, 13, 14, 15,….,34, 35}
B = {x : x > 29}
= {30, 31, 32, 33, 34, 35}
B’ = {10, 11, 12, 13, 14, 15,…..,29}
= {x : x ≤ 29}
Question 10 :-
Given universal set = {x ∈ Z : -6 < x ≤6}.
N = {n : n is non-negative number}
(i) Find: N’
(ii) Find: P’
Answer :-
(i)
Universal set = {x ∈ Z ; -6 < x ≤ 6}
= {-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6}
N = {n : n is a non-negative number}
= {0, 1, 2, 3, 4, 5, 6}
N’ = {-5, -4, -3, -2, -1}
(ii)
Universal set = {x ∈ Z : -6 < x ≤ 6}
= {-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6}
P = {x : x is a non-positive number}
= (-5, -4, -3, -2, -1}
P’ = {1, 2, 3, 4, 5, 6}
Question 11 :-
Let M = {letters of the word REAL} and N = {letters of the word LARE}. Write sets M and N in roster form and then state whether;
(i) M ⊆ N is true.
(ii) N ⊆ M is true.
(iii) M = N is true.
Answer :-
(i)
M = {letters of the word REAL}
= {R, E, A, L}
and N = {letters of the word LARE}
= {L, A, R, E}
M ⊆ N is true : Yes
(ii)
M = {letters of the word REAL}
= {R, E, A, L}
and N = {letters of the word LARE}
= {L, A, R, E}
N ⊆ M is true : Yes
(iii)
M = {letters of the word REAL}
= {R, E, A, L}
and N = {letters of the word LARE}
= {L, A, R, E}
M = N is true : Yes
Question 12 :-
Write two sets A and B such that A ⊆ B and B ⊆ A.State the relationship between sets A and B.
Answer :-
Let A = {Letters of TALE}
B = {Letters of LATE}
Here A ⊆ B, and B ⊆ A
∴ A = B
Exercise – 6 D Solved Questions for ICSE 8th Set
Question 1 :-
Given A = {x : x ∈ N and 3 < x ≤ 6} and B = {x : x ∈ W and x < 4}.
(i) Find : Sets A and B in roster form.
(ii) Find: A ∪ B
(iii) Find: A ∩ B.
(iv) Find: A – B.
(v) Find: B – A.
Answer :-
(i) A = (4, 5, 6)
B = (0, 1 2, 3)
(ii) A ∪ B = {0, 1, 2, 3, 4, 5, 6}
(iii) A ∩ B = ( Φ )
(iv) A – B = (4, 5, 6)
(v) B – A = (0, 1, 2, 3)
Question 2 :-
If P = {x : x ∈ W and 4 ≤ x ≤ 8}, and Q = {x : x ∈ N and x < 6}.
(i) Find: P ∪ Q and P ∩ Q.
(ii) Find: Is (P ∪ Q) ⊃ (P ∩ Q)?
Answer :-
(i) P = (4, 5, 6, 7, 8)
Q = (1, 2, 3, 4, 5)
P ∪ Q = (1, 2, 3, 4, 5, 6, 7, 8)
P ∩ Q = (4, 5)
(ii) Yes, all the element of set P ∪ Q are contained in the set P ∩ Q.Therefore P ∪ Q is a proper subset of P ∪ Q.
Question 3 :-
If A = {5, 6, 7, 8, 9}, B = {x : 3 < x < 8 and x ∈ W} and C = {x : x ≤ 5 and x ∈ N}.
(i) A ∪ B and (A ∪ B) ∪ C
(ii) B ∪ C and A ∪ (B ∪ C)
(iii) A ∩ B and (A ∩ B) ∩ C
(iv)
B ∩ C and A ∩ (B ∩ C)
Is (A ∪ B) ∪ C = A ∪ (B ∪ C)?
Is (A ∩ B) ∩ C = A ∩ (B ∩ C)?
Answer :-
(i)
A = (5, 6, 7, 8, 9)
B = (4, 5. 6, 7)
C = (1, 2, 3, 4, 5)
A ∪ B = (4, 5, 6, 7, 8, 9)
(A ∪ B) ∪ C = (1, 2, 3, 4, 5, 6, 7, 8, 9)
(ii)
A = (5, 6, 7, 8, 9)
B = (4, 5. 6, 7)
C = (1, 2, 3, 4, 5)
B ∪ C = (1, 2, 3, 4, 5, 6, 7)
A ∪ (B ∪ C) = (1, 2 , 3, 4, 5, 6, 7, 8, 9)
(iii)
A = (5, 6, 7, 8, 9)
B = (4, 5. 6, 7)
C = (1, 2, 3, 4, 5)
A ∩ B = (5, 6, 7)
(A ∩ B) ∩ C = (5)
(iv)
A = (5, 6, 7, 8, 9)
B = (4, 5. 6, 7)
C = (1, 2, 3, 4, 5)
B ∩ C = (4, 5)
A ∩ (B ∩ C) = (5)
(A ∪ B) ∪ C = (1, 2, 3, 4, 5, 6, 7, 8, 9)
A ∪ (B ∪ C) = (1, 2, 3, 4, 5, 6, 7, 8, 9)
Yes, these are equal.
(A ∩ B) ∩ C = {5}
A ∩ (B ∩ C) = {5}
Yes, these are equal.
Question 4 :-
Given A = {0, 1, 2, 4, 5}, B = {0, 2, 4, 6, 8} and C = {0, 3, 6, 9}. Show that
(i) A ∪ (B ∪ C) = (A ∪ B) ∪ C i.e. the union of sets is associative.
(ii) A ∩ (B ∩ C) = (A ∩ B) ∩ C i.e. the intersection of sets is associative.
Answer :-
(i)
A = {0, 1, 2, 4, 5}
B = {0, 2, 4, 6, 8}
C = {0, 3, 6, 9}
B ∪ C = {0, 2, 4, 6, 8} ∪ {0, 3, 6, 9}
= {0, 2, 3, 4, 6, 8, 9}
∴ A ∪ (B ∪ C)
= {0, 1, 2, 4, 5} ∪ {0, 2, 3, 4, 6, 8, 9}
⇒ A ∪ (B ∪ C)
= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} ……(i)
A ∪ B = {0, 1, 2, 4, 5} ∪ {0, 2, 4, 6, 8}
= {0, 1, 2, 4, 5, 6, 8}
∴ (A ∪ B) ∪ C
= {0, 1, 2, 4, 5, 6, 7, 8} ∪ {0, 3, 6, 9}
⇒ (A ∪ B) ∪ C = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} …II
From I and II, we get
A ∪ (B ∪ C) = (A ∪ B) ∪ C
(ii)
B ∩ C = {0, 2, 4, 6, 8} ∩ {0, 3, 6, 9}
= {0,6}
Now, A ∩ (B ∩ C) = {0, 1, 2, 4, 5} ∩ {0,6}
⇒ A ∩ (B ∩ C) = {0} …(I)
A ∩ B = {0, 1, 2, 4, 5} ∩ {0, 2, 4, 6, 8}
= {0,2,4}
∴ (A ∩ B) ∩ C = {0,2,4} ∩ {0, 3, 6, 9}
⇒ (A ∩ B) ∩ C = {0} …(II)
From I and II we get
A ∩ (B ∩ C) = (A ∩ B) ∩ C
Question 5 :-
If A = {x ∈ W : 5 < x < 10}, B = {3, 4, 5, 6, 7} and C = {x = 2n; n ∈ N and n ≤4}. Find:
(i) A ∩ (B ∪ C)
(ii) (B ∪ A) ∩ (B ∪ C)
(iii) B ∪ (A ∩ C)
(iv) (A ∩ B) ∪ (A ∩ C)
Answer :-
(i)
A = {x ∈ W : 5 < x < 10}
= {6, 7, 8, 9}
B = {3, 4, 5, 6, 7}
C = {x = 2n; n ∈ N and n ≤4}
x = 2n
When n = 1,
x = 2 x 1
= 2
When n = 2,
x = 2 x 2
= 4
When n = 3,
x = 2 x 3
= 6
When n =4,
x = 2 x 4
= 8
∴ C = {2, 4, 6, 8}
B ∪ C
= {3, 4, 5, 6, 7} ∪ {2, 4. 6, 8}
= {2, 3, 4, 5, 6, 7, 8}
A ∩ (B ∪ C)
= {6. 7, 8, 9} ∩ {2, 3, 4, 5, 6, 7, 8}
⇒ A ∩ (B ∪ C) = {6, 7, 8}
(ii)
A = {x ∈ W : 5 < x < 10}
= {6, 7, 8, 9}
B = {3, 4, 5, 6, 7}
C = {x = 2n; n ∈ N and n ≤4}
x = 2n
When n = 1,
x = 2 x 1
= 2
When n = 2,
x = 2 x 2
= 4
When n = 3,
x = 2 x 3
= 6
When n =4,
x = 2 x 4
= 8
∴ C = {2, 4, 6, 8}
B ∪ A
= {3, 4, 5, 6, 7} ∪ {6, 7, 8, 9}
= {3, 4, 5, 6, 7, 8, 9}
(B ∪ A) ∩ (B ∪ C)
= {3, 4, 5, 6, 7, 8, 9} ∩ {2, 3, 4, 5, 6, 7, 8}
= {3, 4, 5, 6, 7, 8}
(iii)
A = {x ∈ W : 5 < x < 10}
= {6, 7, 8, 9}
B = {3, 4, 5, 6, 7}
C = {x = 2n; n ∈ N and n ≤4}
x = 2n
When n = 1,
x = 2 x 1
= 2
When n = 2,
x = 2 x 2
= 4
When n = 3,
x = 2 x 3
= 6
When n =4,
x = 2 x 4
= 8
∴ C = {2, 4, 6, 8}
(A ∩ C)
= {6, 7, 8, 9} ∩ {2, 4, 6. 8}
= {6, 8}
B ∪ (A ∩ C)
= {3, 4, 5, 6, 7} ∪ {6, 8}
= {3, 4, 5, 6, 7, 8}
(iv)
A = {x ∈ W : 5 < x < 10}
= {6, 7, 8, 9}
B = {3, 4, 5, 6, 7}
C = {x = 2n; n ∈ N and n ≤4}
x = 2n
When n = 1,
x = 2 x 1
= 2
When n = 2,
x = 2 x 2
= 4
When n = 3,
x = 2 x 3
= 6
When n =4,
x = 2 x 4
= 8
∴ C = {2, 4, 6, 8}
(A ∩ B)
= {6, 7, 8, 9} ∩ {3, 4, 5, 6, 7}
= {6, 7}
∴ (A ∩ B) ∪ (A ∩ C)
= {6, 7} ∪ {6, 8}
= {6, 7, 8}
Question 6 :-
If P = {factors of 36} and Q = {factors of 48}; Find:
(i) P ∪ Q
(ii) P ∩ Q
(iii) Q – P.
(iv) P’ ∩ Q.
Answer :-
(i)
1 x 36 = 36
2 x 18 = 36
3 x 12 = 36
4 x 9 = 36
6 x 6 = 36
1 x 48 = 48
2 x 24 = 48
3 x 16 = 48
4 x 12 = 48
6 x 8 = 48
∴ Factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18, 36
Factors of 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
P = {Factors of 36}
= {1, 2, 3, 4, 6, 8, 12, 18, 36}
Q = {Factors of 48}
= {1, 2, 3, 4, 6, 8, 12, 16, 24, 48}
P ∪ Q = {1, 2, 3, 4, 6, 9, 12, 18, 36} ∪ {1, 2, 3, 4, 6, 8, 12, 16, 24, 48}
= {1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 36, 48}
(ii)
1 x 36 = 36
2 x 18 = 36
3 x 12 = 36
4 x 9 = 36
6 x 6 = 36
1 x 48 = 48
2 x 24 = 48
3 x 16 = 48
4 x 12 = 48
6 x 8 = 48
∴ Factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18, 36
Factors of 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
P = {factors of 36}
= {1, 2, 3, 4, 6, 8, 12, 18, 36}
Q = {factors of 48}
= {1, 2, 3, 4, 6, 8, 12, 16, 24, 48}
P ∩ Q = {1, 2, 3, 4, 6, 9, 12, 18, 36} ∩ {1, 2, 3, 4, 6, 8, 12, 16, 24, 48}
={1, 2, 3, 4, 6, 12}
(iii)
1 x 36 = 36
2 x 18 = 36
3 x 12 = 36
4 x 9 = 36
6 x 6 = 36
1 x 48 = 48
2 x 24 = 48
3 x 16 = 48
4 x 12 = 48
6 x 8 = 48
∴ Factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18, 36
Factors of 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
P = {factors of 36}
= {1, 2, 3, 4, 6, 8, 12, 18, 36}
Q = {factors of 48}
= {1, 2, 3, 4, 6, 8, 12, 16, 24, 48}
Q – P = {1, 2, 3, 4, 6, 8, 12, 16, 24, 48} – {1, 2, 3, 4, 6, 9, 12, 18, 36}
= {8, 16, 24, 48}
(iv)
1 x 36 = 36
2 x 18 = 36
3 x 12 = 36
4 x 9 = 36
6 x 6 = 36
1 x 48 = 48
2 x 24 = 48
3 x 16 = 48
4 x 12 = 48
6 x 8 = 48
∴ Factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18, 36
Factors of 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
P = {factors of 36}
= {1, 2, 3, 4, 6, 8, 12, 18, 36}
Q = {factors of 48}
= {1, 2, 3, 4, 6, 8, 12, 16, 24, 48}
P’ ∩ Q = Only Q
= Q – P
= {1, 2, 3, 4, 6, 8, 12, 16, 24, 48} – {1, 2, 3, 4, 6, 9, 12, 18, 36}
= {8, 16, 24, 48}
Question 7. :-
If A = {6, 7, 8, 9}, B = {4, 6, 8,10} and C = {x : x ∈ N : 2 < x ≤ 7}; Find:
(i) A -B.
(ii) B – C
(iii) B – (A – C).
(iv) A – (B ∪ C).
(v) B – (A ∩ C).
(vi) B – B.
Answer :-
(i) A -B.
A = {6, 7, 8, 9}
B = {4, 6, 8, 10}
C = {x : x ∈ N : 2 < x ≤ 7}
= {3, 4, 5, 6, 7}
A – B = {6, 7, 8, 9} – {4, 6, 8, 10}
= {7, 9}
(ii) B – C
A = {6, 7, 8, 9}
B = {4, 6, 8, 10}
C = {x : x ∈ N : 2 < x ≤ 7}
= {3, 4, 5, 6, 7}
B – C = {4, 6, 8, 10} – {3, 4, 5, 6, 7}
= {8, 10}
(iii) B – (A – C).
A = {6, 7, 8, 9}
B = {4, 6, 8, 10}
C = {x : x ∈ N : 2 < x ≤ 7}
= {3, 4, 5, 6, 7}
A – C = {6, 7, 8, 9} – {3, 4, 5, 6, 7}
= {8, 9}
B – (A – C) = {4, 6, 8, 10} – {8, 9}
= {4, 6, 10}
(iv) A – (B ∪ C).
(B ∪ C) = {4, 6, 8, 10} ∪ {3, 4, 5, 6, 7}
= {3, 4, 5, 6, 7, 8,10}
A – (B ∪ C) = {6, 7, 8, 9} – {3, 4, 5, 6, 7, 8, 10}
= {9}
(v) B – (A ∩ C).
A = {6, 7, 8, 9}
B = {4, 6, 8, 10}
C = {x : x ∈ N : 2 < x ≤ 7}
= {3, 4, 5, 6, 7}
A ∩ C = {6, 7, 8, 9} ∩ {3, 4, 5, 6, 7}
= {6, 7}
B – (A ∩ C) = {4, 6, 8, 10} – {6,7}
= {4, 8,10}
(vi) B – B.
A = {6, 7, 8, 9}
B = {4, 6, 8, 10}
C = {x : x ∈ N : 2 < x ≤ 7}
= {3, 4, 5, 6, 7}
B – B = {4, 6, 8, 10} – {4, 6, 8, 10}
= Φ
Question 8 :-
If A = {1, 2, 3, 4, 5}
B = {2, 4, 6, 8}
and C = {3, 4, 5, 6}
(i) Verify : A – (B ∪ C) = (A – B) ∩ (A – C)
Answer :-
(i)
A = {1, 2, 3, 4, 5}
B = {2, 4, 6, 8}
C = {3, 4, 5, 6}
B ∪ C = {2, 4, 6, 8} ∪ {3, 4, 5, 6}
= {2, 3, 4, 5, 6, 8}
A – (B ∪ C) = {1, 2, 3, 4, 5} – {2, 3, 4, 5, 6, 8}
= {1}
A – B = {1, 2, 3, 4, 5} – {2, 4, 6, 8}
= {1, 3, 5}
A – C = {1, 2, 3, 4, 5} – {3, 4, 6, 8}
= {1,2}
∴ (A – B) ∩ (A – C) = {1, 3, 5} – {1,2}
= {1}
∴ A – (B ∪ C) = (A – B) ∩ (A – C)
(ii)
A = {1, 2, 3, 4, 5}
B = {2, 4, 6, 8}
C = {3, 4, 5, 6}
B ∩ C = {2, 4, 6, 8} ∩ {3, 4, 5, 6}
= {4,6}
A – (B ∩ C) = {1, 2, 3, 4, 5} – {4,6}
= {1, 2, 3, 5}
A – B = {1, 2, 3, 4, 5} – {2, 4, 6, 8}
= {1, 3, 5}
A -C = {1, 2, 3, 4, 5} – {3, 4, 5, 6}
= {1,2}
(A – B) ∪ (A – C) = {1, 3, 5} ∪ {1,2}
= {1, 2, 3, 5}
∴ A – (B ∩ C) = (A – B) ∪ (A – C)
Question 9 :-
Given A = {x : ∈ N :< 6}, B = {3, 6, 9} and C = {x ∈ N : 2x – 5 ≤ 8}. show that:
(i) A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
(ii) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
Answer :-
(i)
A = {x : ∈ N :< 6}
B = {3, 6, 9}
C = {x ∈ N : 2x – 5 ≤ 8}
2x – 5 ≤ 8
⇒ 2x ≤ 8+5
⇒ 2x ≤ 13
⇒ x ≤ 13/2
⇒ x ≤ 6.5
∴ C = {1, 2, 3, 4, 5, 6}
B ∩ C = {3, 6, 9} ∩ {1, 2, 3, 4, 5, 6}
= {3,6}
∴ A ∪ (B ∩ C) = {1, 2, 3, 4, 5} ∪ {3,6}
= {1, 2, 3, 4, 5, 6}
A ∪ B = {1, 2, 3, 4, 5} ∪ {3, 6, 9}
= {1, 2, 3, 4, 5, 6, 9}
A ∪ C = {1, 2, 3, 4, 5} ∪ {1, 2, 3, 4, 5, 6}
= {1, 2, 3, 4, 5, 6}
∴ (A ∪ B) ∩ (A ∪ C)
= {1, 2, 3, 4, 5, 6, 9} ∩ {1, 2, 3, 4, 5, 6}
= {1, 2, 3, 4, 5, 6}
∴ A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
(ii)
A = {x : ∈ N :< 6}
B = {3, 6, 9}
C = {x ∈ N : 2x – 5 ≤ 8}
2x – 5 ≤ 8
⇒ 2x ≤ 8+5
⇒ 2x ≤ 13
⇒ x ≤ 13/2
⇒ x ≤ 6.5
∴ C = {1, 2, 3, 4, 5, 6}
B ∪ C = {3, 6, 9} ∪ {1, 2, 3, 4, 5, 6}
= {1, 2, 3, 4, 5, 6, 9}
A ∩ (B ∪ C) = {1, 2, 3, 4, 5} ∩ {1, 2, 3, 4, 5, 6, 9}
= {1, 2, 3, 4, 5}
Now A ∩ C = {1, 2, 3, 4, 5} ∩ {1, 2, 3, 4, 5, 6}
= {1, 2, 3, 4, 5}
A ∩ B = {1, 2, 3, 4, 5} ∩ {3, 6, 9}
= {3}
∴ (A ∩ B) ∪ (A ∩ C) = {3} ∪ {1, 2, 3, 4, 5}
= {1, 2, 3, 4, 5}
∴ A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
Exercise – 6 E Sets ICSE Class-8th Selina Solutions
Question 1 :-

Answer :-
(i) A ∪ B = {a, c, d, e} ∪ {b, c, e, f}
⇒ A ∪ B = {a, b, c, d, e, f}
(ii) A’ = {b ,f, g, h}
A’ ∩ B = {b, f, g, h} ∩ {b, c, e, f}
⇒ A’ ∩ B = {b, f}
(iii) A – B = {a, c, d, e} – {b, c, e, f}
⇒ A – B = {a, d}
(iv) B – A = {b, c, e, f} – {a, c, d, e}
= {b, f}
(v) A ∪ B = {a, b, c, d, e, f}
∴ (A ∪ B)’ = {h, g}
Question 2 :-
From the given diagram, find :
(i) A’
(ii) B’

Answer :-
(i) A = {1, 3, 4, 6}
A’ = {2, 5, 7, 8, 9, 10}
(ii) B = {1, 2, 5}
∴ B’ = {3, 4, 6, 7, 8, 9, 10}
(iii) A’ ∪ B’ = {2, 5, 7, 8, 9, 10} ∪ {3, 4, 6, 7, 8, 9, 10}
= {2, 3, 4, 5, 6, 7, 8, 9, 10}
(iv) A ∩ B = {1, 3, 4, 6} ∩ {1, 2, 5}
= {1}
∴ (A ∩ B)’ = {2, 3, 4, 5, 6, 7, 8, 9, 10}
From Part (iii) and Part (iv) we conclude
A’ ∪ B’ = (A ∩ B)’
Now A ∩ B = {2, 5, 7, 8, 9, 10} ∩ {3, 4, 6, 7, 8, 9, 10}
⇒ A’ ∪ B’ = {7, 8, 9, 10} …(I)
Now A ∪ B = {1, 3, 4, 6} ∪ {1, 2, 5}
= {1, 2, 3, 4, 5, 6}
∴ (A ∩ B)’ = {7, 8, 9, 10} …(II)
From I and II we conclude
A’ ∪ B’ = (A ∩ B)’
Question 3 :-

Answer :-
(i) B ∩ C = {d, e, f, g, h} ∩ {h, i, k, l}
= {h, j}
∴ A ∪ (B ∩ C) = {a, b, c, d, g, h, i, j} ∪ {h, j}
= {a, b, c, d, g, h, i, j}
(ii) A – C = {a, b, c, d, g, h, i} – {h, i, j, k, l}
= {a, b, c, d, g}
∴ B – (A – C) = {d, e, f, g, h, j} – {a, b, c, d, g}
= {e, f, h, j}
(iii) A – B = {a, b, c, d, g, h, i} – {d, e, f, g ,h, i}
⇒ A – B = {a, b, c, i} …(I)
(iv) B’ = {a, b, c ,i, k, l, m, n, p}
A ∩ B’ = {a, b, c, d, g, h, i} ∩ {a, b, c, i, k, l, m, n, p}
⇒ A ∩ B’ = {a, b, i} …(II)
From I and II we can conclude A ∩ B’ = A – B
Question 4 :-

Answer :-
(i) B – A = {1, 5} – {1, 5, 6, 7, 9}
= { }
(ii) A = {1, 5, 6, 7, 9}
(iii) B = {1, 5}
∴ B’ = {2, 3, 4, 6, 7, 8, 9, 10}
(iv) A ∩ B = {1, 5, 6, 7, 9} ∩ {1,5}
= {1,5}
(v) A ∪ B = {1, 5, 6, 7, 9} ∪ {1,5}
= {1,5, 6, 7, 9}
Question 5 :-
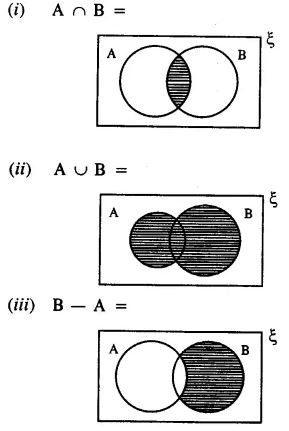
Draw a Venn-diagram to show the relationship between two overlapping sets A and B. Now shade the region representing :
(i) A ∩ B
(ii) A ∪ B
(iii) B – A
Answer :-
(i) A ∩ B
Question 6 :-

Answer :-
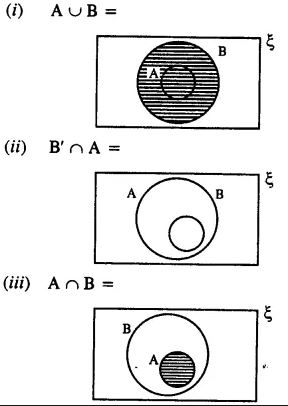
(iv) 
Question 7 :-

Answer :-
Try yourself !
Question 8 :-


Answer :-
(i) (A ∪ B)’
(ii) B – A or A’ ∩ B
(iii) (B – A)’
Question 9 :-

Answer :-
Try yourself !
Question 10 :-

Answer :-
(i) A ∪ B = {a, b, c, d} ∪ {c, d, e, g}
= {a, b, c, d, e, g}
∴ (A ∪ B) – C = {a, b, c, d, e, g} – {b, c, e, f}
= {a, d, g}
(ii) (A ∩ C) = {a, b, c, d} ∩ {b, c, e, f}
= {b, c}
∴ B – (A ∩ C) = {c, d, e, g} – {b, c}
= {d, e, g}
(iii) B ∩ C = {c, e, d, g} ∩ {b, c, e, f}
= {c, e}
∴ A – (B ∩ C) = (A – B) ∪ (A – C)
⇒ (B ∩ C) = {c, e}
So, A − (B ∩ C) = {a, b, d} …..(1)
Question 11 :-

:
Answer :-
(i)
{a, d} = {a, b, e, d} – {b, c, e, f}
= A – B
(ii)
{a, d, c, f} = {A ∪ B) – {b, e}
= {A ∪ B) – (A ∩ B)
Also {a, d, c, f} = (A – B) ∪ (B – A)
(iii)
{a, d, c, f, g, h} = (A ∩ B)’
[∵ {b, e} = A ∩ B ∴ (A ∩ B)’ = {a, d, c, f, g, h}]
(iv)
{a, d, g, h} = B’
[∵ {b, c, e, f} = B ∴ B’ = {a, d, g, h}]
(v)
{g, h} = (A ∪ B)’
[∵ A ∪ B = {a, b, c, d, e, f} ∴ (A ∪ B)’ = {g, h}]
— End of Sets Solutions :–
Return to – Concise Selina Maths Solutions for ICSE Class -8
Thanks



If a (1,2,3,4,5,6,7,8,9,10) find
now full chapter PDF showing/ working
please visit again for analysis