ML Aggarwal Similarity Exe-13.1 Class 10 ICSE Maths Solutions

ML Aggarwal Similarity Exe-13.1 Class 10 ICSE Maths Solutions. We Provide Step by Step Answer of Exe-13.1 Questions for Similarity as council prescribe guideline for upcoming board exam. Visit official Website  CISCE  for detail information about ICSE Board Class-10.

ML Aggarwal Similarity Exe-13.1 Class 10 ICSE Maths Solutions

Board	ICSE
Subject	Maths
Class	10th
Chapter-13	Similarity
Writer / Book	Understanding
Topics	Solutions of Exe-13.1
Academic Session	2024-2025

Similarity Exe-13.1 Questions

ML Aggarwal Class 10 ICSE Maths Solutions

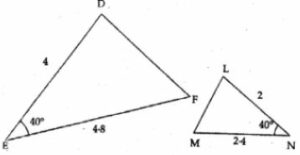
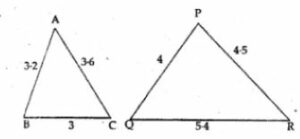
Question 1. State which pairs of triangles in the figure given below are similar. Write the similarity rule used and also write the pairs of similar triangles in symbolic form (all lengths of sides are in cm):

Answer :

Given

(i) In ∆ABC and PQR

AB/PQ = 3.2/4 = 4/5

AC/PR = (3.6/4.5) = 4/5

BC/QR = 3/5.4 = 5/9

(ii) In ∆DEF and ∆LMN

∠E = ∠N = 40°

DE/LN = 4/2 = 2/1 and

EF/MN = 4.8/2.4

= 2/1

∴ ∆DEF ~ ∆LMN (SAS axiom)

Question 2. If in two right triangles, one of the acute angle of one triangle is equal to an acute angle of the other triangle, can you say that the two triangles are similar? Why?

Answer :

In two right triangles,
one of the acute angles of the one triangle is
equal to an acute angle of the other triangle.
The triangles are similar. (AAA axiom)

Question 3. It is given that ∆ABC ~ ∆EDF such that AB = 5 cm, AC = 7 cm, DF = 15 cm and DE = 12 cm.
Find the lengths of the remaining sides of the triangles.

Answer :

∆ABC ~ ∆EDF
AB = 5 cm, AC = 7 cm, DF = 15 cm and DE = 12 cm

ΔDEF ~ ΔLMN

So, AB/ED = AC/EF = BC/DF

Consider AB/ED = AC/EF

5/12 = 7/EF

By cross multiplication,

EF = (7 × 12)/5

EF = 16.8 cm

Now, consider AB/ED = BC/DF

5/12 = BC/15

BC = (5 × 15)/12

BC = 75/12

BC = 6.25

Question 4.

(a) If ∆ABC ~ ∆DEF, AB = 4 cm, DE = 6 cm, EF = 9 cm and FD = 12 cm, then find the perimeter of ∆ABC.
(b) If ∆ABC ~ ∆PQR, Perimeter of ∆ABC = 32 cm, perimeter of ∆PQR = 48 cm and PR = 6 cm, then find the length of AC.

Answer :

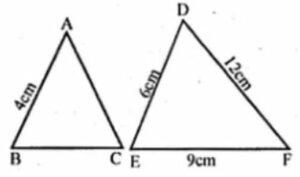
(a) ∆ABC ~ ∆DEF
AB = 4 cm, DE = 6 cm, EF = 9 cm and FD = 12 cm

Let ΔABC ~ ΔDEF

So, AB/DE = AC/DF = BC/EF

Consider, AB/DE = AC/DE

4/6 = AC/12

By cross multiplication we get,

AC = (4 × 12)/6

AC = 48/6

AC = 8 cm

Then, consider AB/DE = BC/EF

4/6 = BC/9

BC = (4 × 9)/6

BC = 36/6

BC = 6 cm

Therefore, the perimeter of ΔABC = AB + BC + AC

= 4 + 6 + 8

= 18 cm

(b)

∆ABC ~ ∆PQR

Perimeter of ∆ABC = 32 cm

Perimeter of ∆PQR = 48 cm

So, AB/PQ = AC/PR = BC/QR

Then, perimeter of ∆ABC/perimeter of ∆PQR = AC/PR

32/48 = AC/6

AC = (32 × 6)/48

AC = 4

Therefore, the length of AC = 4 cm.

Question 5. Calculate the other sides of a triangle whose shortest side is 6 cm and which is similar to a triangle whose sides are 4 cm, 7 cm and 8 cm.

Answer :

Let ∆ABG ~ ∆DEF in which shortest side of
∆ABC is BC = 6 cm.
In ∆DEF, DE = 8 cm, EF = 4 cm and DF = 7 cm

∆ABC is BC = 6cm

∆ABC ~ ∆DEF

So, AB/DE = BC/EF = AC/DF

Consider AB/DE = BC/EF

AB/8 = 6/4

AB = (6 × 8)/4

AB = 48/4

AB = 12

Now, consider BC/EF = AC/DF

6/4 = AC/7

AC = (6 × 7)/4

AC = 42/4

AC = 21/2

AC = 10.5 cm

Question 6.

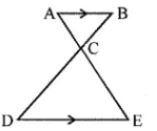
(a) In the figure given below, AB || DE, AC = , 3 cm, CE = 7.5 cm and BD = 14 cm. Calculate CB and DC.

(b) In the figure (2) given below, CA || BD, the lines AB and CD meet at G.
(i) Prove that ∆ACO ~ ∆BDO.
(ii) If BD = 2.4 cm, OD = 4 cm, OB = 3.2 cm and AC = 3.6 cm, calculate OA and OC.

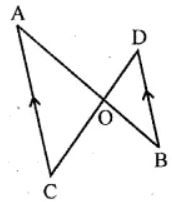
Answer :

(a) In the given figure,

AB||DE, AC = 3 cm, CE = 7.5 cm, BD = 14 cm

From the question it is given that,

AB||DE

AC = 3 cm

CE = 7.5 cm

BD = 14 cm

From the figure,

∠ACB = ∠DCE [because vertically opposite angles]

∠BAC = ∠CED [alternate angles]

Then, ∆ABC ~ ∆CDE

So, AC/CE = BC/CD

3/7.5 = BC/CD

By cross multiplication we get,

7.5BC = 3CD

Let us assume BC = x and CD = 14 – x

7.5 × x = 3 × (14 – x)

7.5x = 42 – 3x

7.5x + 3x = 42

10.5x = 42

x = 42/10.5

x = 4

Therefore, BC = x = 4 cm

CD = 14 – x

= 14 – 4

= 10 cm

(i) We have to prove that, ∆ACO ~ ∆BDO.

So, from the figure

Consider ∆ACO and ∆BDO

Then,

∠AOC = ∠BOD [from vertically opposite angles]

∠A = ∠B

Therefore, ∆ACO = ∆BDO

Given, BD = 2.4 cm, OD = 4 cm, OB = 3.2 cm, AC = 3.6 cm,

∆ACO ~ ∆BOD

So, AO/OB = CO/OD = AC/BD

Consider AC/BD = AO/OB

3.6/2.4 = AO/3.2

AO = (3.6 × 3.2)/2.4

AO = 4.8 cm

Now, consider AC/BD = CO/OD

3.6/2.4 = CO/4

CO = (3.6 × 4)/2.4

CO = 6 cm

Question 7.

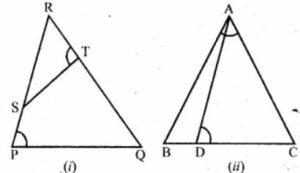
(a) In the figure

(i) given below, ∠P = ∠RTS.
Prove that ∆RPQ ~ ∆RTS.

(b) In the figure

(ii) given below,

∠ADC = ∠BAC. Prove that CA² = DC x BC.

Answer :

(a) In the given figure, ∠P = ∠RTS

To prove : ∆RPQ ~ ∆RTS
Proof : In ∆RPQ and ∆RTS
∠R = ∠R (common)
∠P = ∠RTS (given)
∆RPQ ~ ∆RTS (AA axiom)

(b)

From the figure, ∠ADC = ∠BAC

So, we have to prove that, CA² = DC x BC

In ∆ABC and ∆ADC

∠C = ∠C (common angle for both triangle)

∠BAC = ∠ADC (from the question)

∆ABC ~ ∆ADC

Therefore, CA/DC = BC/CA

We know that, corresponding sides are proportional,

Therefore, CA² = DC × BC

Question 8.

(a) In the figure (1) given below, AP = 2PB and CP = 2PD.

(i) Prove that ∆ACP is similar to ∆BDP and AC || BD.
(ii) If AC = 4.5 cm, calculate the length of BD.

(b) In the figure (2) given below,

∠ADE = ∠ACB.

(i) Prove that ∆s ABC and AED are similar.
(ii) If AE = 3 cm, BD = 1 cm and AB = 6 cm, calculate AC.

(c) In the figure (3) given below, ∠PQR = ∠PRS. Prove that triangles PQR and PRS are similar. If PR = 8 cm, PS = 4 cm, calculate PQ.

figure see in your textbook

Answer :

In the given figure,
AP = 2PB, CP = 2PD
To prove:

(a) From the question it is give that,

AP = 2PB, CP = 2PD

(i) We have to prove that, ∆ACP is similar to ∆BDP and AC || BD

AP = 2PB

AP/PB = 2/1

Then, CP = 2PD

CP/PD = 2/1

∠APC = ∠BPD [from vertically opposite angles]

So, ∆ACP ~ ∆BDP

Therefore, ∠CAP = ∠PBD [alternate angles]

Hence, AC || BD

(ii) AP/PB = AC/BD = 2/1

AC = 2BD

2BD = 4.5 cm

BD = 4.5/2

BD = 2.25 cm

(b)

From the given figure,

(i) ∠A = ∠A (common angle for both triangles)

∠ACB = ∠ADE [given]

Therefore, ∆ABC ~ ∆AED

(ii) from (i) proved that, ∆ABC ~ ∆AED

So, BC/DE = AB/AE = AC/AD

AD = AB – BD

= 6 – 1 = 5

Consider, AB/AE = AC/AD

6/3 = AC/5

AC = (6 × 5)/3

AC = 30/3

AC = 10 cm

(c)

∠P = ∠P (common angle for both triangles)

∠PQR = ∠PRS [from the question]

So, ∆PQR ~ ∆PRS

Then, PQ/PR = PR/PS = QR/SR

Consider PQ/PR = PR/PS

PQ/8 = 8/4

PQ = (8 × 8)/4

PQ = 64/4

PQ = 16 cm

---

Similarity Exe-13.1 Questions

ML Aggarwal Class 10 ICSE Maths Solutions

Page-263

Question 9. In the given figure, ABC is a triangle in which AB = AC. P is a point on the side BC such that PM ⊥ AB and PN ⊥ AC. Prove that BM x NP = CN x MP.

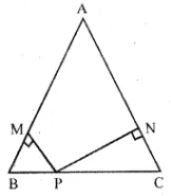
Answer :

In the given figure, ABC in which AB = AC.
P is a point on BC such that PM ⊥ AB and PN ⊥ AC
To prove : BM x NP = CN x MP

Consider the ∆ABC

AB = AC … [from the question]

∠B = ∠C … [angles opposite to equal sides]

Then, consider ∆BMP and ∆CNP

∠M = ∠N

Therefore, ∆BMP ~ ∆CNP

So, BM/CN = MP/NP

By cross multiplication we get,

BM x NP = CN x MP

Hence it is proved.

Question 10. Prove that the ratio of the perimeters of two similar triangles is the same as the ratio of their corresponding sides.

Answer :

Given : ∆ABC ~ ∆PQR .
To prove : Ratio in their perimeters k
the same as the ratio in their corresponding sides.

From the question it is given that, two triangles are similar triangles

So, ∆MNO ~ ∆XYZ

If two triangles are similar, the corresponding angles are equal and their corresponding sides are proportional.

MN/XY = NO/YZ = MO/XZ

Perimeter of ∆MNO = MN + NO + MO

Perimeter of ∆XYZ = XY + YZ + XZ

Therefore, (MN/XY = NO/YZ = MO/XZ) = (MN/XY + NO/YZ + MO/XZ)

= Perimeter of ∆MNO/perimeter of ∆XYZ

Question 11. In the adjoining figure, ABCD is a trapezium in which AB || DC. The diagonals AC and BD intersect at O. Prove that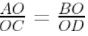

Using the above result, find the value(s) of x if OA = 3x – 19, OB = x – 4, OC = x – 3 and OD = 4.

Answer :

ABCD is a trapezium in which AB || DC
Diagonals AC and BD intersect each other at O.

we have to prove that, AO/OC = BO/OD

Consider the ∆AOB and ∆COD,

∠AOB = ∠COD … [vertically opposite angles]

∠OAB = ∠OCD

Hence, ∆AOB ~ ∆COD

So, OA/OC = OB/OD

Now by using above result we have to find the value of x if OA = 3x – 19, OB = x – 4, OC = x – 3 and OD = 4.

OA/OC = OB/OD

(3x – 19)/(x – 3) = (x – 4)/4

By cross multiplication we get,

(x – 3) (x – 4) = 4(3x – 19)

X² – 4x – 3x + 12 = 12x – 76

X² – 7x + 12 – 12x + 76 = 0

X² – 19x + 88 = 0

X² – 8x – 11x + 88 = 0

X(x – 8) – 11(x – 8) = 0

(x – 8) (x – 11) = 0

Take x – 8 = 0

X = 8

Then, x – 11= 0

X = 11

Hence, the value of x is 8 and 11.

Question 12.

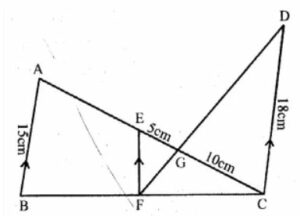
(a) In the figure given below, AB, EF and CD are parallel lines. Given that AB =15 cm, EG = 5 cm, GC = 10 cm and DC = 18 cm. Calculate

(i) EF
(ii) AC.

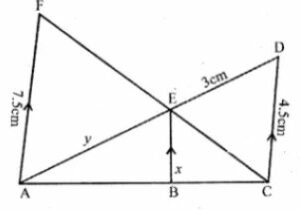
(b) In the figure given below, AF, BE and CD are parallel lines. Given that AF = 7.5 cm, CD = 4.5 cm, ED = 3 cm, BE = x and AE = y. Find the values of x and y.

Answer :

(a) In the given figure,
AB || EF || CD
AB = 15 cm, EG = 5 cm, GC = 10 cm and DC = 18 cm
Calculate :

(i) Consider the ∆EFG and ∆CGD

∠EGF = ∠CGD [Because vertically opposite angles are equal]

∠FEG = ∠GCD [alternate angles are equal]

Therefore, ∆EFG ~ ∆CGD

Then, EG/GC = EF/CD

5/10 = EF/18

EF = (5 × 18)/10

Therefore, EF = 9 cm

(ii) Now, consider the ∆ABC and ∆EFC

EF ||AB

So, ∆ABC ~ ∆EFC

Then, AC/EC = AB/EF

AC/(5 + 10) = 15/9

AC/15 = 15/9

AC = (15 × 15)/9

Hence, AC = 25 cm

(b)

Consider the ∆AEF and ∆CED

∠AEF and ∠CED [because vertically opposite angles are equal]

∠F = ∠C [alternate angles are equal]

Therefore, ∆AEF ~ ∆CED

So, AF/CD = AE/ED

7.5/4.5 = y/3

By cross multiplication,

y = (7.5 × 3)/4.5

y = 5 cm

So, similarly in ∆ACD, BE ||CD

Therefore, ∆ABE ~ ∆ACD

EB/CD = AE/AD

x/CD = y/y + 3

x/4.5 = 5/(5 + 3)

x/4.5 = 5/8

x = (4.5 × 5)/8

x = 22.5/8

x = 225/80

x = 45/16

x = 2(13/16)

---

Similarity Exe-13.1 Questions

ML Aggarwal Class 10 ICSE Maths Solutions

Page-264

Question 13. In the given figure, ∠A = 90° and AD ⊥ BC If BD = 2 cm and CD = 8 cm, find AD.

Answer :

So, ∠A = 90^o

And AD ⊥ BC

∠BAC = 90^o

Then, ∠BAD + ∠DAC = 90^o … [equation (i)]

Now, consider ∆ADC

∠ADC = 90^o

So, ∠DCA + ∠DAC = 90^o … [equation (ii)]

From equation (i) and equation (ii)

We have,

∠BAD + ∠DAC = ∠DCA + ∠DAC

∠BAD = ∠DCA … [equation (iii)]

So, from ∆BDA and ∆ADC

∠BDA = ∠ADC … [both the angles are equal to 90^o]

∠BAD = ∠DCA … [from equation (iii)]

Therefore, ∆BDA ~ ∆ADC

BD/AD = AD/DC = AB/AC

Because, corresponding sides of similar triangles are proportional

BD/AD = AD/DC

By cross multiplication we get,

AD² = BD × CD

AD² = 2 × 8 = 16

AD = √16

AD = 4

Question 14. A 15 metres high tower casts a shadow of 24 metres long at a certain time and at the same time, a telephone pole casts a shadow 16 metres long. Find the height of the telephone pole.

Answer :

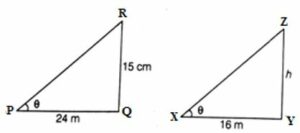
Height of a tower AB = 15 m
and its shadow BC = 24 m
At the same time and position
Let the height of a telephone pole DE = x m
and its shadow EF = 16 m

∆PQR ~ ∆MNO

Therefore, PQ/MN = ON/RQ

15/x = 24/16

By cross multiplication we get,

x = (15 × 16)/24

x = 240/24

x = 10

Hence, height of pole = 10 m.

Question 15. A street light bulb is fixed on a pole 6 m above the level of street. If a woman of height casts a shadow of 3 m, find how far she is away from the base of the pole?

Answer :

Height of height pole(AB) = 6m
and height of a woman (DE) = 1.5 m
Here shadow EF = 3 m .

Hence, pole and woman are standing in the same line

PM ||MR

∆PRQ ~ ∆MNR

So, RQ/RN = PQ/MN

(3 + x)/3 = 6/1.5

(3 + x)/3 = 60/15

(3 + x)/3 = 4/1

(3 + x) = 12

X = 12 – 3

X = 9m

Hence, women is 9m away from the pole.

—  : End of ML Aggarwal Similarity Exe-13.1 Class 10 ICSE Maths Solutions : –

Return to:   ML Aggarwal Solutions for ICSE Class-10

Thanks

Please Share with Your Friends